1. 新しい美学の方へ
今日、私たちの身の回りには、スマートフォンに組み込まれたカメラや監視カメラ、そこから得られた画像データを解析するコンピュータビジョンや機械学習技術によって、人間のためだけではない、機械やソフトウェアのような、非人間による非人間のための、さまざまな視覚的表現が現われた。こうした状況を背景に、アーティスト／批評家のジェームズ・ブライドルは、2011年5月から自身のTumblr上で、ハードウェアとソフトウェアが混在した今日のハイブリッドな社会における、新たな美学のありかとその意味を探る「The New Aesthetic（新しい美学）」という研究プロジェクトを開始した。
ここでいう「美学」が扱っているのは、いわゆる「美しいもの」ではない。伝統的に美学は、芸術作品や自然を対象に「美とは何か」という美の本質、「どのようなものが美しいのか」という美の基準、「美は何のためにあるのか」という美の価値の問題に取り組んできた。しかし今日の「美学」とは、主に芸術の意味や働きについて哲学的に考える学問であり、広く「芸術、文化及び自然に関する批評的考察」であると位置づけられている。
今日の技術、特に私たちの生活や社会、そして生命に直接かかわりのある技術の多くは、人間の目に直接触れることがない。画像のコーデック、通信のプロトコル、解析や編集のアルゴリズム、機械学習のプロセス、学習結果のデータベース、クラウドサーバー、衛星通信、インターネットの海底ケーブル —— ソフトウェアからハードウェアまで、こうした身近な技術は、私たちの目には見えないもの、つまりインヴィジブルウェアである。それと同時に、スマートフォンのカメラや監視カメラ、SNSによる情報収集、検索エンジンのクエリのように、あまりに量が多すぎて、目の前にあるにもかかわらず、いちいち人が見なく（見ようとしなく）なってしまったものも多い。
こうした見えないものの多くは、単体のモノ（オブジェクト）として存在しているのではなく、相互に接続されたシステムとして機能している。そしてこの見えないモノたちが、ネットワークで相互接続され、全体として膨大なアルゴリズム（プログラムコード）に従う高速の計算や通信を行うことで、その実行結果を環境の中に再提示する。私たちは知らず知らずのうちに、こうした見えないシステムが作り出した暗黙の再帰的環境によって、ものの見方や理解の仕方、感じ方や考え方、さらには日々の行動を変化させられている。このことを技術と人間の共進化と捉えるのか、それとも技術に対する人間の隷属と見なすのかは、技術そのものよりも、そのシステムを生み出した、あるいはそれが指し示している政治性の如何による。
「美」というのものは、いつの時代、どこの世界においても、ある種の「力」として、常に政治的な意味を伴って定義され、そのために利用されてきた。「新しい美学」が取り上げる、人間とソフトウェアのハイブリッドな生態系の共進化から生まれる美学は、表層的な色彩や形態、あるいはプロジェクターやセンサーの技術的問題にとどまるものではない。重要なのは表現や技術それ自体ではなく、それらが指し示している意味とその使用法なのだ。
知覚、そして美学のポリティクスはいつの時代にも潜在、遍在している。新しい美学を特徴付けている、グリッチやバグによる「失敗の美学」、あるいはビットマップやローレゾによる「解像度の美学」は、実現や成功の政治性、見えることやわかることの政治性を浮き彫りにする。こうした科学技術の権威的な美学＝政治性を指摘できなければ、私たちは逆に、科学技術に消費されるだけの存在になってしまう。
また「美学」というタームには、政治性以外にも、さまざまな歴史的、文化的な意味や文脈がある。だからこそ、科学や技術が人や機械に新しい知覚や環境を提供し続けている限り、文化や歴史に強い影響を与える（美学の）政治性を常に批判し、議論し続けていく必要がある。
2. 機能としての美学
ある対象（オブジェクト）について考えられてきた、芸術的な意味の総称としての「美」が、この「新しい美学」のように系（システム）全体に着目するようになった時、この「システムとしての美学」とは、いったいどういうものになるのだろうか。僕は、その構造が「機能」と同じであると考えている。
機能とは、ある特定の時空領域に含まれる物質情報系の相互作用において、ある「意味」のもとに抽出された現象の連鎖のことを指す。ここで対象と協働して、機能＝意味を提示する者を「使用者」と呼ぶことにすれば、例えば道具の機能は、常にそれを使う使用者と対で現れる。逆にいえば、この観測者としての「使用者」の意図や能力に応じて、道具の機能が出現する。
「新しい美学」が、この機能と同じ構造を持っているとすれば、「新しい美学」とは、芸術的な意味を生み出す芸術的対象（芸術作品）とその鑑賞者（芸術的使用者）の対生成（励起）とその対消滅（脱励起）を生み出す構造が、外部環境と相互作用しながら時間発展的に変化していくメカニズムである。いいかえれば、芸術作品とは、この外部環境系との相互作用の中で、鑑賞者が意味を見い出すことができるものとして定義される。機能と環境系との関わりの様相は、何らかの相互作用によって系の状態が変化しながらも、その構造が保たれる「非平衡開放系」のシステムである。この芸術と環境系の関わりの様相は同様のシステムと見なすことができ、広く「アートワールド」とも呼ばれている。
3. 芸術的活動の素過程
堀裕和はこうした機能の本質的構造を、図式によってその動的関係を明快に表現できる圏論を用いて、数理的に描写した。圏論は、ある対象を調べる際に、対象の具体的な中身を考えるのではなく、その器の性質の関係と引き継がれる構造に焦点を当てる。そうすることで、構造を保つものごととその関係性を、抽象的かつ厳密に扱うことができる。掘のモデルのポイントは、圏論やホモロジー代数を利用して、「来歴を変化させながら構造を保って進化する図式」を導出し、機能の本質を描写したことにある。
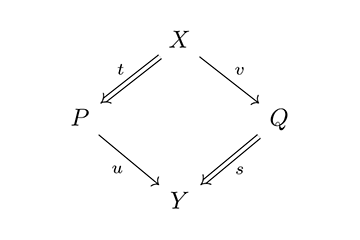
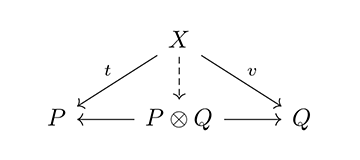
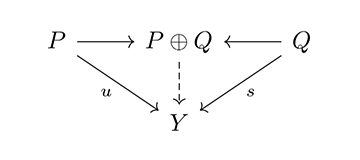
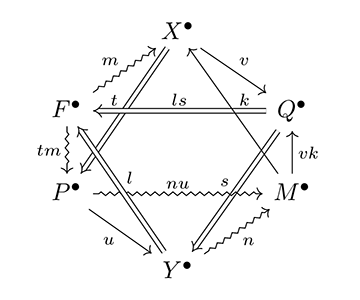
堀が示した圏論による機能の数理的描写を応用して、2017年に僕らは「新しい種類の美学（A New Kind of Aesthetics）」を提唱した。そこでは前述のように、美の構造は機能の構造と同じである、という仮説を出発点に、芸術的対象とその鑑賞者の対生成（励起）と対消滅（脱励起）のシステムを、直積（励起）と直和（脱励起）という圏の図式（可換図式）で表現した。可換図式とは、［図1］で X, P, Q, Y からなる四角形の圏の図式のように、始点からのすべての射の合成が同じ終点を持つ図式のことである。
§
| P | 鑑賞者 |
| Q | 芸術的対象 |
| X | 芸術概念 |
| Y | 芸術的状態 |
［図1］
［図2］
［図3］
鑑賞者としての主体 P と、芸術作品としての対象 Q の関係をもたらした隠れた要因 X を「芸術概念」に、その関係が生み出した像 Y を「芸術的状態」に対応させる。［図1］は、直積［図2］と直和［図3］を持つ加法圏の積閉系の考え方にしたがっている。つまり、X は P, Q の関係を生み出す破線の射を一意に定めるような要因を表わし、その P, Q の関係から生まれる破線の射を一意に定めるような状態として Y という結果が得られることになる。
この図式において、鑑賞者 P と芸術的対象 Q を生み出す射 t と s の選択には、蓋然性と多様性があるが、その多様な分解を同一視する同値な積閉系の関係は、常に隠れた要因 X に支配されている。すなわち芸術概念 X とは、鑑賞者と芸術的対象が共同で生成している非自明な芸術世界の全体を指している。このとき鑑賞者 P と対象 Q の関係は、X の像としての芸術的状態 Y から推測することができる。
4. 環境系の導入
ここで提案する芸術モデルの特徴の一つは、こうした鑑賞者と芸術作品の系だけでなく、それを取り巻く環境系を導入することにある。ここでいう環境とは、著名な芸術家や批評家、学芸員や美術商といった一定の権威を有する社会集団による、いわゆる「アートワールド」だけではなく、鑑賞者が芸術作品と共に作り出す意味を支える、社会的、政治的、文化的、科学技術的な背景（文脈）全般に相当している。
まずはじめに、ある芸術的対象 Q を生成する要因 M を考える。M は、それを拡張した芸術的概念 X を介して、絵画や彫刻、音楽や詩といった、多種多様な芸術作品 Q とその鑑賞者 P を対生成するものとする。［図1］において、M は v : X → Q の核であり、M = Ker(v) と表現できる。核 M とは、v によって 0（関係のないものごと）に写像される射 k : M → X として定義され、Q においては 0 に写像されて見えなくなるため、Q の環境と呼ぶことができる。
次に、人工物や自然といった様々な芸術的対象 Q から生まれた芸術的状態 Y が、Q の性質や特徴毎に分析された結果となる F を考える。F は、芸術的対象 Q と s によって発生した芸術的状態 Y を、要因 Q と s によって仕分けたものであり、鑑賞行為の分析結果を意味している。［図1］において、F は s : Q → Y の余核であり、F = Cok(s) と表現できる。余核 F とは、s の終域 Y における s の像による商対象 Y/Im(s) と定義され、要因 Q と s が仕分けの基準となることで見えなくなっているため、これも Q の（次のステップにおける）環境と呼ぶことができる。
この2つの環境系を［図1］に導入すると、［図4］のように書くことができる。
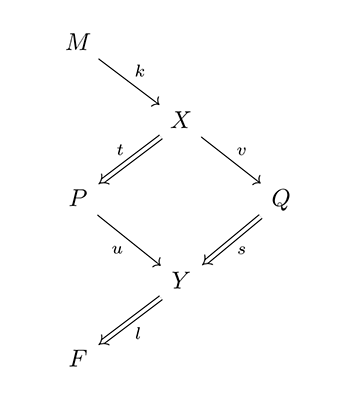
| P | 鑑賞者 |
| Q | 芸術的対象 |
| X | 芸術概念 |
| Y | 芸術的状態 |
| M | 芸術的対象の生成要因 |
| F | 芸術的状態の分析結果 |
［図4］
なお、この M → X → Q と Q → Y → F のことを、短完全列という。以下の［図5］のような短完全列とは、Im(f) = Ker(g) （射 f の像が次の射 g の核と一致する）、f が単射で g が全射となる完全系列のことを指す。
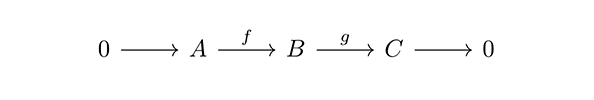［図5］
このとき、C = B/A すなわち、C は B の余核となっている。Im(f) とは、B の中で A の影響を受けている部分であり、それが Ker(g) と等しいということは、A の影響が C にいくと見えなくなってしまうことを意味している。つまり Ker(g) は B の一部で C に直接影響を与えない部分である。また、A は A ではないものごとである左端の 0 で決まり、右端の 0 は、A が C の仕分けの基準になっていることを示している。
短完全列が意味しているのは、芸術的概念 X の多様な内容が、芸術的対象 Q = X/M に「同じものごと」として写され、それが芸術的対象の生成要因である M に含まれる「ものごとの種類」で区分けされている、ということである。直接には把握できない種別の要因 M は、Q における分類に基づいて特定され、名付けられている。同様の関係が、芸術的対象 Q の多様な拡張として生まれた芸術的状態 Y と、それを Q と s によって分類した芸術的状態の分析結果 F の間にも成り立っている。
さらに射 u : P → Y を鑑賞行為としてとらえた時、(u, s) という射の組み合わせが、鑑賞者と対象の関係の開示のされかた、すなわち「芸術的行為の性質」を決定づけ、このことから芸術的活動のダイナミックスに係る理解が得られる。同時に (v, t) という射の組み合わせが、(u, s) という射の組み合わせと（前述の可換図式において）共形なので、鑑賞者と対象の関係が、「芸術的行為の性質」に基づいて X から開示される。
5. 時間の導入
芸術的行為には環境系としての背景や文脈だけでなく、時間軸、すなわちそのダイナミックな時間発展が重要である。どのような芸術的対象や行為であっても、その関係（意味や価値）は時間や時代の中で変化し続けている。そこで、環境系に続いて、ホモロジー代数における複体の概念を用いて、時間をモデルに導入する。複体とは、2つ続けて写すと 0 になる準同型射 (∂n∂n−1 = 0) で接続された対象の連鎖 Cn であり、これは C● = (Cn, ∂n) という、限りなく続く図式［図6］で表される。
［図6］
このとき時間は、前述の短完全列［図5］が平衡に達するのに必要な持続から生まれる。ステップ毎の時間発展の来歴は、局所環境を入れる器としての複体 C● の n 次のコホモロジー Hn(C●) = Ker(∂n)/Im(∂n−1) に記録される。コホモロジーとは、Cn−1 の像の局所環境による補足であり、それが Cn+1 に影響を与えない（2つ続けて写すと 0 になる）ということは、コホモロジーが Cn の本質であることを示している。つまり、このコホモロジーを含む圏の図式には、芸術に直接関係する鑑賞者や作品だけに限らない、社会や技術といった環境系からの非自明な影響が記録されている。
ホモロジー代数を展開するための舞台として活用されるアーベル圏においては、この複体もまた対象であり、短完全列を構成することができる。このとき複体の射は f : C● → D●(fn : Cn → Dn) , fn−1∂n = ∂nfn で定義される。すると、鎖（チェイン）ごとに完全な複体 0 → A● → B● → C● → 0 は、すべての次数で短完全列 0 → An → Bn → Cn → 0 を保ち、各複体 An, Bn, Cn が、来歴 Hn(A●), Hn(B●), Hn(C●) を包含し発展する時間構造の基本図式［図7］を与える。
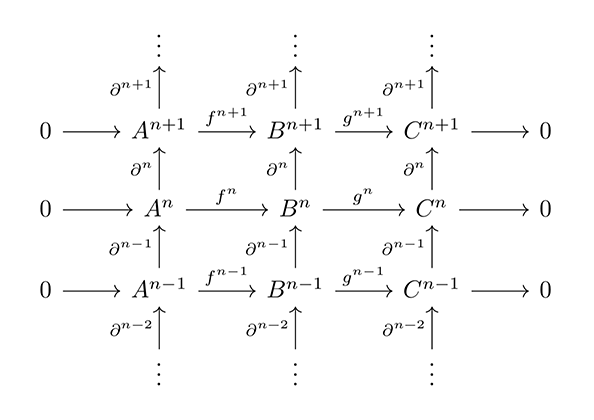［図7］
ホモロジー代数における「ヘビの補題」によって、準同型射のみで構成される鎖ごとに完全な複体から、コホモロジーの長完全列［図8］が導かれる。ここでコホモロジー Hn の次元を一つ上げる射 Hn(C●) ⇝ Hn+1(A●) は、連結射と呼ばれる。
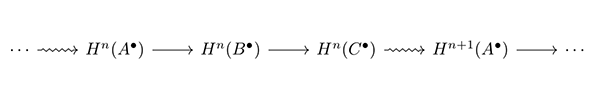［図8］
このことは、鎖ごとに自明な複体の図式の背景で、対象の連鎖を支える共通の土台である環境系（コホモロジー）が、非自明で見えないものごとを含む、時空間的連鎖を維持していることを示している。
6. 三角圏と八面体構造
圏の任意の射が余像と像を持ち、完全列と同じように、その余像と像が同型となるとき、それを完全圏という。加法圏の一種であるアーベル圏も、完全圏の一つである。完全圏の射 f の機能は、余像と像の関係が同型 Coim(f) ∼ Im(f) となる過程を経て、そこまで来たものごとを完全に消滅させ、そこから続くものごとを生成する。
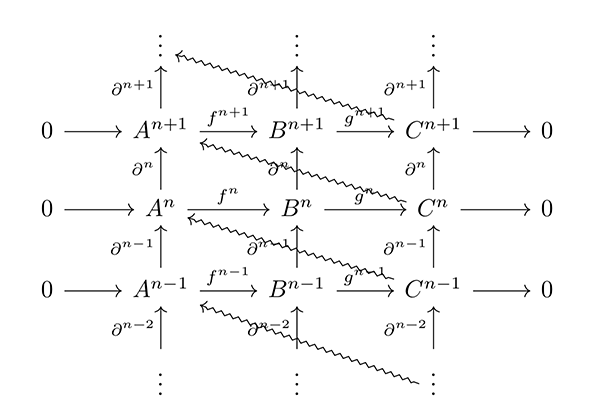
位相同型でものごとの連鎖が議論でき、それが分裂完全列である場合には、アーベル圏のホモトピー同値を用いて、コホモロジーの長完全列［図8］の図式を、複体の接続関係として［図9］と［図10］のように図式化することができる。複体を対象の連鎖ではなく、列のまままとめて扱う導来圏として構成される三角図式のことを、三角圏と呼ぶ。この時、将来の環境のホモロジーを無視することで、そこまでのコホモロジーに入った Cn の来歴と Cn を擬同型として同一視することができる。
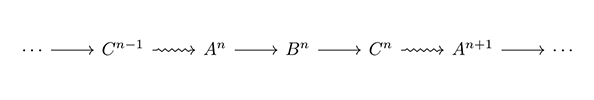［図9］
［図10］
ここで波型矢線で示した「複体を1階層上げる射」が、［図8］で示した長完全列の連結射である。この複体の三角図式（三角圏）は、来歴を変化させつつも、構造を保って進化する対象の簡明な表現となっている。
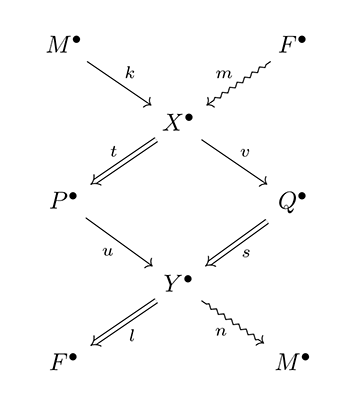
そこで可換図式［図4］の対象を複体に置き換え、それをこの三角圏を用いて拡張する。まず、連結射で結ばれる1ステップ前の芸術的状態の分析結果 F● と、1ステップ後の芸術的対象の生成要因 M● を加えると［図11］のようになる。
［図11］
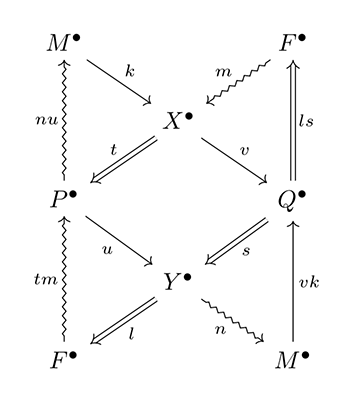
ここからさらに、自然に導かれる射 Q● → F●, M● → Q●、そして連結射 F● ⇝ P●, P● ⇝ M● を補うと、［図12］と［図13］の図式が得られる。
［図12］
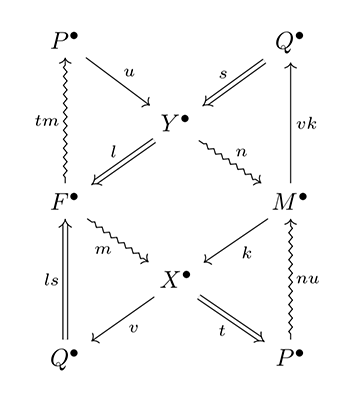［図13］
この図式の階層の異なる環境 M● と F● を貼り合わせると、以下の1つの可換図式と4つの三角圏から構成される八面体［図14］が構成される。
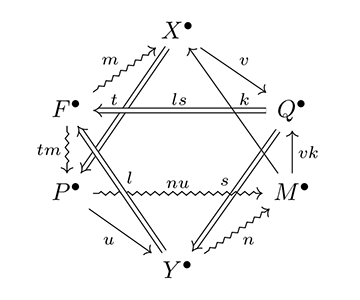
| P● | 鑑賞者 |
| Q● | 芸術的対象 |
| X● | 芸術概念 |
| Y● | 芸術的状態 |
| M● | 芸術的対象の生成要因 |
| F● | 芸術的状態の分析結果 |
［図14］
7. 芸術的活動とその時間発展
この八面体は、八面体公理と呼ばれる、導来圏の重要な帰結の一つに相当する。ここに含まれる4つの三角圏を詳しく見ていくと、それぞれが芸術的活動における「芸術の思索」「作品制作」「芸術の経験」「作品分析」に相当していると解釈できる。つまり、この八面体構造は、こうした芸術的活動に関連するさまざまなものごとが、相互に関連し合いながら時間発展していく様子を、数理的に描写したものである。
芸術の思索
芸術的対象の要因 M● → 芸術的概念 X● → 鑑賞者 P● → 芸術的対象の要因 M●
作品制作
芸術的概念 X● → 芸術的対象 Q● → 芸術的状態の分析 F● → 芸術的概念 X●
芸術の経験
芸術的対象の要因 M● → 芸術的対象 Q● → 芸術的状態 Y● → 芸術的対象の要因 M●
作品分析
鑑賞者 P● → 芸術的状態 Y● → 芸術的状態の分析 F● → 鑑賞者 P●
また、この4つの完全系列としての芸術的活動の関係を［図15］のように記述することで、八面体構造の組紐構造と呼ばれる、各対象（複体）の相互関係が明確になる。
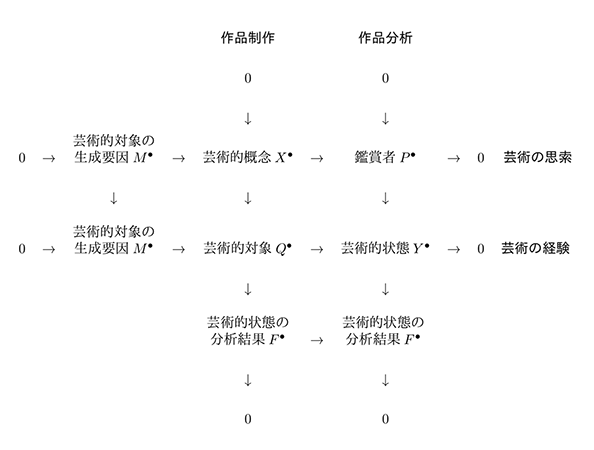［図15］4つの組紐構造としての芸術的活動
最後に再び、冒頭の積閉系による可換図式［図1］に立ち返る。(P, Q) を二つの対象の単純な和とすると、X → (P, Q) → Y は短完全列と同じように、要因 X とそこから拡張された多様な現象 (P, Q) 、およびこれを要因で整理した Y という意味を持つ。さらに環境系を導入した［図4］を参照すれば、可換図式に囲まれたものを除く全てである環境系の組 (F, M) が、この可換図式の時間発展の構造を支えていることがわかる。その過程で (P, Q) は環境系の特異性をステップ毎に取り込み、非自明な来歴を獲得していく。特異性を取りこむ毎にコホモロジーの次元は上がり（ホモロジーの次元が下がり）、その構造は簡単になっていく。すなわち、最初は曖昧で不可知な芸術的概念 X が、芸術的対象 Q と鑑賞者 P から生まれる芸術的状態 Y によってその性質を少しずつ特定されることで、次第に明確になっていくことを示している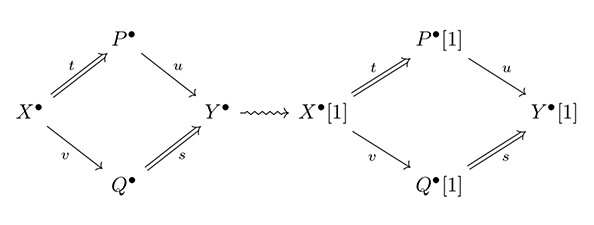［図16］。
［図16］
8. 芸術的活動の普遍性
1957年4月に開催されたアメリカ芸術家連盟の総会で、芸術家のマルセル・デュシャンは「創造過程（The Creative Act）」という講演を行った。日本語訳は、北山研二の訳によるものが書籍化されている。
ここでデュシャンは、創造的行為において鑑賞者の鑑賞行為が、芸術的活動における作者の制作行為以上に重要な意味を持つとして明確に評価した。特に、（作者が）「個人的に意図しながら表現されなかったもの」と「意図せず表現されたもの」との間の関係を「芸術係数」と呼び、この違いの重要性を指摘した。その上で、創造的行為というものが、近代性の中で特権化された個人としての作者だけで完遂されるものではなく、作品に内在する質を翻訳し、解釈するオープンな鑑賞者によって、作品と外部世界とのつながりが生まれることを、講演の最後に述べている。
要するに、芸術家は一人では創造行為を遂行しない。鑑賞者は作品を外部世界に接触させて、その作品を作品たらしめている奥深いものを解読し解釈するのであり、そのことにより鑑賞者固有の仕方で創造過程に参与するのである。こうした参与の仕方は、後世がその決定的な審判を下し何人かの忘れられた芸術家を復権するときに、一層明らかになる。マルセル・デュシャン「創造過程」
今回の芸術的活動のモデルは、このデュシャンの創造的行為の構造を描写したものでもある。本モデルの対象の中には、「作者」というものが明示されていない。その代わりに、（しばしば芸術作品と呼ばれる）芸術的対象と鑑賞者の対生成と対消滅が、そのダイナミズムとディメンジョン（スケール）の基盤となっている。この可換図式には、環境系の特異性を取り込むことで、非自明な来歴を獲得する構造が秘められている。この図式をその要因（核）と分析結果（余核）で拡張することから導かれる、公理としての八面体構造の時間発展を通じて、デュシャンのいう鑑賞者と作品の対と、外部世界（環境）のつながりが生成されていく。
芸術的行為にとって「作者」というものは、単なる個人ではなく、個人を形成する環境（社会、歴史、心理、哲学など）と切り離すことができない。さらに今日では、作者が人間ではなく、コンピュータソフトウェアのような広義の（実行可能な）「テクスト」とその（実行）環境にまで拡張している。（人工知能や人工生命を含む）ソフトウェアもまた、ロラン・バルトが「作者の死」で述べたような、現在・過去の文化の引用からなる多元的な「織物」であり、ソフトウェア・アートのように、その実行結果が芸術的対象となることもある［図17］。
| P● | 鑑賞者 |
| Q● | ソフトウェアの実行結果 |
| X● | ソフトウェアの実行状態 |
| Y● | 実行結果の鑑賞状態 |
| M● | プログラムコード |
| F● | 鑑賞状態の分析結果 |
［図17］
本稿の冒頭で紹介した、ジェームズ・ブライドルの「新しい美学」とは、今日の文化を特徴付けている実行可能なテクストとしてのプログラムが生成する対象と、そのテキスト（ソフトウェア）を書き、その結果を思索体験する人間のハイブリッドが織りなす、環境とのダイナミズムであるといえる。
導来圏の八面体構造は、実際には極めて複雑なものごとの関わりから構成され、数学の力を借りずには導出困難な構造ではあるが、その結果は極めて明快であり、ものごとの機能や芸術的活動だけでなく、さまざまな現象や行為に適用することが可能な普遍性を有している。なぜならこの図式は数学的公理であり、それはある特定のものごとの記述のための道具ではなく、この図式のようにふるまうものごとが、共通の土台である環境系を通じて暗黙のうちに絡み合いながら生成発展していくという、この宇宙における普遍的な動的構造を表現しているからだ。
特にここで用いた導来圏は、ホモロジー代数（チェイン複体）を定義できるアーベル圏において、以下の操作で構成される。
- 関係ないものごと（0の同値類）を無視する
- 積閉系の自由度に基づいて都合のよい尺度からものごとを表象する
- ホモトピー同値で似たような射を同一視する
- 擬同型でものごととその来歴を同一視する
これらは、私たちが日常、環境系の様相を捉え様々な判断や評価を下す際に自然に行っている、省略や捨象選択に基づくものごとの把握の仕方や、限られた情報から様々なことを補ってものごとを進めていく行為の特徴を、良く（というよりも見事に）捉えていることに、僕は感嘆せざるを得ない。圏論という、あいまいなものごとを厳密に取り扱うことができる数学的言語が持つ、領域を超えた深い描写力の可能性を、引き続き探求していきたい。
