コンピュータ・アートとは何か?それはコンピュータの芸術である。芸術活動の主体はコンピュータである。……我々の目指すコンピュータ・アートとはコンピュータを芸術創造の主体とするコンピュータのアートであり、コンピュータが芸術するのであって、コンピュータを利用する人間芸術とはその理念を異にするものである。
コンピュータはプログラムなるものを記憶内蔵し、その内なる指令を解釈して自動的に情報を処理(計算)をする、言うなれば脳を模した機械であり、その一切の動作はプログラムによって実行される。ゆえにこの内蔵プログラムの中身が芸術創造に関する指令系をなしているならば、コンピュータはこのプログラムに従って自発的自律的に芸術活動ができ、その結果作品を創り出すことになる。このようなプログラム主導の芸術を我々は真正コンピュータ・アート(コンピュータの芸術)と呼ぶ。
川野洋「コンピュータ・アートとは何か」※1
はじめに
コンピュータを芸術活動の主体とする「コンピュータアート」にとって、量子計算、そして量子コンピュータの出現はどのような意味を持つのだろうか?
コンピュータアートの中核にあるのは、数と計算やアルゴリズムの振る舞いである。コンピュータの計算の手続きをアルゴリズムといい、そのアルゴリズムをコンピュータが実行できる形式で記述したものがプログラムコードである。プログラムコードが実行するアルゴリズムの出力を人間が知覚し、アルゴリズムそのものと相互作用することによって、芸術的な鑑賞体験が生まれる。古典コンピュータアートにおいて、計算は確定的な数によって記述され、アルゴリズムはその明示的な演算を記述したプログラムコードによって表現されていた。同様に、アルゴリズムとその出力は、形状や色彩、あるいは動きや音響のような、人間が知覚可能なものとして提示されていた。
数とビット
古典デジタルコンピュータが扱うデータの最小単位を「ビット」という。1ビット毎に、通常は「0」と「1」の2通りの状態を記述できる。古典コンピュータは、この2状態系のビットが表現する情報の枠組みの中で数と計算、アルゴリズムやコードを考えてきた。そこで仮定されていたのは、以下のような古典的な素朴実在論に根差した物理量の概念である※2。
- すべての物理量は、どの瞬間にも、各々ひとつずつ定まった値を持っている。
- 測定とはその時刻における物理量の値を知る(確認する)ことである。
- ある時刻における物理状態とは、その時刻におけるすべての物理量の値の一覧表のことである。
- 時間発展とは、物理量の値が時々刻々変化することである。
この物理量の値をビットで表現された数値に対応させれば、それはそのまま、今日普通に了解されているコンピュータ内の状態や計算に対する仮定となる。この人間スケールの素朴な直観に合致し、迷わず数値化できるビットの枠内で表現できる、芸術作品の形式や意味、可能性や限界を議論してきたのが、これまでのコンピュータアートの創作と批評であった。
量子論における実在
しかし20世紀に生まれ、今日広く発展した量子論は、こうした古典的実在論とは大きく異なる世界観を提示する。それは具体的には、以下のようなものである※3。
- すべての物理量が、各瞬間瞬間に定まった値を持つことはない。
- 各々の物理量は変数ではなく、演算子(線形変換)で表される。
- 物理量の測定とは、観測者が測定値をひとつ得る行為であり、一般に測定の度にばらつく。
- ある物理量の測定値の確率分布は、あるひとつの物理状態から一意に定まる。
- 物理状態とは、各物理量に対して、それを測定したときの測定値の確率分布を与えるものである。物理状態は物理量から確率分布への写像である。
- 時間発展とは、測定を行う時刻によって、異なる確率分布が得られるということである。
つまり量子論において、物理量とは測定可能な可観測量のことであり、その状態は測定値の確率分布として与えられる。
ここで、
- ψ:物理状態
- A:物理量
- a:測定値
とすれば、ボルンの確率規則により測定値の確率分布 {P(a)} は、
{P(a)} = ψ(A)
と物理状態 ψ と物理量 A の関数として表すことができる。量子論とは、これが自然の本性であるという立場から、 {P(a)} を ψ と A から計算する理論体系のことである。
量子ビット:重ね合わせともつれ合い
量子論によって得られた、古典論に替わる自然の描像から、新たな計算の概念が生まれる。それは、前述の古典的な2状態系であるビットを、量子ビット(キュビット)と呼ばれる、量子状態系に置き換えたものである。従来のビットが
- 「0」あるいは「1」のどちらかの値をとる。
- それぞれのビットの値は、他のビットの値とは関係なく定められる。
- ビットの値を他のビットにコピーすることができる。
という特徴を有しているのに対し、量子ビットは、2つの独立な量子状態から構成される、以下のような系として定義される。
- 2つの独立したビットの量子状態(基底状態ベクトル)を |0⟩ と |1⟩で表す。
- 1つの量子ビットは |ψ⟩ = α|0⟩ + β|1⟩ という状態ベクトルの線形結合で表される。
- ここで α と β は、|α|2 + |β|2 = 1 を満たす複素数である。
- 観測の結果、 |0⟩ か |1⟩ のどちらかの値が得られる。
- 観測することで、|0⟩ が得られる確率は |α|2、|1⟩ が得られる確率は |β|2 である。
重要なのは、量子ビットにおいて、観測するまでは |0⟩ の状態と |1⟩ の状態とが「同時に重なりあって存在し得る」ことである ※4。
量子ビットの第一の特徴は、この重ね合わせの状態が存在することである。同時に、未知の量子状態を複製(増殖)する事が出来ないという「量子複製不可能定理」が導かれる(その逆演算である、未知の量子状態の消去も不可能である)。古典ビットによるデジタルデータの第一の特徴が、劣化なき複製にあったことを考えると、ここに量子情報と古典情報の大きな違いがある。
さらに重ね合わせの状態にある量子ビットは、互いに独立でない(個別の量子状態に分離できない)ペアを作ることができる。これを「量子もつれ(エンタングルメント)」という。もつれ合いの状態にある量子ビットは互いに強い相関をもち、ある一方の量子ビットを観測すると、もう一方の量子ビットの状態が、たとえ空間的にどんなに離れていたとしても、ただちに影響を受ける。量子もつれの関係にある2つの量子ビットを用いれば、量子状態を離れた場所に転送することができる(量子テレポーテーション)。
「ある地点で行われた行為や起こった現象によって、遠くの実験結果がただちに変わることはない」古典物理学では説明不可能な、この量子ビット間のもつれ合いによる相関のことを「量子力学の非局所性」という。古典ビットによる従来のコンピュータが、先述の素朴実在論と局所性を仮定した物理学にもとづいていたのに対し、確率的で非局所的な量子論による量子ビットを用いた計算を実行する計算機が、本稿が対象とする「量子コンピュータ」である。
量子回路
量子コンピュータが計算を実行するときに用いる手続きの代表例は、量子ゲートとそれらを組み合わせたゲート型と呼ばれる量子回路である※5。量子回路とは、どの量子ビットにどの量子ゲート(古典コンピュータにおける論理ゲートに相当する)を、どのような順序で適用するか、という手順を示すもので、この量子回路が量子ビットを操作するプログラム、つまり量子アルゴリズムを記述したものになる。
量子ゲートの特徴は、その入力数と出力数が常に等しいことにある。量子計算は、|0⟩ と |1⟩ という2つの基底状態を持つヒルベルト空間(任意次元の複素線型空間)内の操作に限られるので、その計算は可逆でなければならない。
1量子ビットに対してユニタリ変換(2つのベクトルの内積の値が変わらないような変換)を施す「ユニタリゲート」にもさまざまなものがあるが、重ね合わせの状態を作り出す「アダマールゲート(H)」と、位相を π/4(45度)回転させる「Tゲート(T)」、そして2量子ビット操作の「制御NOTゲート(CNOT)」があれば、いかなる量子計算も可能になる(万能量子機械)。CNOT は、ある一方の入力(制御ビット)が |1⟩ のときのみ、もう一方の入力(標的ビット)を反転する。ここで反転とは、「NOTゲート(X)」の操作をすることに相当し、この操作によって2つの量子ビットのもつれ合いを作ることができる。
- アダマールゲート(H):重ね合わせを作り出す(X-Z 軸周りに π 回転)
- Tゲート(T):位相シフト(Z 軸周りに π/4 回転)
- NOTゲート(X):ビット反転(X 軸周りに π 回転)
- 制御NOTゲート(CNOT):もつれ合いを作り出す(制御ビットが |1⟩ のとき、標的ビットをビット反転)
これらの量子ゲートによって操作された量子ビットに対して、測定ゲートを適用することで、量子情報を古典情報にして観測する。量子コンピュータは、こうしたさまざまなゲートを用いて、
- 量子ビットという複素数で表現される物理状態を用意する。
- 量子ビットにゲート演算を施して以下のような操作をする。
- 量子ビットの状態を変化させる(重ね合わせ状態を作り出す)。
- 複数の量子ビットがもつれ合う状態を作り出す。
- 量子ビットを測定することで、計算結果を確率的に得る。
- 計算と測定を繰り返し実行することで、測定値の統計的な分布を得る。
という手順で量子計算を実行する。従来のコンピュータアートが古典計算による計算芸術であったとすれば、多くの情報を重ね合わせた状態のまま計算する量子計算とそのアルゴリズムによる計算芸術が「量子コンピュータアート」である。
量子プログラミング
次に具体的な量子プログラムを見ていきたい。量子アルゴリズムを記述する量子プログラミング言語にもさまざまなものがあるが、ここでは、IBMが開発しているオープンソースのPythonライブラリである「Qiskit(キスキット)」と、それを実行できる「IBM Quantum Composer」を用いる※6。
量子コンピュータの「Hello, World!」プログラムと呼ばれているのが、次の量子回路である。
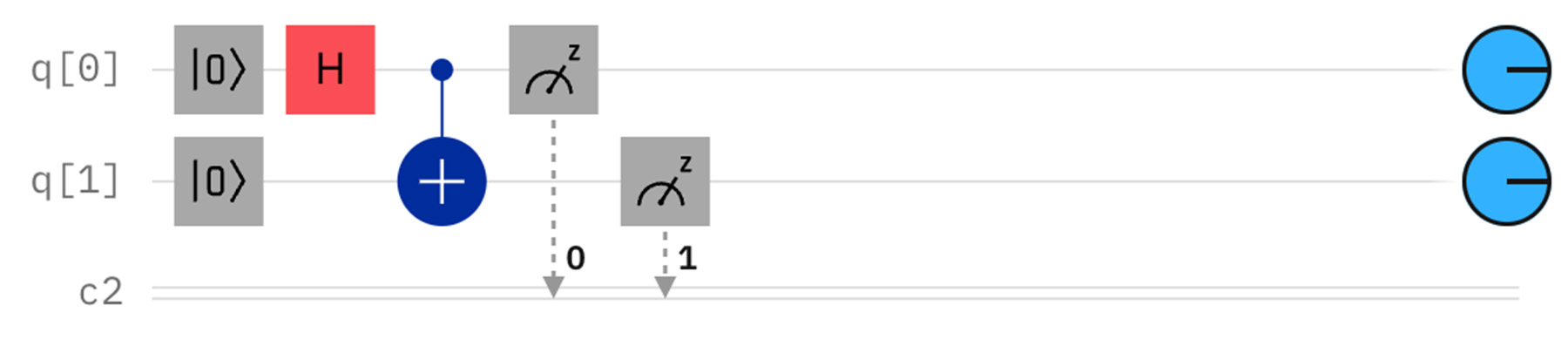
この量子プログラムは、q[0]とq[1]という2つの量子ビットを用意して初期化したあと、 q[0] にアダマールゲートを適用して重ね合わせ状態(Bell状態)にする。次に q[0] を制御ビット、 q[1] を標的ビットとして、制御NOTゲートを適用する。すると、 q[0] と q[1] がもつれ合い状態になる。
この重ね合わせともつれ合い状態にある2つの量子ビットを1024回測定すると、以下のような結果になる。
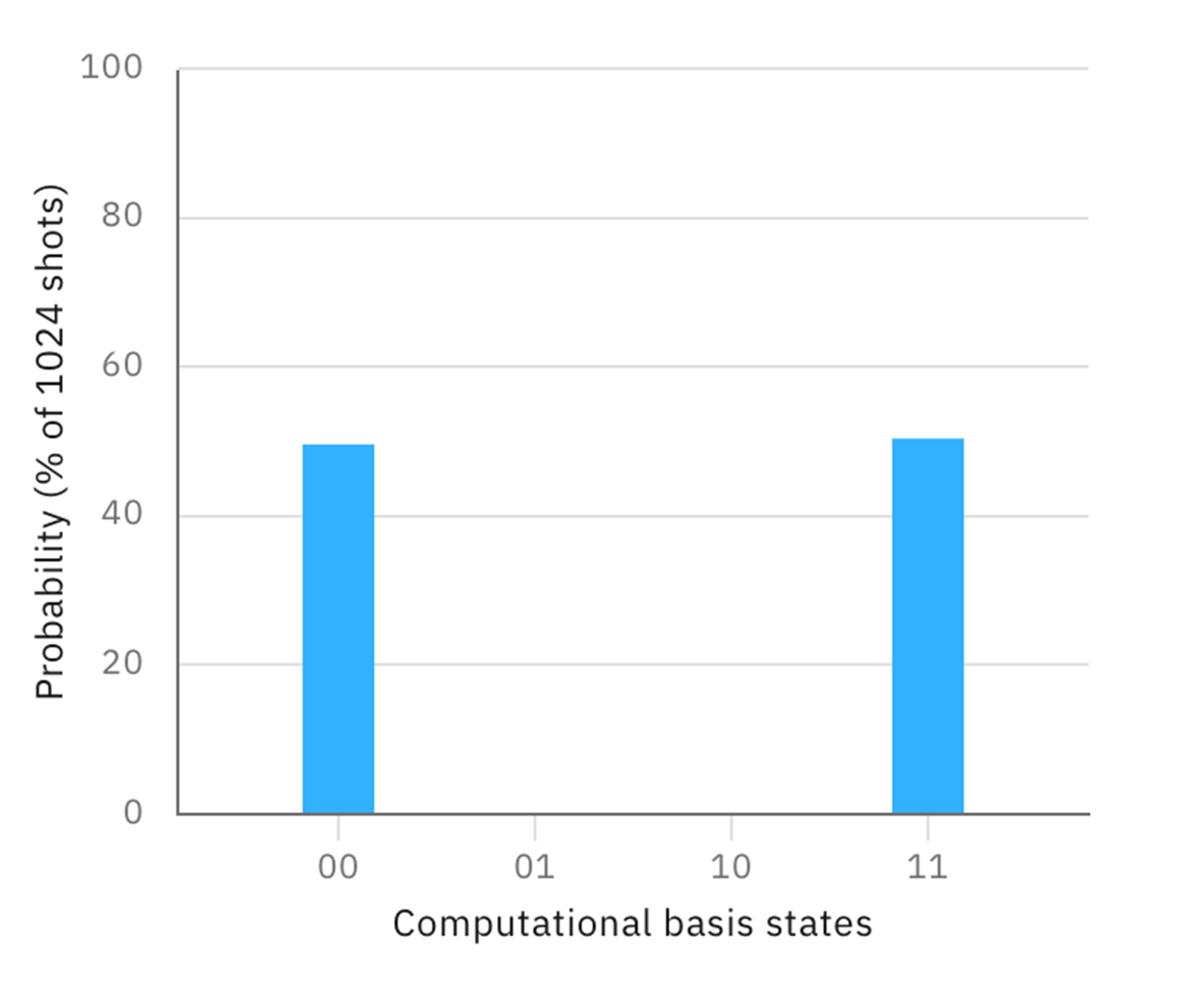
横軸は2つの量子ビットを測定した結果で、左側の最初の桁がq[1]、右側の桁がq[0]の測定結果である。重ね合わせの状態にあることから、それぞれの量子ビットの測定結果は、0と1>が半々、つまり等しい確率で現れる。さらに2つの量子ビットがもつれ合いの状態にあることから、q[0]が0であれば、q[1]も必ず0になり、q[0]が1であれば、q[1]も必ず1になる。この短いプログラムの中に、重ね合わせともつれ合いという、量子計算の2つの核心が含まれている。
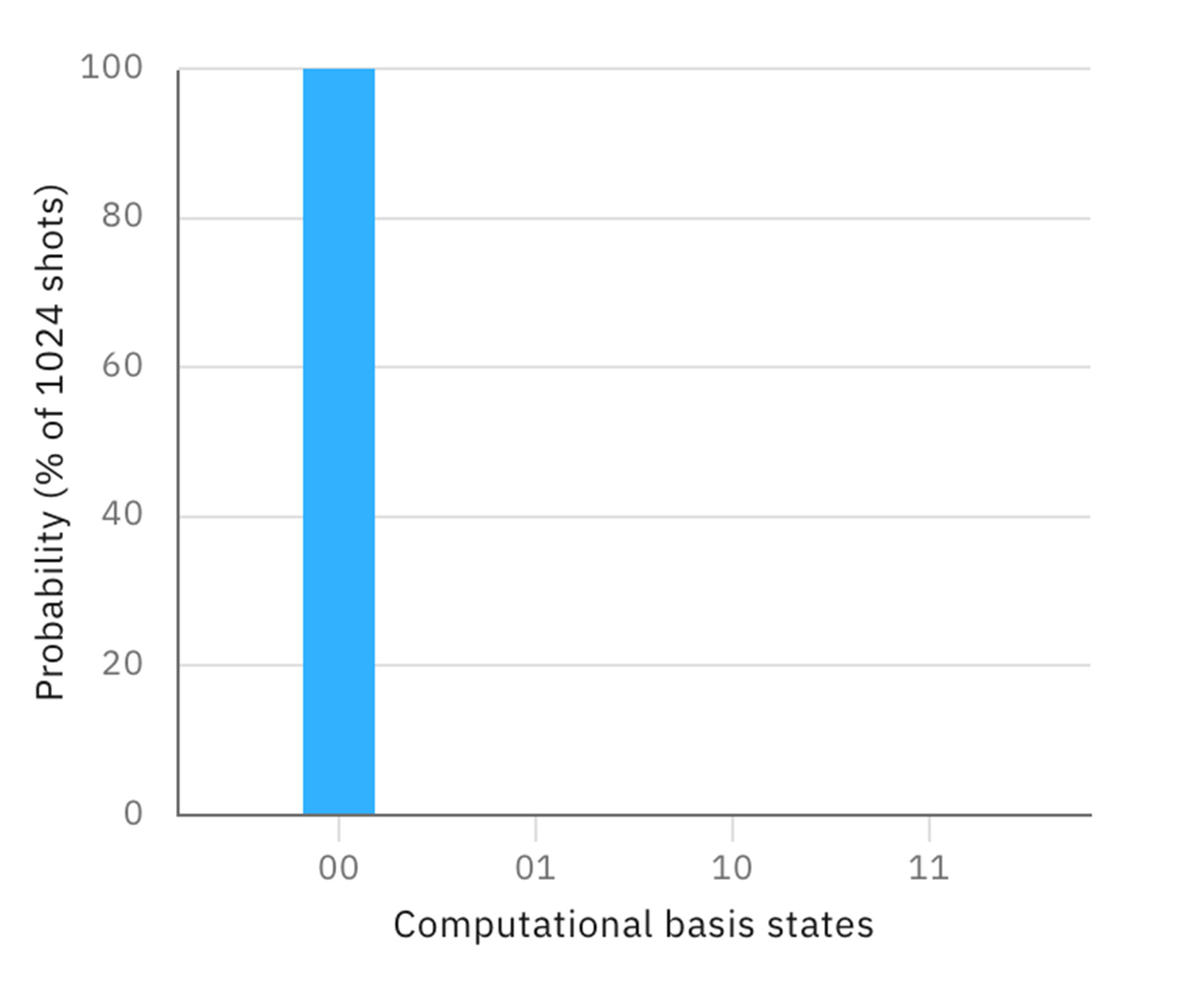
例えば、以下の量子プログラムは、 q[0] を重ね合わせ状態にせず、 |0⟩ のまま制御NOTゲートを適用したものである。

この場合は、単純に制御ビット q[0] の測定結果は常に0で、標的ビット q[1] には何もしないので、同じく常に0となる。これは2つの古典ビットを用いた論理計算の結果と同じである。
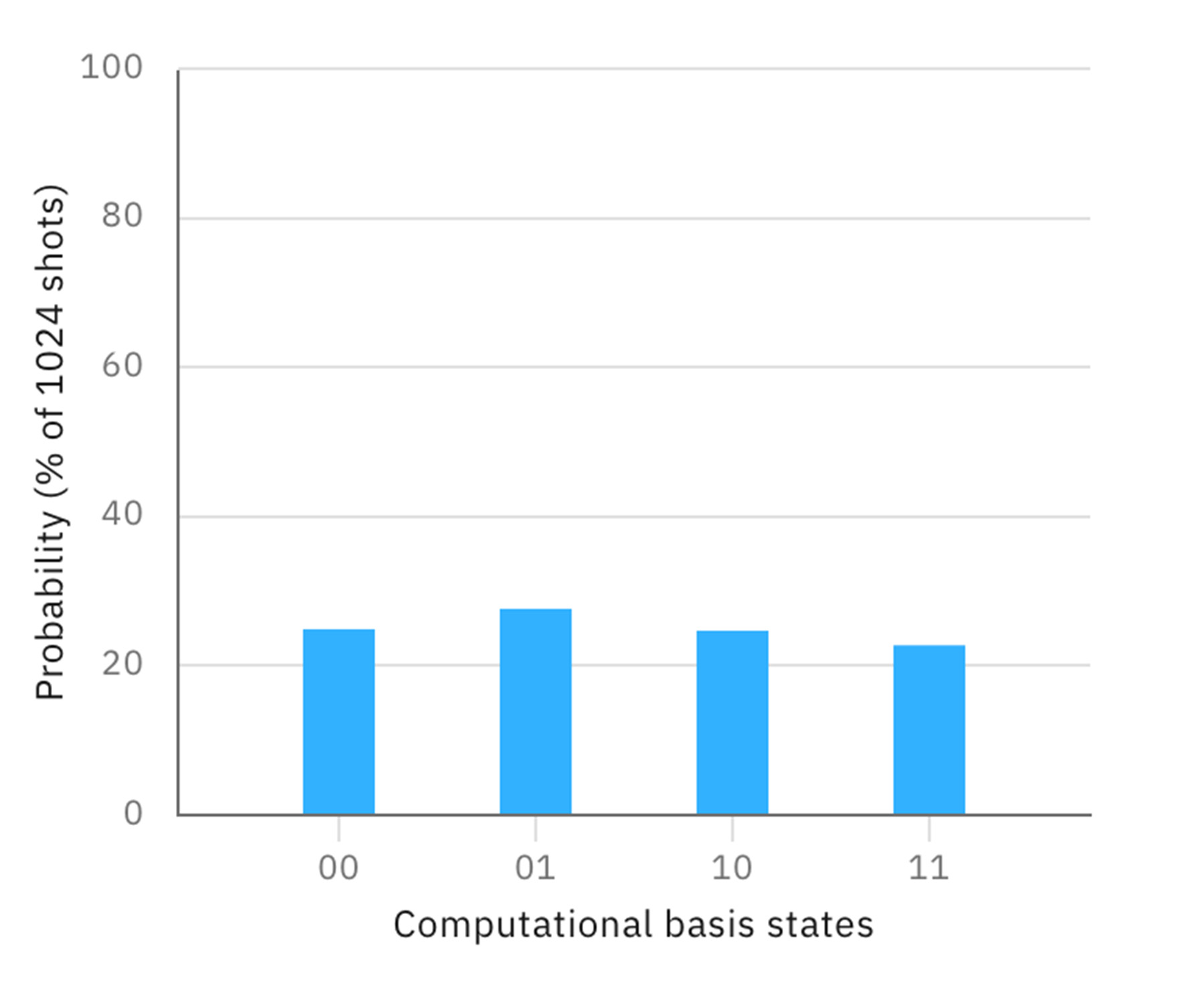
次に、2つの量子ビットを共に重ね合わせの状態にしたあと、制御NOTゲートを適用せずに、つまりもつれ合わせずに測定してみる。

その場合、 q[0]と q[1]が独立に、それぞれ50%の確率で0か1の値をとる。すなわち00, 01, 10, 11が(多少のばらつきがあるが)それぞれ25%の確率で現れる。これも古典ビットを用いた2ビットの乱数生成と同じ結果である。
実機による計算(ミス)
以上は、量子コンピュータのシミュレータを用いた理論的な計算結果であった。次に量子コンピュータの実機を用いてプログラムを実行する。プログラムの実行には、IBM Quantum Lab からアクセスできる量子コンピュータを用いる※7。
まず最初に、前述の「Hello, World!」ならぬ「Hello, Quantum!」プログラムを、2020年に開発された5量子ビットの「ibmq_quito」で実行してみる。IBMの量子コンピュータには、世界中のIBMの所在地にちなんだ名前が付けられていて、quito(キト)はエクアドルの首都の名前である。ただし、この地名は実際のコンピュータの所在地とは関係がない。なお、IBMは量子コンピュータの速度を表す指標としてCLOPS(1秒あたりに実行できる量子回路層の数)を提案している。その指標によると、このbmq_quitoの速度は2.5K CLOPSである。
このプログラムの4000回の実行には2.77秒を必要とした。一回あたりの実行に必要な時間は、約0.7msである(1秒間に約1444回プログラムを実行できた)。1946年に開発された世界最初期のコンピュータENIACが、10桁×10桁の乗算に約2.8ms必要とした(1秒間に約360回の乗算ができた)こと、そして1971年に発表・生産された、世界初の民生用1チップの4ビットマイクロプロセッサである「Intel 4004」(最大クロック周波数750KHz)が、符号なしの16桁の加減算の演算を実行に約1.6ms必要とした(1秒間に約625回の乗算ができた)ことを考えれば、この量子コンピュータが、すでにかなりの性能を持っていることがわかる※8。
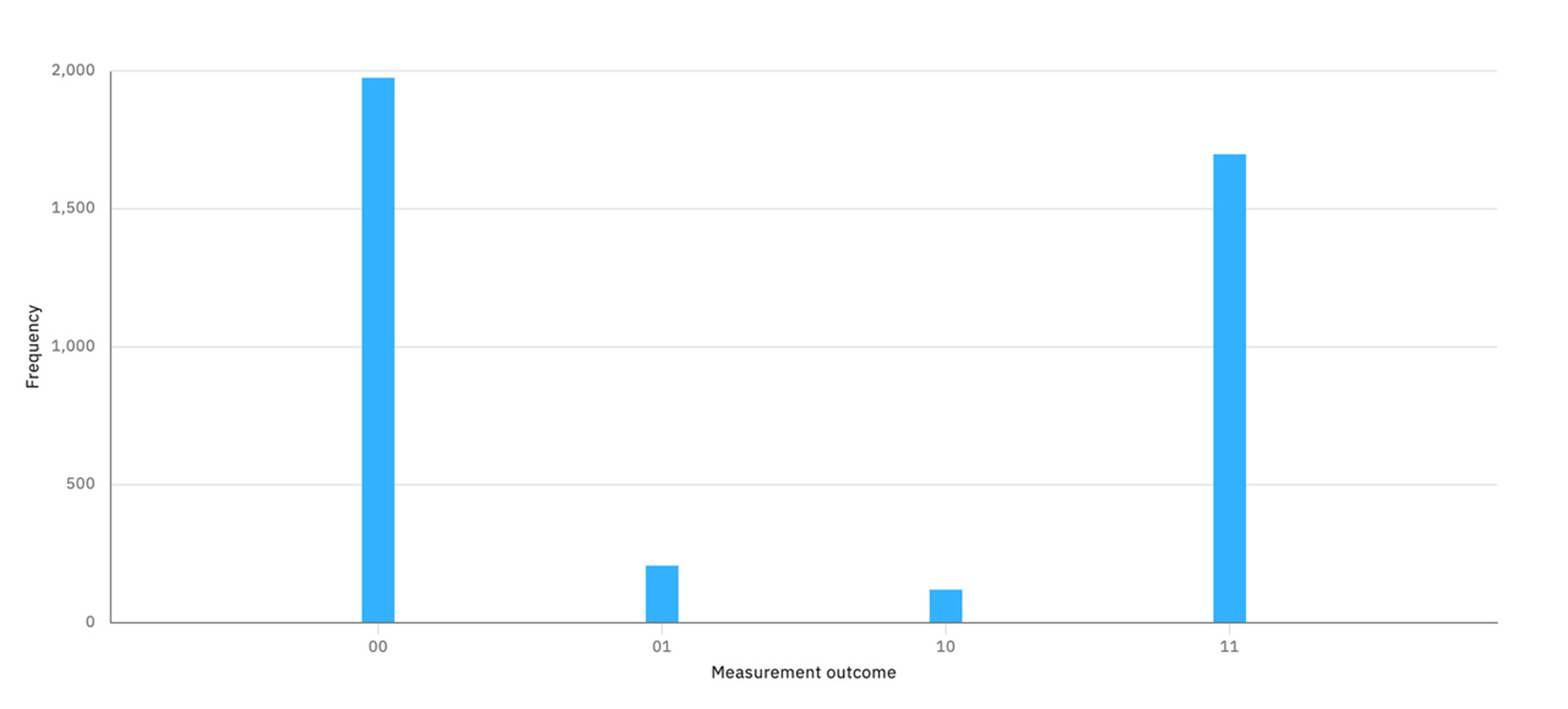
実機による計算結果(全4000回)を見ると、半々の確率で得られる00と11の割合が少し偏っていることに加えて、01と10という、理論的には得られない結果も測定されている。
- 00:1935回(48.4%)
- 01:116回(2.9%)
- 10:154回(3.8%)
- 11:1795回(44.9%)
これは、実機の計算エラーによるものである。量子状態は非常に壊れやすく、ノイズにとても弱い。現在の量子ビットや量子ゲートは、1000回に1回程度の確率でエラーを起こす。これは量子の不確定性(確率性)とは別の要因によるものである。このように、量子状態という物質の状態を基礎とする量子コンピュータにとって、実行時のエラーは不可避のものであり、このエラーを制御していかに小さくしていくかは、量子コンピュータのハードウェア開発における重要なテーマとなっている。
同じプログラムを、同様の性能を持つ別の実機である「ibmq_belem(ベレン:ブラジル北部のパラー州都)」で実行してみると、以下のような結果になった。
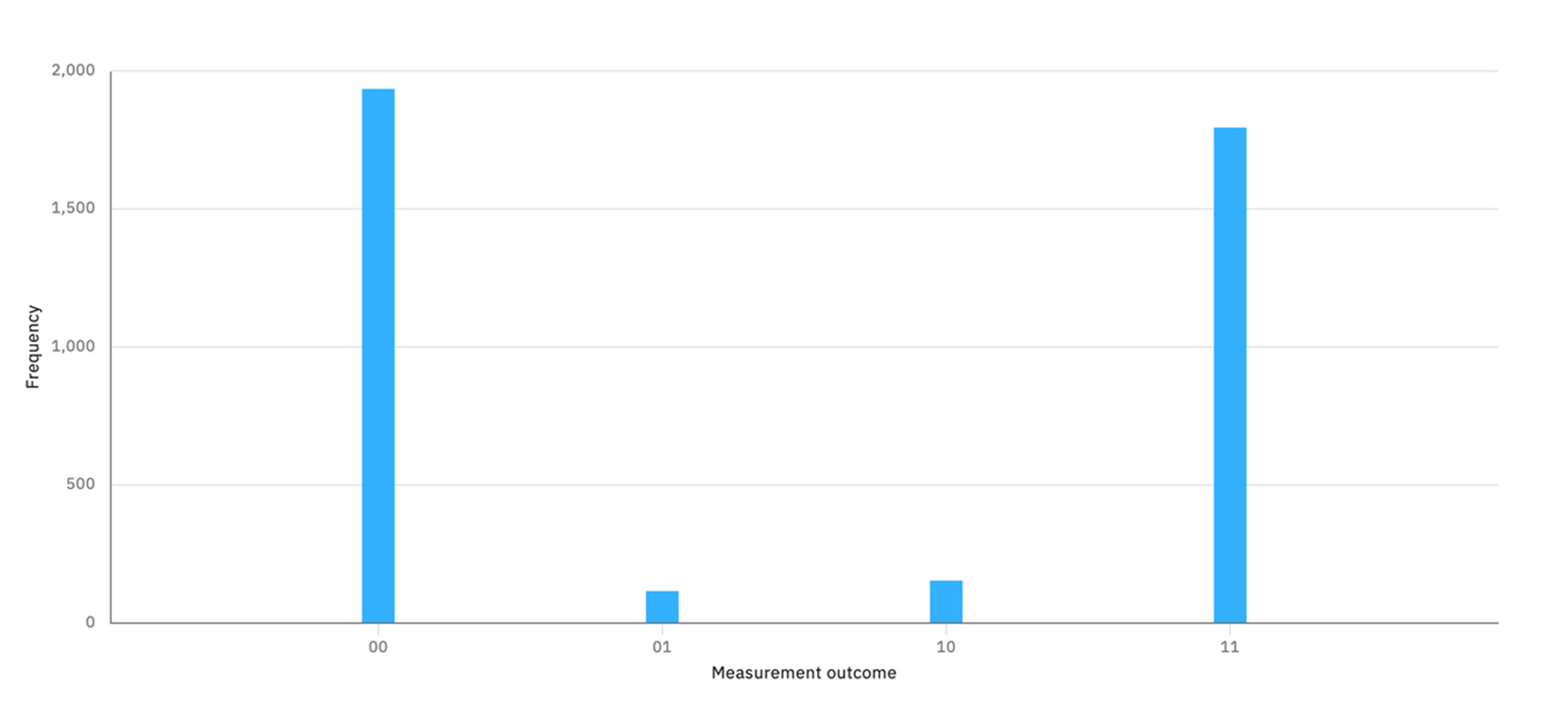
測定結果は
- 00:1975回(49.4%)
- 01:207回(5.2%)
- 10:120回(3.0%)
- 11:1698回(42.4%)
であり、やはり数%オーダーのエラーが発生している。今日の古典デジタルコンピュータにおいては、実行時のエラー、つまり計算ミスの対策が進んでいて、ほとんど考える必要がないのに対し、量子コンピュータの場合、この物理的な「計算ミス」が大きな影響を与える。正確さを第一とする量子コンピュータの理工学的な利用とは異なり、量子コンピュータアートにおいては、この計算ミスの意味や役割を、正確さとは別の観点から考える必要がある。
量子計算とはどのような計算か?
ここまで量子計算の理論と実際の簡単な例を見てきたが、これらを踏まえて量子計算とは、いったいどのような計算なのかを簡単にまとめておきたい。
まず初めに、量子計算は量子ビットという「物質」を用いた計算である。ゲート型の量子コンピュータは、量子ビットの物理的な状態を量子ゲートによって変化させることで計算を進めていく。量子計算は電子回路を用いた計算のように、量子ビットの連続的(アナログ)な状態を用いて計算を実行する。こうしたアナログ計算は、今日広く自然計算と呼ばれている※9。
しかしながら最初に述べたように、複数の状態を同時に持つ量子ビットの重ね合わせ状態は、何かひとつの定まった値を持たず、ひとつの値を得るためには、量子ビットを測定するしかない。同じ量子状態においても、その結果は測定毎にばらつき、測定値の確率的、統計的な分布しか得られない。しかも、測定によって知り得る情報は、量子ビットの状態そのものではなく、古典ビット同様の0と1のバイナリデータである。最終的な計算結果は、測定による古典デジタル値としてしか得られない。量子状態はアナログ値で、測定することでデジタル値となる。量子計算は、自然計算であると同時に、測定というインターフェイスによって、アナログとデジタルを結びつける、ハイブリッド計算のひとつである。
最終的な測定結果がデジタルであったとしても、アナログな量子状態はノイズに弱く、常に少なからぬ誤差やエラーが存在する。量子状態がアナログであるがゆえに、測定結果には必ずエラー(計算ミス)が発生する。これも、計算ミスが(ほとんど)問題にはならない古典コンピュータとの大きな違いである。量子コンピュータには、量子状態そのものが持つ本質的な不確定性と、実機が持つエラーという現実的な不確実性の両者が存在する。
もつれ合いによって構造を与える
4量子ビットの系(4量子ビットコンピュータ)を考える。4つの量子ビットをアダマールゲートですべて重ね合わせの状態にしてから測定すると、0000から1111までの16通りの状態がすべて(ほぼ)均等に現れる。これは、古典コンピュータによる4ビットの一様乱数と同じ計算結果である。
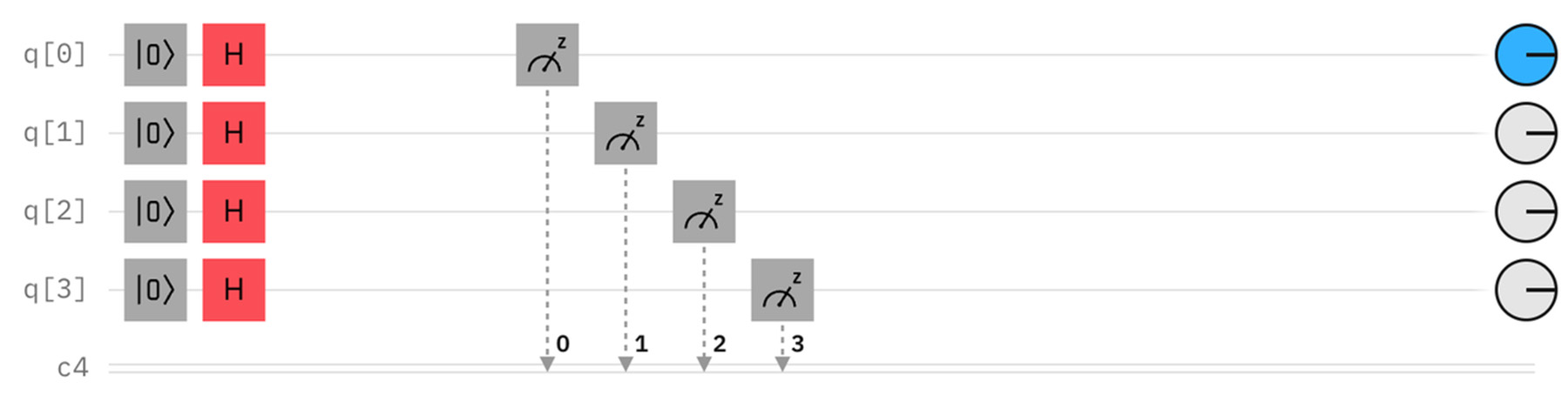
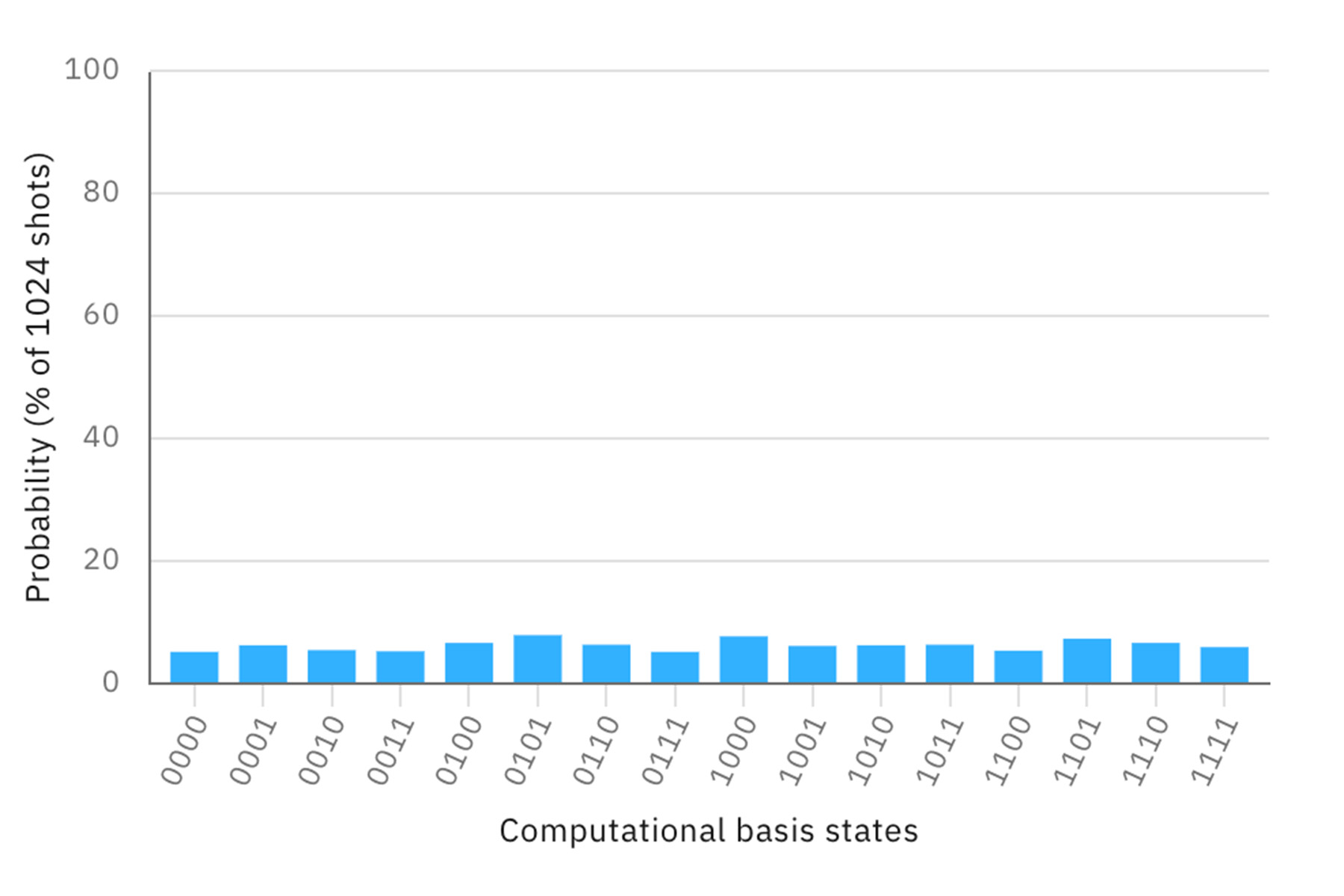
ここにもつれ合いによって、量子ビット同士に関係を与えると、測定結果に構造=パターンが出現する。例えば、最初の2つの量子ビットをエンタングルさせると、以下のような測定パターンとなる。
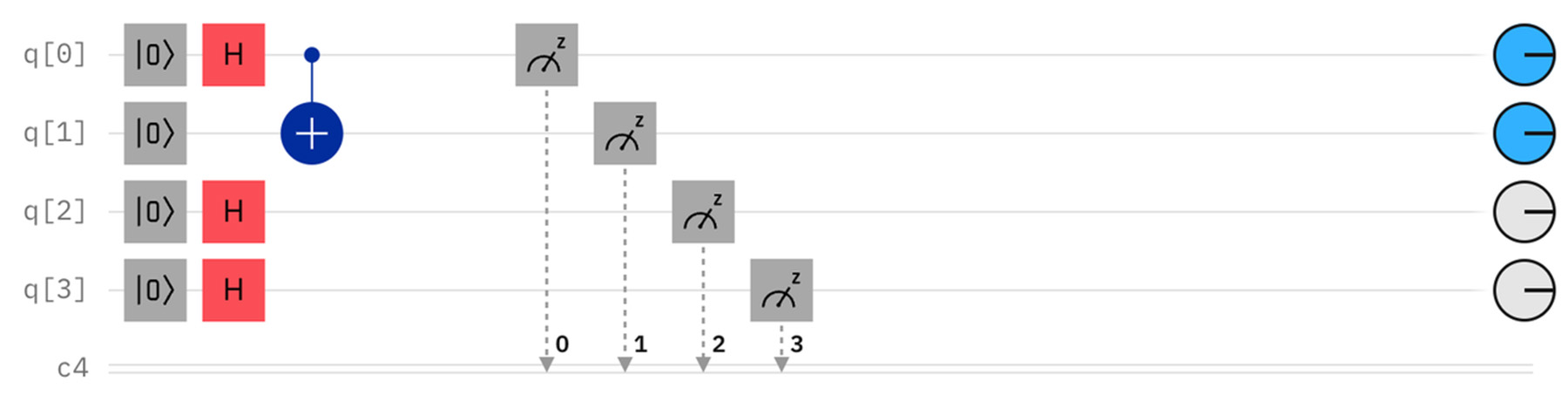
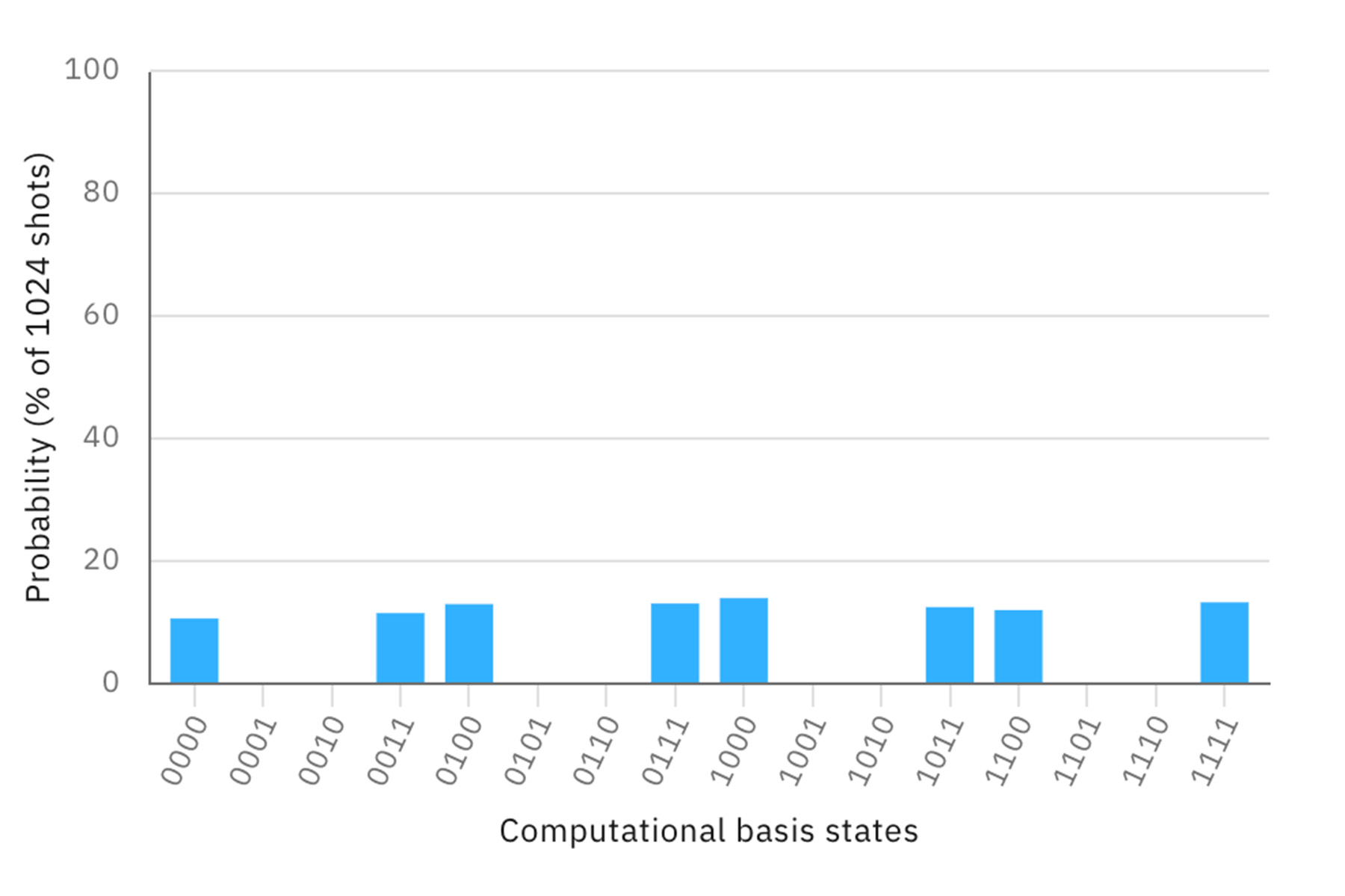
その他の2つの量子ビットをエンタングルさせると、別のパターンが出現する。
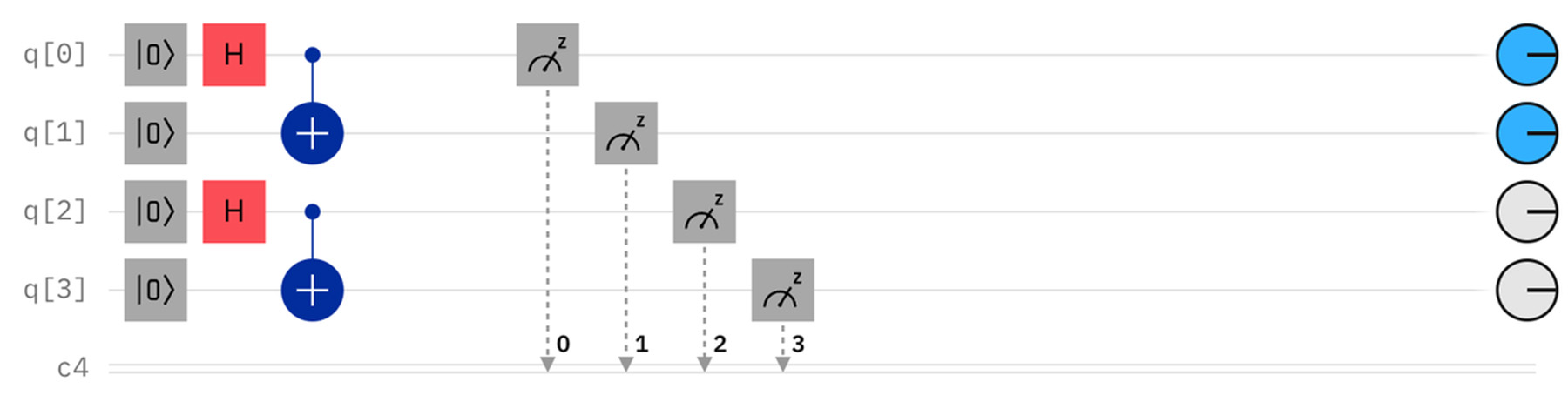
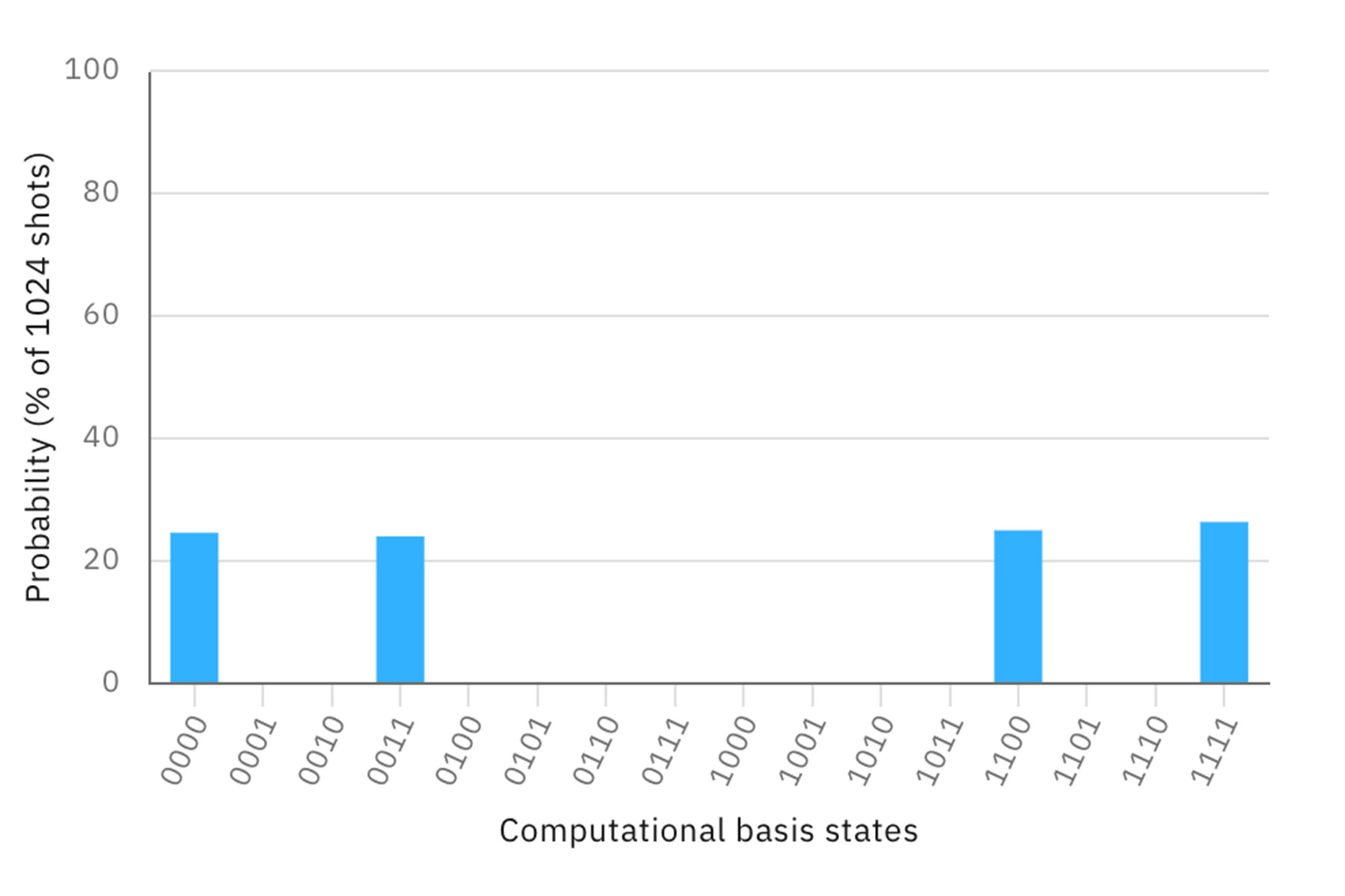
3つの量子ビットをエンタングルする(GHZ状態)と以下のようなパターンが生まれる。
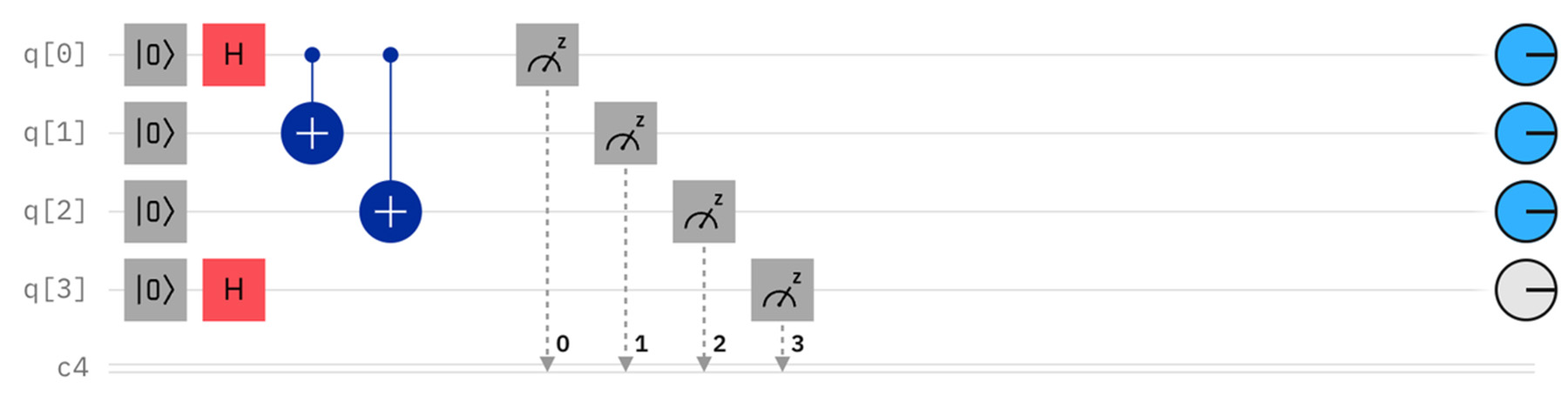
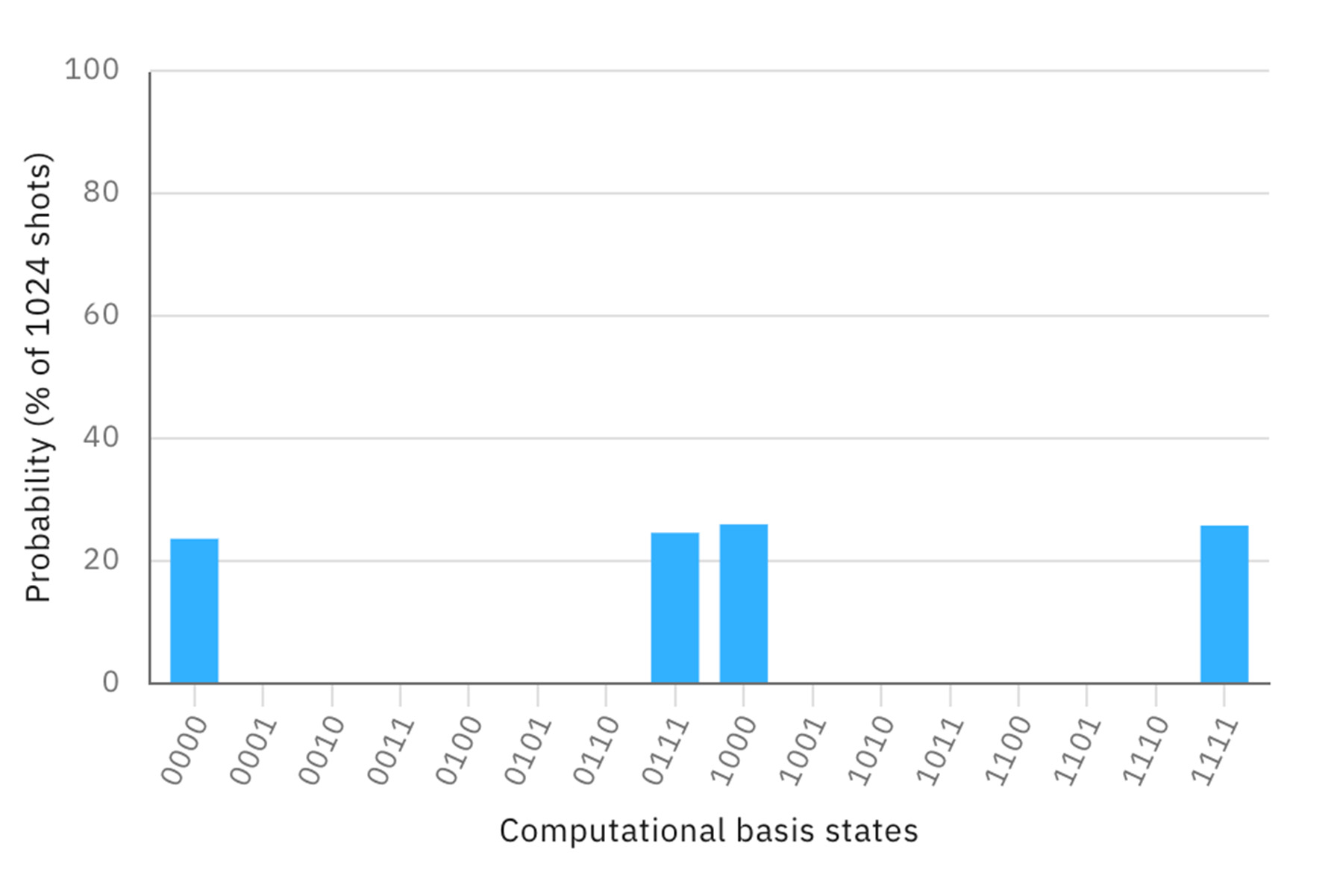
4つの量子ビットをすべてエンタングルさせると、0000と1111のいずれかしか出現しなくなる。
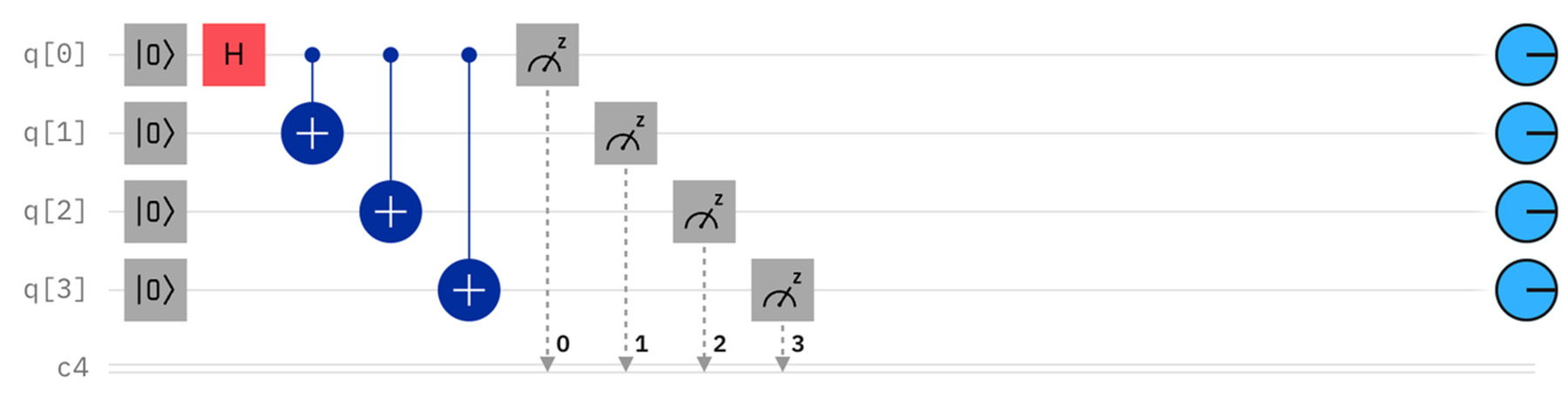
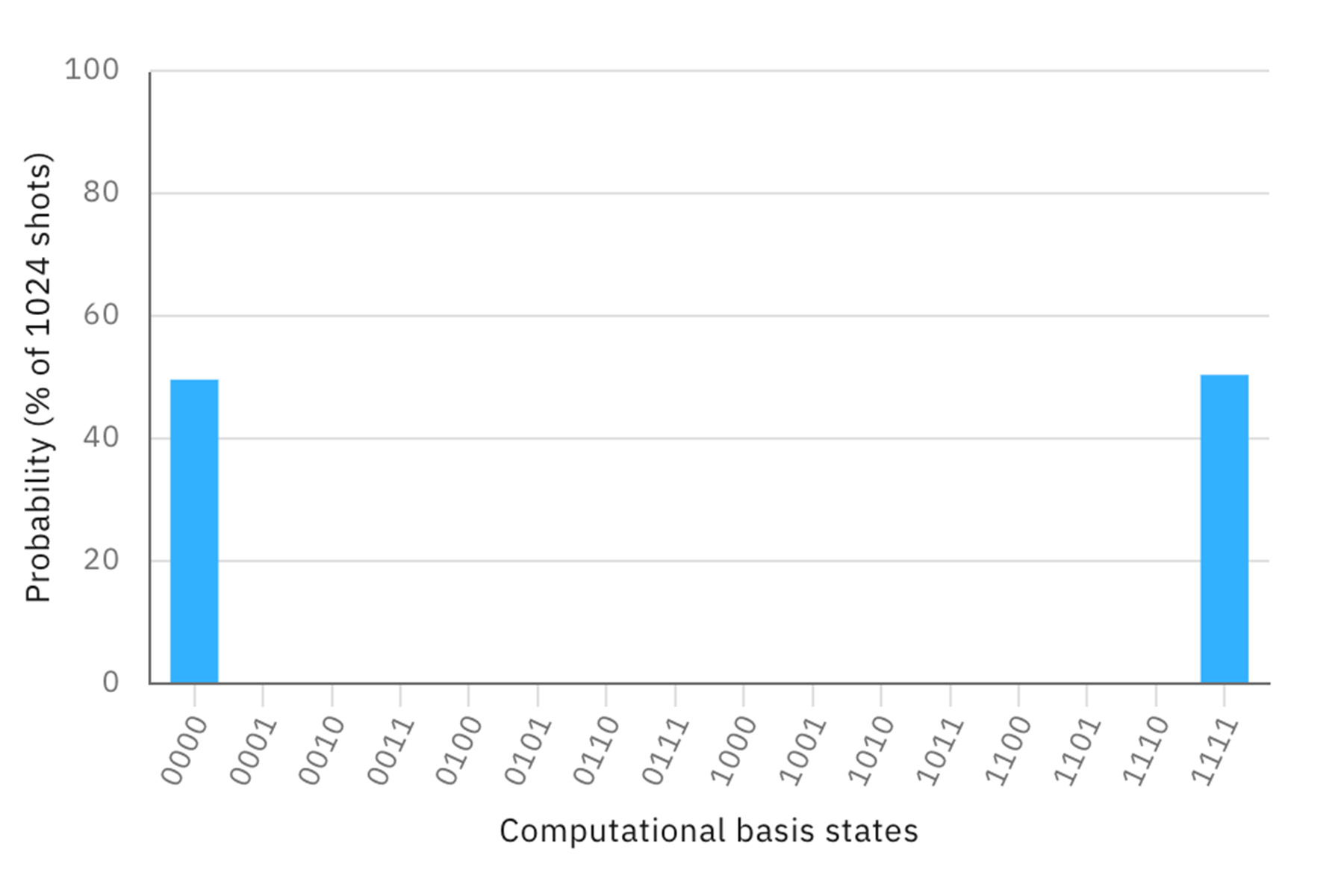
エンタングルさせる関係を変えても、結果は同じになる。
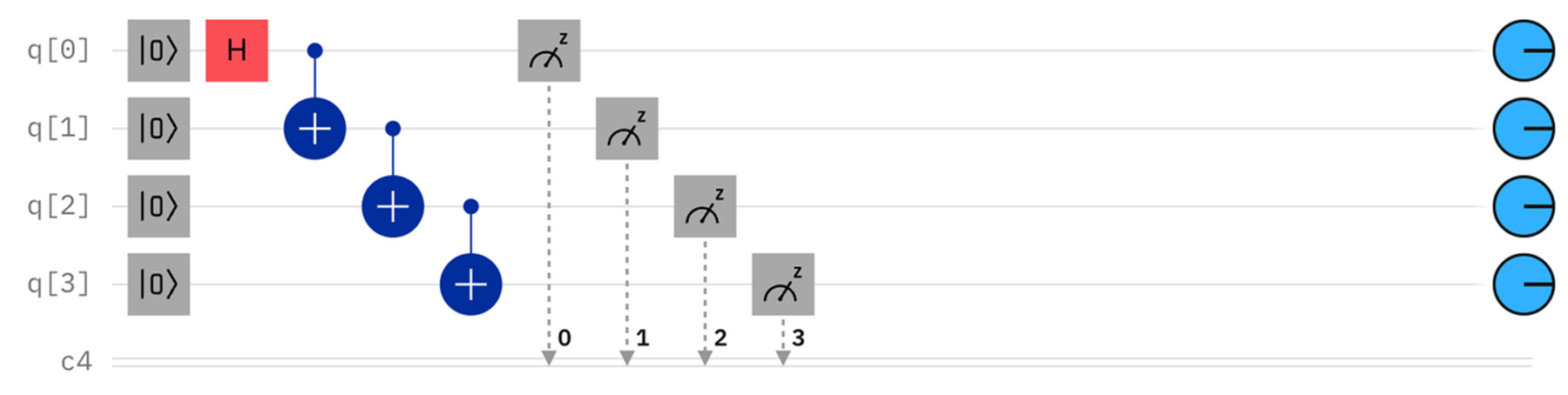
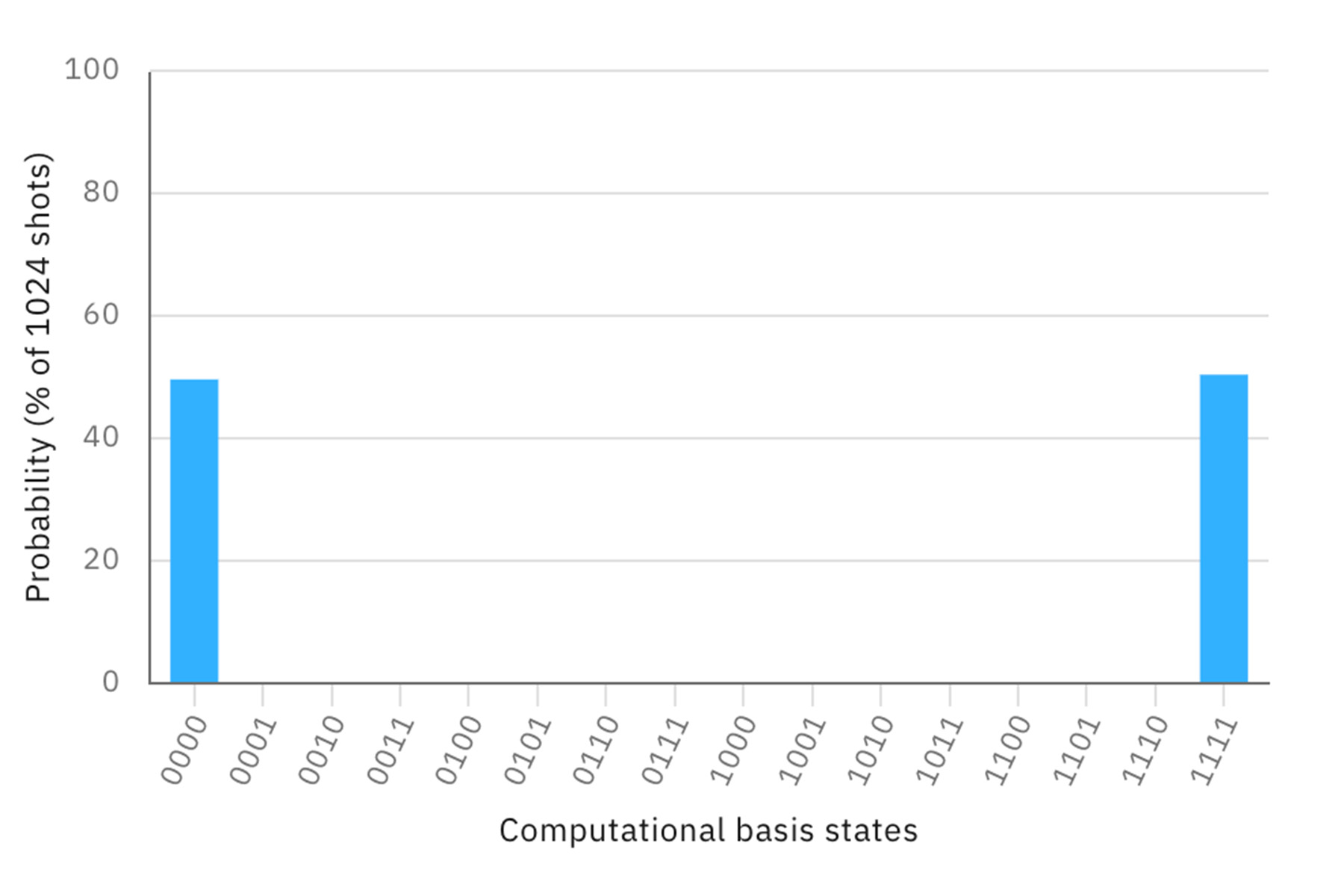
さらに、エンタングルした4つの量子ビットそれぞれに、再びアダマールゲートを適用してから測定すると、以下のような面白い結果になる。
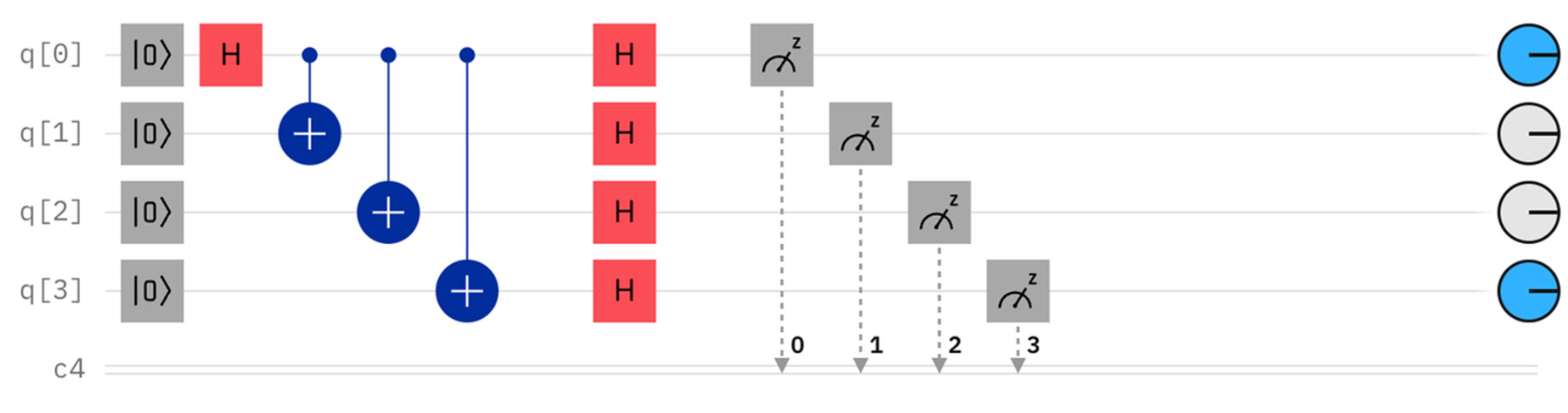
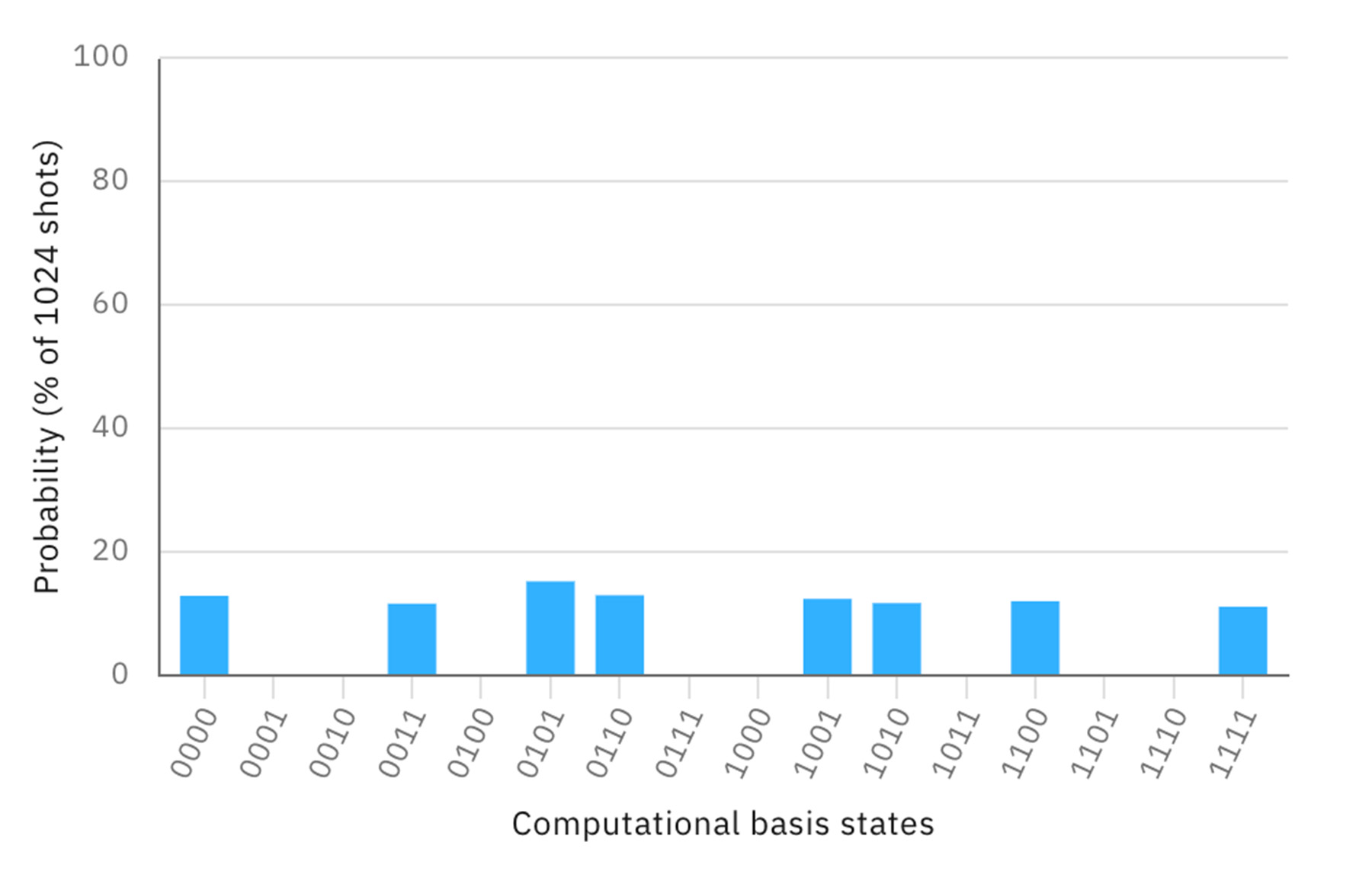
測定される結果は、1あるいは0の数が偶数(0, 2, 4)個のものだけとなり、すべての結果が等しく現れるもつれ合いなしの状況とは、大きく異なっている。
このプログラムを実機の「ibmq_manila(マニラ:フィリピン共和国の首都)」で4000回実行した結果が以下のとおりである。全体で17%程度のエラーが発生しているが、1あるいは0の数が偶数個の結果が多数を占めている。
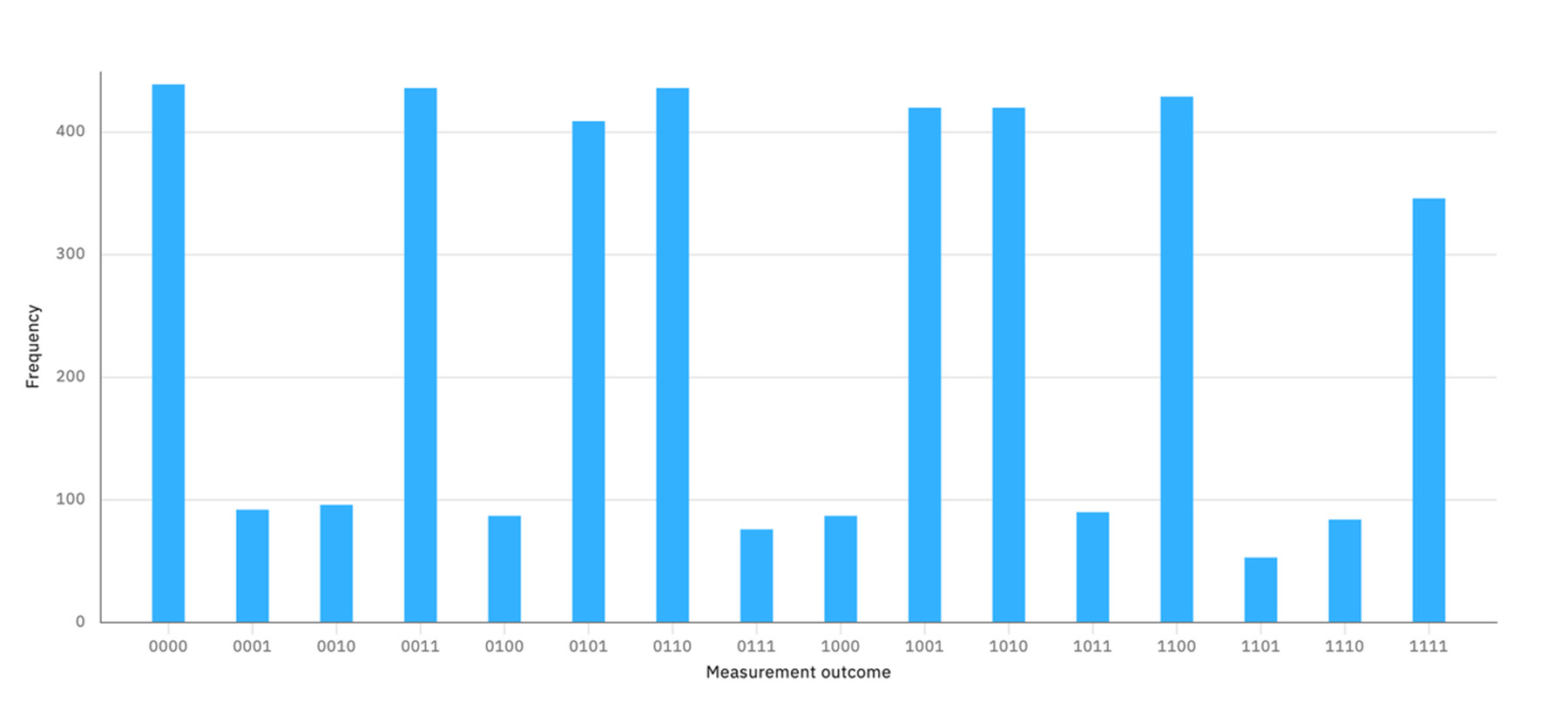
以上のように、量子プログラミングは、量子特有の重ね合わせの状態に、もつれ合いによってトポロジカルな構造を与えることで、測定結果の確率パターンを生成していくことと考えることができる。重要なのはもつれ合いと測定の構成にある。この、もつれ合いという関係によって重ね合わせ状態とその測定結果に構造を与えていく方法を、量子コンピュータによる「もうひとつの構成主義」と位置付けることもできるだろう。
作品の存在論:実行と鑑賞のもつれ合い
量子コンピュータによる芸術制作を考えるときに、次に検討しなければならないのは、その量子論的な実在と芸術活動の関係、すなわち量子コンピュータアート作品の存在論である。量子コンピュータが内蔵する量子ビット=作品の状態は、人間が直接知覚することができない、不可知の存在である。量子ビットを測定することによって、それは初めて人間にとって可知のものとなると同時に、量子ビット=作品の状態に影響を与える。
芸術活動において、この測定は鑑賞行為と関係がある。量子計算における測定行為を量子コンピュータアート作品の鑑賞行為と仮説的に対応させれば、作品制作とは、この測定=鑑賞にどのような確率分布を与えるか、すなわち多数の測定=鑑賞の統計分布をコントロールすることとなる。通常の鑑賞行為においては、その変動は鑑賞者と作品の関係によって決まるが、量子コンピュータアートの場合は、作品の存在そのものが量子の不確定性と、計算の不確実性を持つ。しかしながら、デジタルデータとして示される測定結果だけを問題にするのであれば、それは古典コンピュータでもシミュレート可能なものとなり、古典コンピュータアートと同等のものになってしまう。
そう考えたときに問題としなければならないのが「その測定=鑑賞行為をいつ誰が行うのか」ということになる。前述の事例では、各量子ビットに量子ゲートを適用した後、順次測定を行ったが、一部の量子ビットを測定して、残りの量子ビットをさらに量子ゲートで操作することも可能である。計算の実行プロセスと測定=鑑賞プロセスは明確に分けられるものではなく、両者の境界は曖昧であり、不可分である。なぜなら、測定=鑑賞は、計算する対象=作品に影響を与え、最終的な測定結果にも影響を与えるからである。カメラを向けると人の行動が変化したり、物音を立てると動物が逃げたり、日常生活の中でも観測が対象に影響を与えるのは当たり前のことであるが、量子コンピュータアートの場合、それが作品の存在そのものに対して、本質的な影響を与える。
例えば、先ほどの4つの量子ビットをすべてエンタングルさせたプログラムにおいて、4つ目の量子ビットに制御CNOTゲートを適用する前に、すなわち q[3] (一番左側の桁)がもつれ合う前に測定すると、以下のように最終結果が変化する。
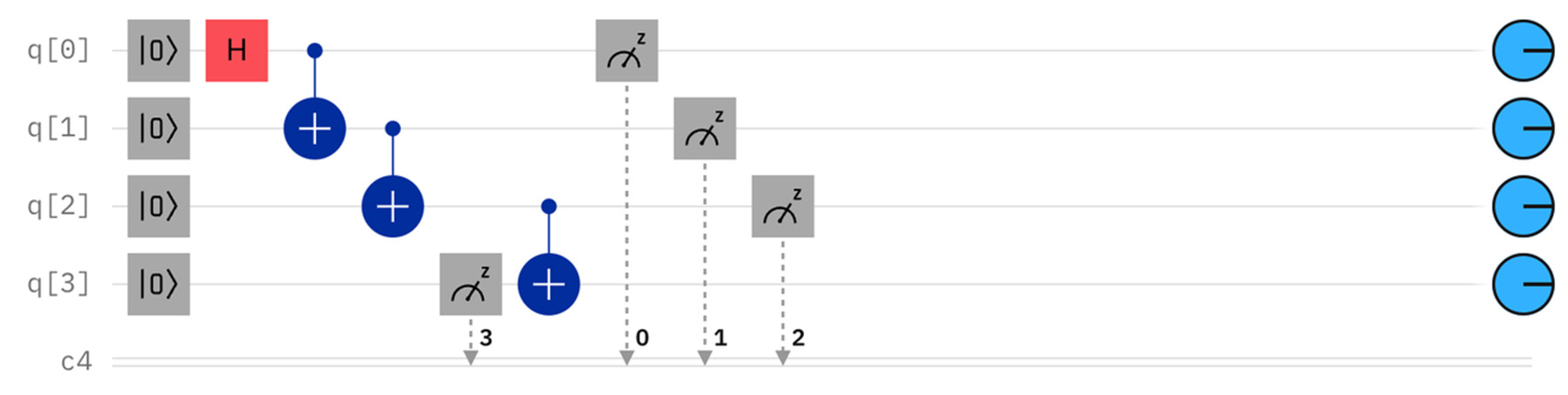
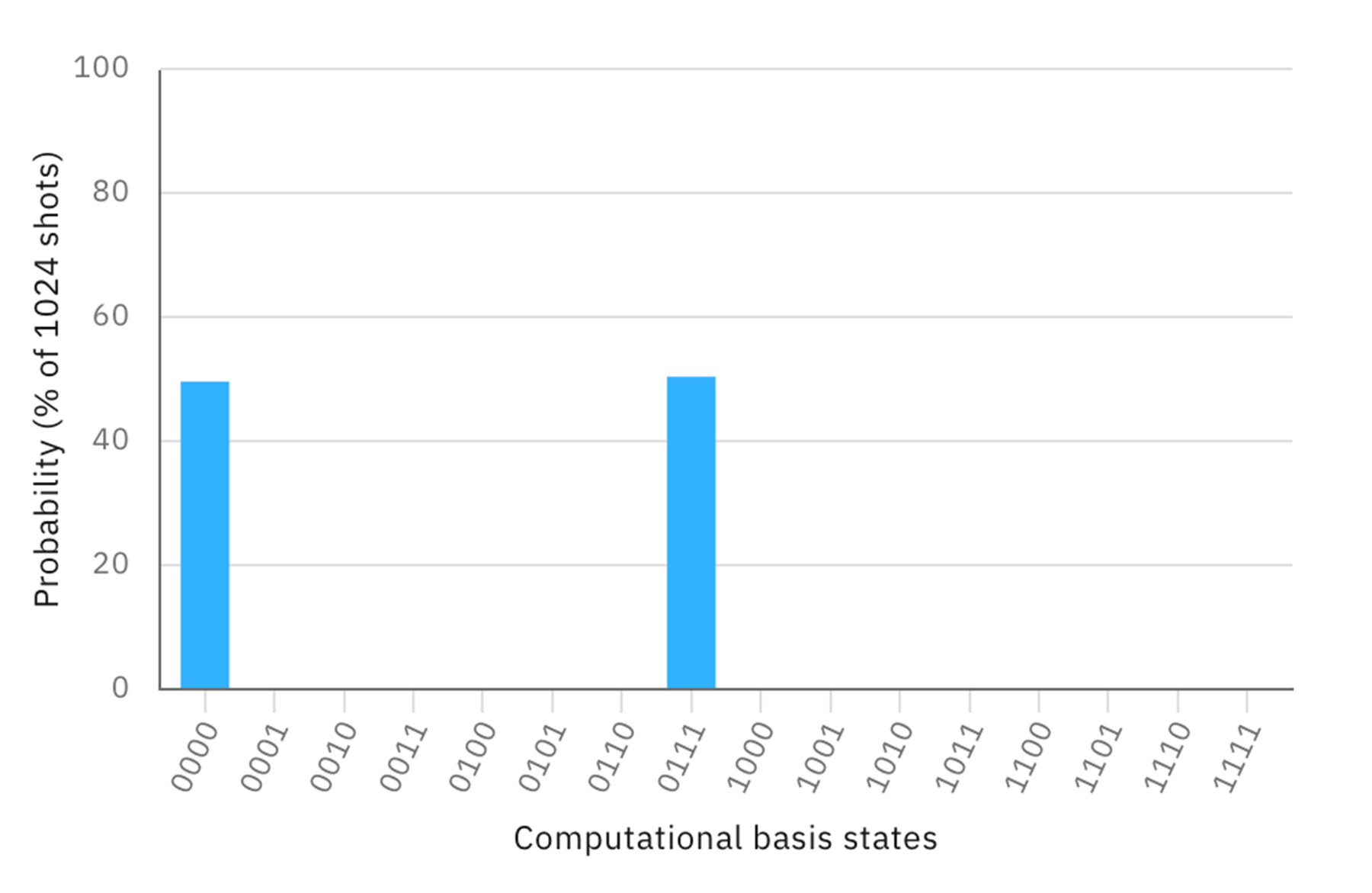
今回紹介したのはゲート型と呼ばれる、最も一般的な量子計算だったが、最初にまずエンタングルした量子状態を準備しておき、量子ビットをひとつずつ測定していくことで計算を進めていく「測定型量子計算」という計算方法もある※10。このように、量子コンピュータアートにおける測定=鑑賞行為については、さまざまな観点から議論を深めていく必要がある。計算の実行と観測が相互に影響を与えるという意味では、鑑賞は内在的な行為であり、量子状態にある作品そのものが、鑑賞者の存在抜きには存在しない。完成して変化することのない対象に対して、さまざまな視点や方法で体験したりや批評を行う古典的鑑賞に対して、量子コンピュータアートの鑑賞行為とは、作品と鑑賞者のインタラクションのプロセス自体を実践、記録、考察し、そこから何が生まれるのかを見極めていく「生成型鑑賞」といえるだろう。
「量子テレポーテーション」という、もつれ合った2つの量子ビット q[1] と q[2] を利用して、量子ビット q[0] の状態を q[2] に転送するプログラムを考える。 q[0] と q[1] の2つの量子ビットを測定によって古典ビット化してから、その値に応じて( q[1] と離れた場所にあってもいい) q[2] に適切な量子ゲート処理を行うと、 q[2] の量子状態が測定前の q[0] と同じものになる。これは作品の一部を鑑賞(測定)することによって、新たな作品(量子状態)を別の場所に生成する、計算と測定が密接に関わり合うアルゴリズムの一例である。
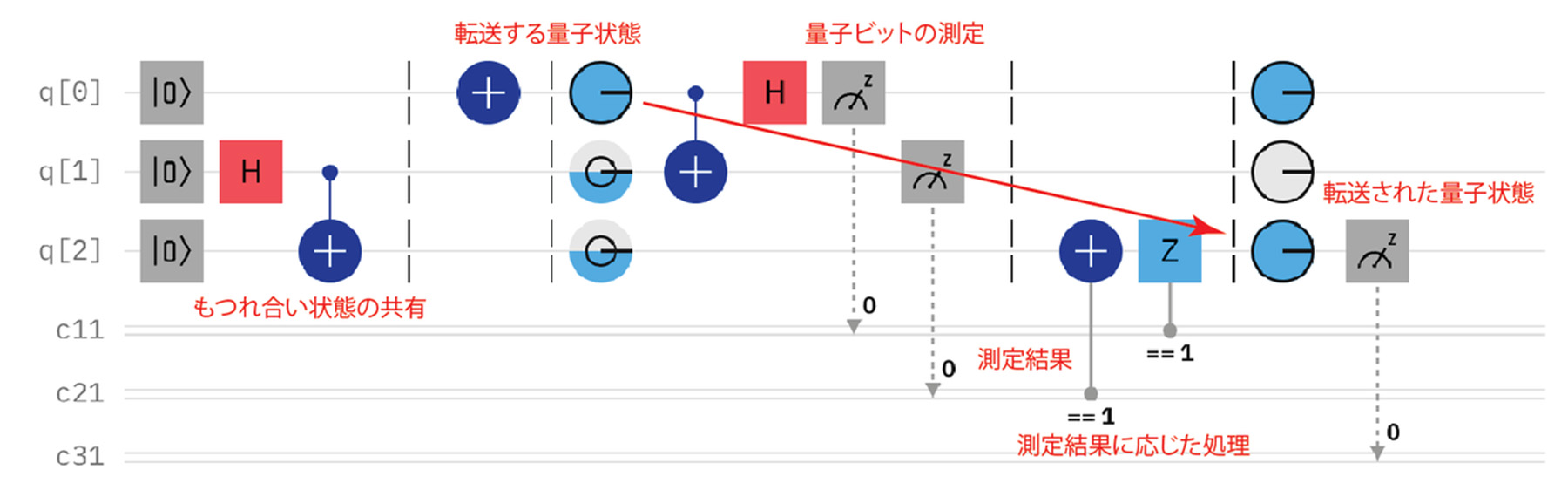
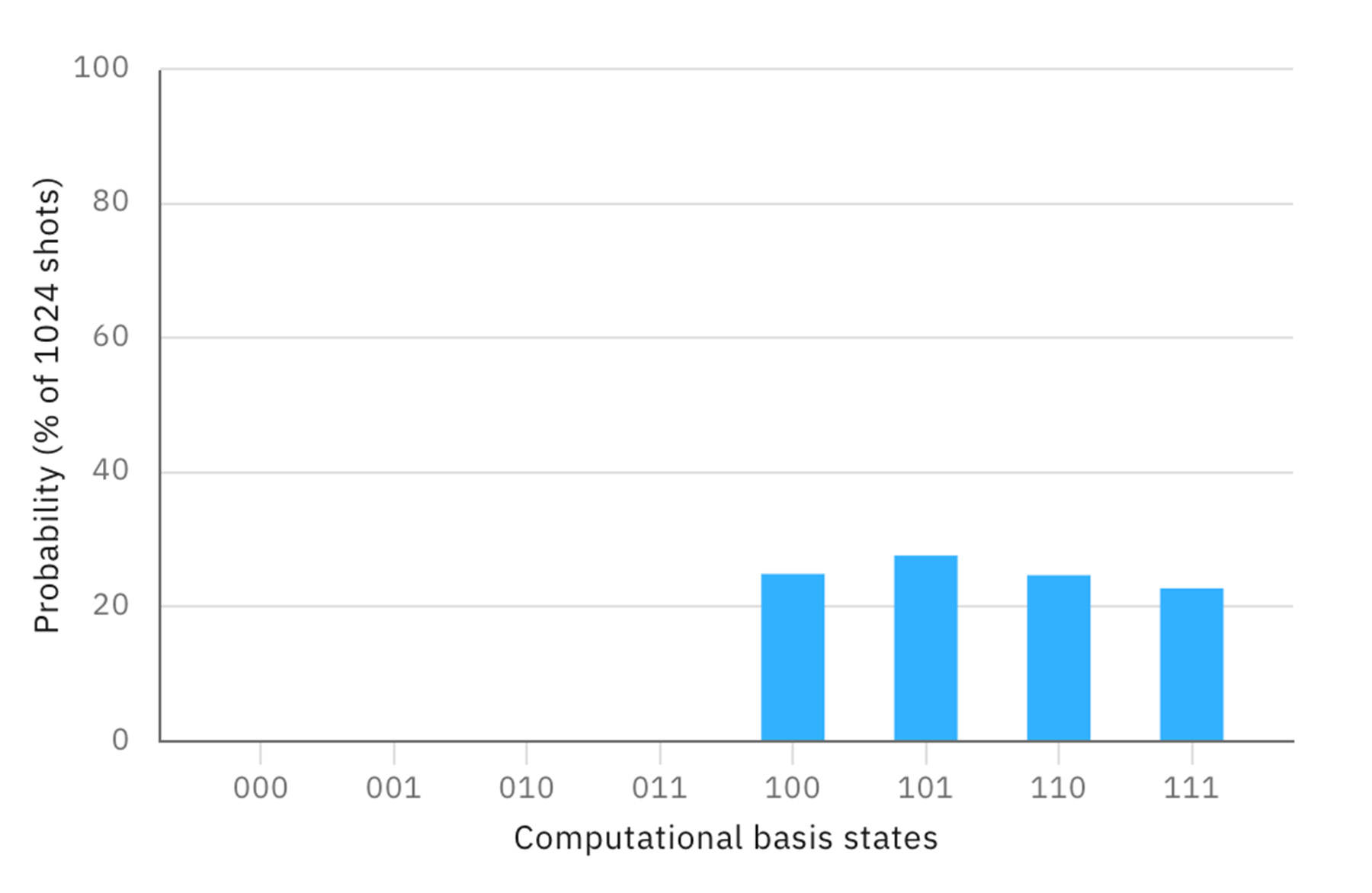
最も左側の桁が q[0] を転送した q[2] の測定結果である。NOTゲートによって |1⟩ となった量子状態を転送したので、最も左側の桁の値はすべて1となっている。
エンタングルメント・セレンディピティ
こうした、量子コンピュータアートにおける計算の実行と測定、すなわち作品(量子コンピュータ)と鑑賞(測定者)、さらには測定装置に相当する「鑑賞の場」の不可分性について考えていくと、それを相互作用に先立つ独立した個体要素を前提とするインタラクションではなく、むしろカレン・バラッドが提示した「イントラ−アクション(intra-action)」、すなわち測定結果という個体要素が生まれる以前の相互関係と捉える方が適していることがわかる※11。
バラッド自身は、この「イントラ−アクション」という概念を、もつれあうエージェンシーたちの相互的構成と捉え、この概念を表象主義を乗り越えるための、ものとひとがもつれ合ったポスト人間主義的なフェミニズム理論へと繋げていった。その一方でこの概念をHCI(Human-Computer Interaction)の基本的な前提に対する、批判的問い直しに適用しようとする動きもある※12。
バラッドの発想の源となったのは、物理学者ニールス・ボーアの量子論であり、量子コンピュータが、バラッドが強調する「物質の能動的な役割」を中心に置いた装置であるのは、いわばあたりまえのことかもしれない。だから、すでに存在している実体に主体性を帰さない「エージェンシャル・リアリズム」の概念は、量子コンピュータアートの中核を成している。量子状態の系(量子ビット群)に「もつれ合い」という関係を設定することで生まれるこのエージェンシーこそが、測定という「エージェンシャル・カット」をもたらし、この切断によって量子コンピュータに内在する存在論的な不確定性が解消される。インタラクティブアートにおける「わたしたちはわたしたちが鑑賞しようとする作品の一部である」という考え方を、作品の存在や鑑賞という行為そのものにまで拡張するのが、イントラ−アクティブな量子コンピュータアートであるといえる。
学芸員のヤシャ・ライハートは1968年に、ロンドンのICA(Institute of Contemporary Arts)で「サイバネティック・セレンディピティ」と名付けられた展覧会を企画・開催した※13。数学者ノーバート・ウィーナーのサイバネティクスと「偶然に出会ったり、予想外のものや別の価値があるものを発見すること」という意味を持つセレンディピティという語を組み合わせたこの展覧会名と同等の期待を、今日の量子力学や量子コンピュータに対しても掲げてみたい。サイバネティクスの概念が、その後の古典コンピュータアートやインタラクティブアートにつながっていったように、量子のもつれ合い状態―エンタングルメントは、芸術の存在論、創作行為と鑑賞行為に対して、人間スケールの素朴実在論では得られない非直感的な視点を投げかける。それはさらに、世界の動的かつトポロジカルな再構成や再分節をもたらす、未来のイントラアクティブアートへとつながっていく可能性がある。
量子コンピュータアートとはどのような芸術か?
量子コンピュータがもたらしたものは、素朴実在論の常識を超える、エンタングルメントによる人間の認識の飛躍である。さらに量子の複製不可能性は、コンピュータアートや量子情報に本質的な唯一性を与え、非常に壊れやすい量子状態は、計算エラーを生み出すだけでなく、保存、再現不可能な一回性を生み出す。加えて、作品の不確定性=測定の確率的ばらつきは、一回、あるいは少数の計算結果を作品〜鑑賞対象としてきた古典コンピュータアートから、多数の測定結果の統計値を得るプロセス自体を鑑賞行為とすることへのトランジションと、その意味の問いかけをもたらす。
こうした量子コンピュータアートの特徴を踏まえて、冒頭の川野洋のステートメントを量子コンピュータアートのためにリライトすることで、本稿を締めくくりたい。
量子コンピュータアートとは何か?それは量子ビットという量子状態にある物質を素材とする芸術である。芸術活動の主体は量子コンピュータとそれを測定する人間が深く結びついたハイブリッドな系である。……我々の目指す量子コンピュータアートとは量子状態という人間には不可知の実在を芸術創造の素材とする量子コンピュータのアートであり、局所的な古典コンピュータによる芸術とも、素朴実在論に根差した人間芸術ともその理念を異にするものである。
量子コンピュータは量子ビットという量子状態の物質を内蔵し、その物質を操作することで自動的に情報を処理(計算)をする、言うなれば自然を模した機械であり、その一切の動作はプログラムによって実行される。しかしながら、量子コンピュータがこのプログラムに従って自発的自律的に動作するだけでは不十分である。重ね合わせやもつれ合いの状態にある量子ビットを計測装置+人間系が何回も測定することで、初めて人間が知覚可能な作品が統計的に現出する。このようなコンピュータと人間を含む、実在レベルでのイントラ−アクションの芸術を我々は真正量子コンピュータアート(量子コンピュータの芸術)と呼ぶ。

