Uncreative Quantum Coding / アンクリエイティブ・量子コーディング

ChatGPTと一緒に量子コーディングする

量子コンピュータアート^※1の習作として、Open AIのChatGPT^※2（GPT−4）を用いた、Uncreative Coding^※3を行ってみる。

まず初めに、ChatGPTに以下のようなコードの生成を依頼する（実際のChatGPTとの対話は英語で行った）。

すると以下の前置きと共にQiskitのコードが提示された。

from qiskit import QuantumCircuit, Aer, transpile
from qiskit.visualization import plot_histogram
from qiskit.providers.aer import AerSimulator

# Define the number of qubits
n_qubits = 10  # You can change this number

# Create a quantum circuit
ghz_circuit = QuantumCircuit(n_qubits)

# Create a GHZ state
ghz_circuit.h(0)  # Create a superposition on the first qubit
for qubit in range(1, n_qubits):
ghz_circuit.cx(qubit-1, qubit)  # Create entanglement with the previous qubit

# Measure the qubits
ghz_circuit.measure_all()

# Visualize the circuit
ghz_circuit.draw('mpl')

# Simulate the circuit
simulator = AerSimulator()
compiled_circuit = transpile(ghz_circuit, simulator)
result = simulator.run(compiled_circuit).result()

# Get and display the histogram of results
counts = result.get_counts()
plot_histogram(counts)

1. まずQiskitから必要なライブラリをインポートします。
2. 次に、もつれ合わせたい量子ビットの数を定義します。
3. 指定された数の量子ビットで新しい量子回路を作ります。
4. 最初の量子ビットにアダマールゲート(h)を適用し、重ね合わせ状態を作ります。
5. 次に、ループを使って一連のCNOTゲート(cx)を適用し、後続の各量子ビットを前の量子ビットにもつれさせ、GHZ状態を作ります。
6. すべての量子ビットを測定し、回路を可視化します。
7. 最後に、QiskitのAerSimulatorを使って回路をシミュレーションし、結果のヒストグラムを表示します。

このコード IBMのQuantum Lab^※4で表示、実行する。まず、コードを図で表現すると、以下のような10個の量子ビットが一様にもつれ合わせるものであることがわかる。

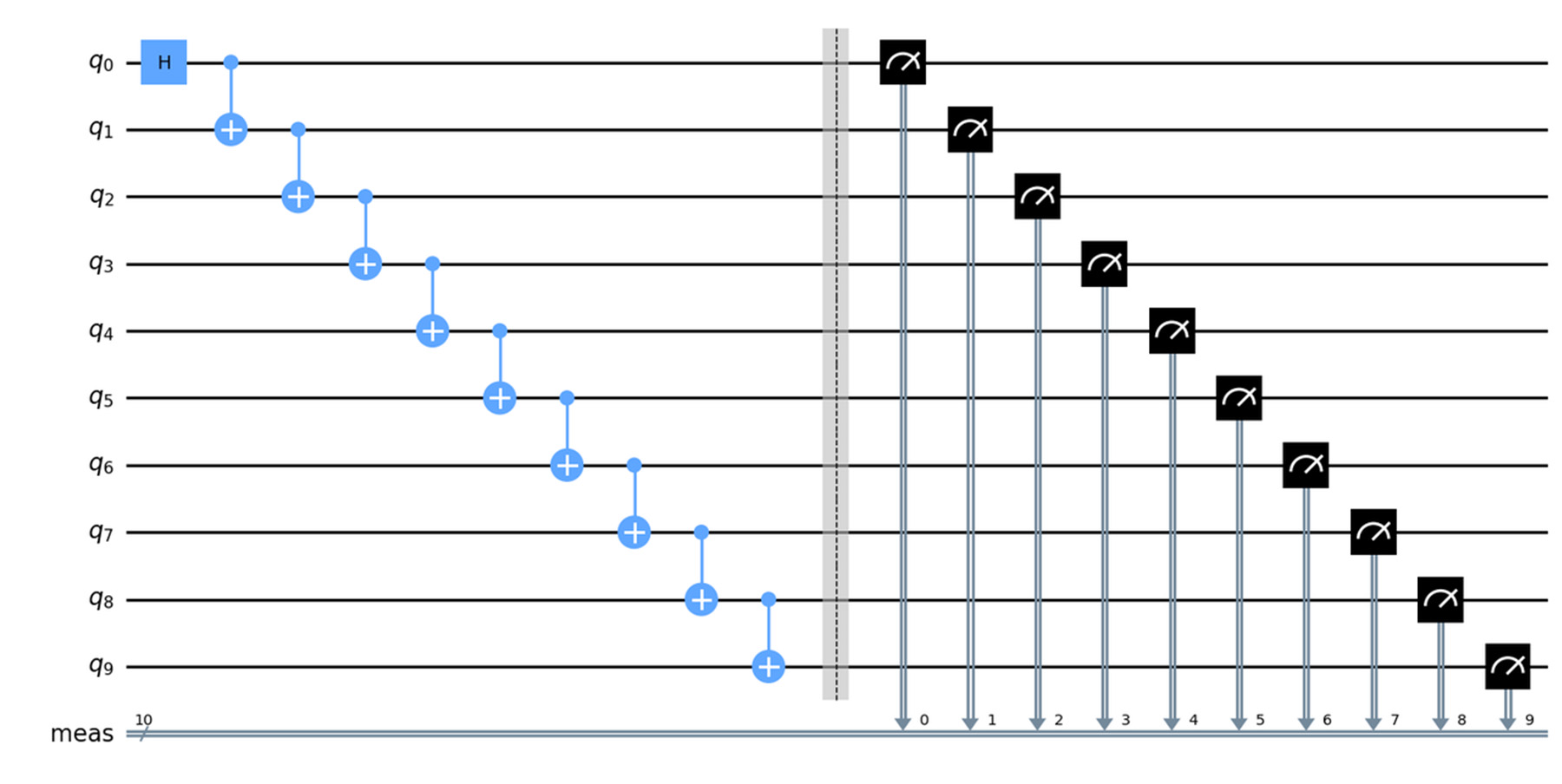
このコードをシミュレータで1024回実行すると、以下のヒストグラムが得られる。量子ビットが一様にもつれ合っているため、その測定結果はすべて0（00000000）あるいは、すべて1（11111111）のいずれかとなり、両者がほぼ均等に現れる。

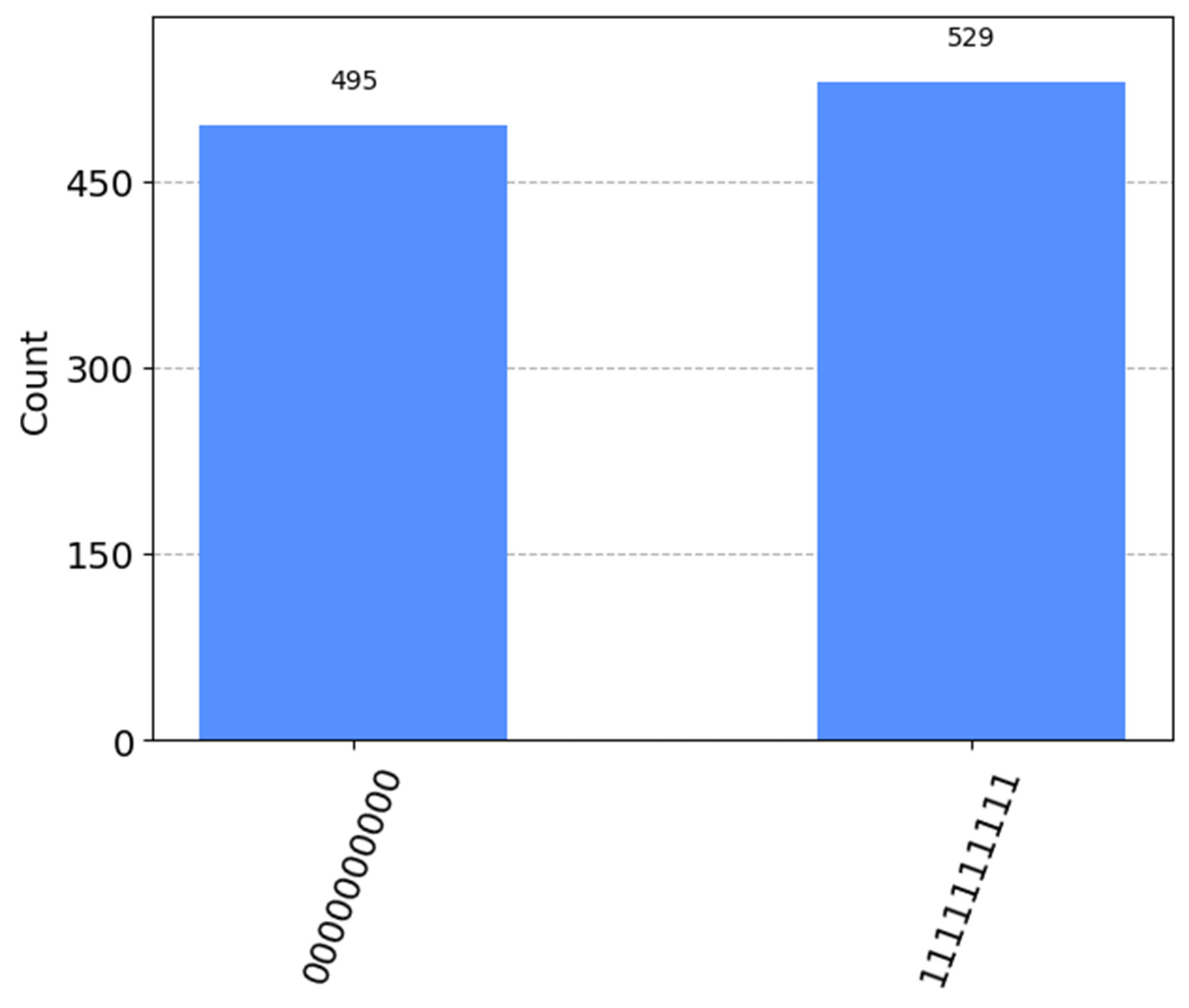
もつれ合いによる構造の生成

次に、ChatGPT-4に以下のような依頼を行った。

すると以下のようなコードが提示された。

from qiskit import QuantumCircuit, Aer, transpile
from qiskit.visualization import plot_histogram
from qiskit.providers.aer import AerSimulator

# Define the number of qubits
n_qubits = 10  # You can change this number

# Create a quantum circuit
circuit = QuantumCircuit(n_qubits)

# Create a more complex entanglement structure
circuit.h(0)  # Create a superposition on the first qubit
circuit.cx(0, 1)  # Entangle qubits 0 and 1
circuit.cx(1, 2)  # Entangle qubits 1 and 2
circuit.h(3)  # Create a superposition on the fourth qubit
circuit.cx(3, 4)  # Entangle qubits 3 and 4
circuit.cx(4, 5)  # Entangle qubits 4 and 5
circuit.cx(2, 6)  # Entangle qubits 2 and 6
circuit.cx(6, 7)  # Entangle qubits 6 and 7
circuit.h(8)  # Create a superposition on the ninth qubit
circuit.cx(8, 9)  # Entangle qubits 8 and 9

# Measure the qubits
circuit.measure_all()

# Visualize the circuit
circuit.draw('mpl')

# Simulate the circuit
simulator = AerSimulator()
compiled_circuit = transpile(circuit, simulator)
result = simulator.run(compiled_circuit).result()

# Get and display the histogram of results
counts = result.get_counts()
plot_histogram(counts)

1. まずQiskitから必要なライブラリをインポートする。
2. 次に、もつれ合わせたい量子ビットの数を定義する。
3. 指定された数の量子ビットで新しい量子回路を作成する。
4. 一連のアダマールゲートとCNOTゲートを適用し、量子ビット間でより複雑なエンタングルメント構造を作ります。
5. すべての量子ビットを測定し、回路を可視化する。
6. 最後に、QiskitのAerSimulatorを使って回路をシミュレーションし、結果のヒストグラムを表示します。

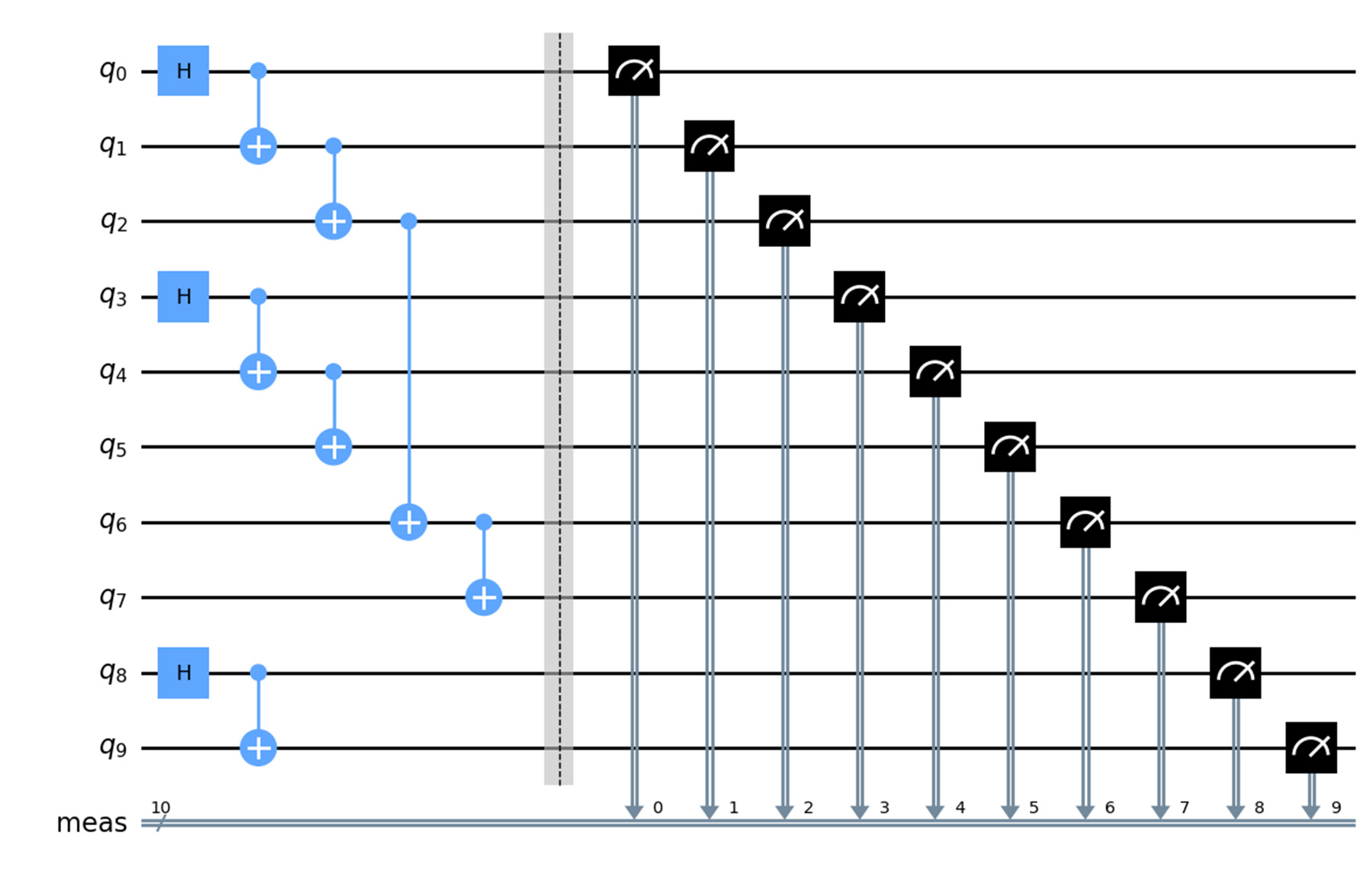
このコードを詳しく見ていくと、 q[0] から q[2] までと q[6]、 q[7] がエンタングルし、加えて q[3] から q[5] まで、そして q[8] と q[9] がそれぞれエンタングルしていることがわかる。したがって、その測定結果は、10ビット1024種類の中から、以下のような8つのパターンだけが、それぞれほぼ同じ確率で現れる。

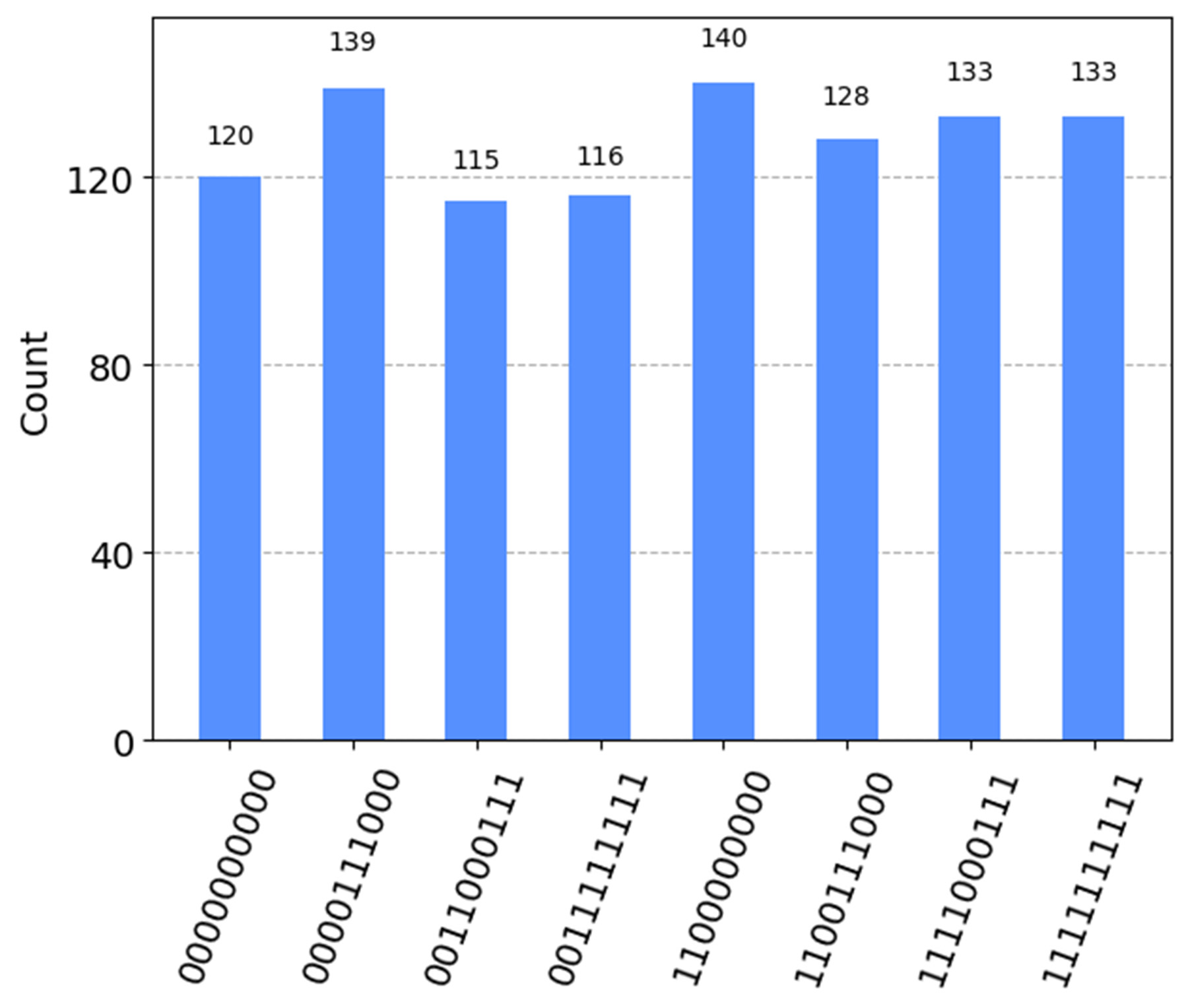
もつれ構造を作り出す別の方法

次に、こうしたアダマールゲートとCNOTゲートを用いる以外の方法について質問してみる。

すると以下のような、10通りの方法が示された。

1. 別のゲートの使用：
   CNOTゲートやアダマールゲート以外にも、トフォリゲート、フレドキンゲート、コントロールUゲートといった量子ゲートを用いて複雑なエンタングルメント構造を作ることができます。マルチ量子ビット・ゲートは、複数の量子ビットを自明でない方法で同時にもつれさせることができます。
2. 量子回路設計：
   異なるトポロジーやゲートシーケンスで回路を設計することで、さまざまなもつれ構造を作り出すことができます。例えば、量子ビットを格子状に配置し、幾何学的パターンに基づいたゲートを適用することで、複雑なもつれ構造を作り出すことができます。
3. 量子アルゴリズムの利用：
   ある種の量子アルゴリズムは、その動作の一部として複雑なエンタングルメント構造を自然に作り出します。例えば、ある組合せ問題を解くための量子アルゴリズムや、量子システムをシミュレートするための量子アルゴリズムは、複雑なエンタングルメントを生成する可能性があります。
4. パラメータ化された量子回路（PQC）：
   PQCは、ゲートのパラメータを最適化できる変数とした量子回路です（それゆえ量子ニューラルネットとも呼ばれます）。PQCのパラメータを最適化することで、さまざまなエンタングルメント構造を作成・探索することができます。
5. 量子コンパイラとオプティマイザ：
   量子コンパイラとオプティマイザは、量子回路の再配列と単純化を行うことができ、その過程で複雑なエンタングルメント構造を作り出せる可能性があります。高度なコンパイル技術により、目的の量子計算を実現する、自明でないエンタングルメント構造を発見できるかもしれません。
6. アンシラ量子ビットの使用：
   アンシラ（ancilla）量子ビットは、量子計算を容易にするために使用される補助的な量子ビットです。この追加の量子ビットをマルチ量子ビット演算の仲介役として使用することで、より複雑なエンタングルメント構造を作り出すことができます。
7. ハイブリッド量子ー古典アルゴリズム：
   変分量子固有値解法（VQE）^※5や量子近似最適化アルゴリズム（QAOA）^※6のようなアルゴリズムは、量子処理と古典処理を組み合わせて問題を解きます。これらのアルゴリズムの量子部分は、複雑なもつれ構造を作り出すことができ、それを古典最適化ループで使用します。
8. 誤り訂正符号：
   量子エラー訂正符号^※7は、エラーの検出と訂正に複雑な多量子ビットのもつれを必要とすることが多くあります。誤り訂正符号を設計・実装することは、複雑なエンタングルメント構造を作り出すことにつながります。
9. モジュラー量子回路：
   量子回路をモジュール方式で設計し、より小さなもつれのサブ回路を組み合わせて、より大きな回路を形成することで、複雑なもつれ構造を作り出すことができます。
10. 量子グラフ状態の探索：
    量子グラフ^※8状態は、数学的なグラフに対応するもつれ状態の一種で、頂点は量子ビットを、辺はもつれを表しています。特定のグラフ状態を作り出す回路を設計することで、さまざまかつ複雑なエンタングルメント構造を作り出すことができます。

実際にこれらの方法のいくつかをコードで示してもらった。

1. 別のゲートの使用：

トフォリゲート（CNOTゲートを3量子ビットに拡張したもの）とフレドキンゲート（制御SWAPゲート）を使って、より複雑なエンタングルメント構造を作る例です。

from qiskit import QuantumCircuit, Aer, transpile
from qiskit.visualization import plot_histogram
from qiskit.providers.aer import AerSimulator

# Create a quantum circuit
circuit = QuantumCircuit(5)

# Apply Toffoli and Fredkin gates
circuit.h(0)
circuit.ccx(0, 1, 2)  # Toffoli gate
circuit.fredkin(1, 3, 4)  # Fredkin gate

# Measure the qubits
circuit.measure_all()

# Simulate the circuit
simulator = AerSimulator()
compiled_circuit = transpile(circuit, simulator)
result = simulator.run(compiled_circuit).result()
counts = result.get_counts()
plot_histogram(counts)

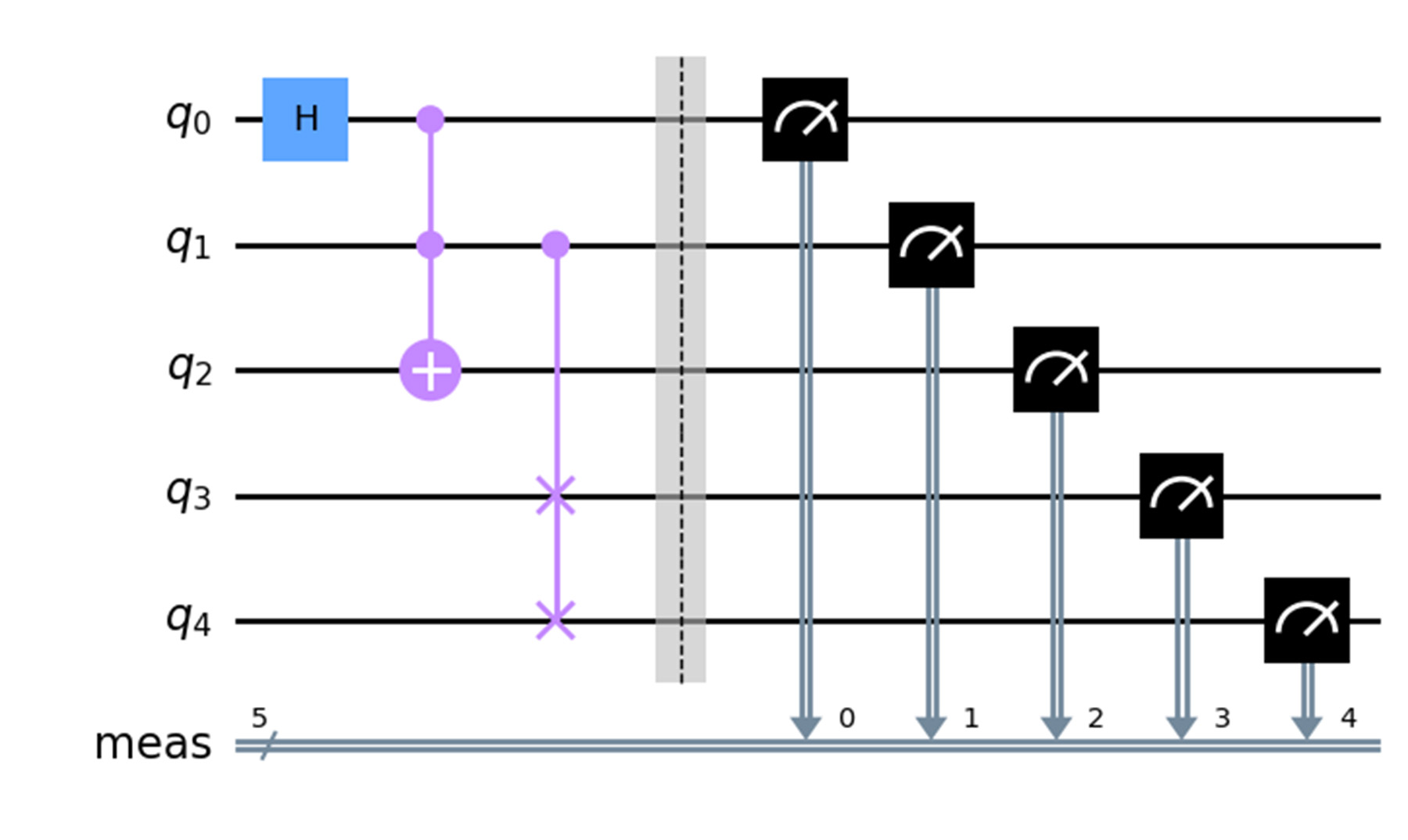
この量子回路は、一見複雑に見えるが、q[0]だけが重ね合わせ状態なので、0と1が半々の確率で現れ、それ以外は常に0のままである。

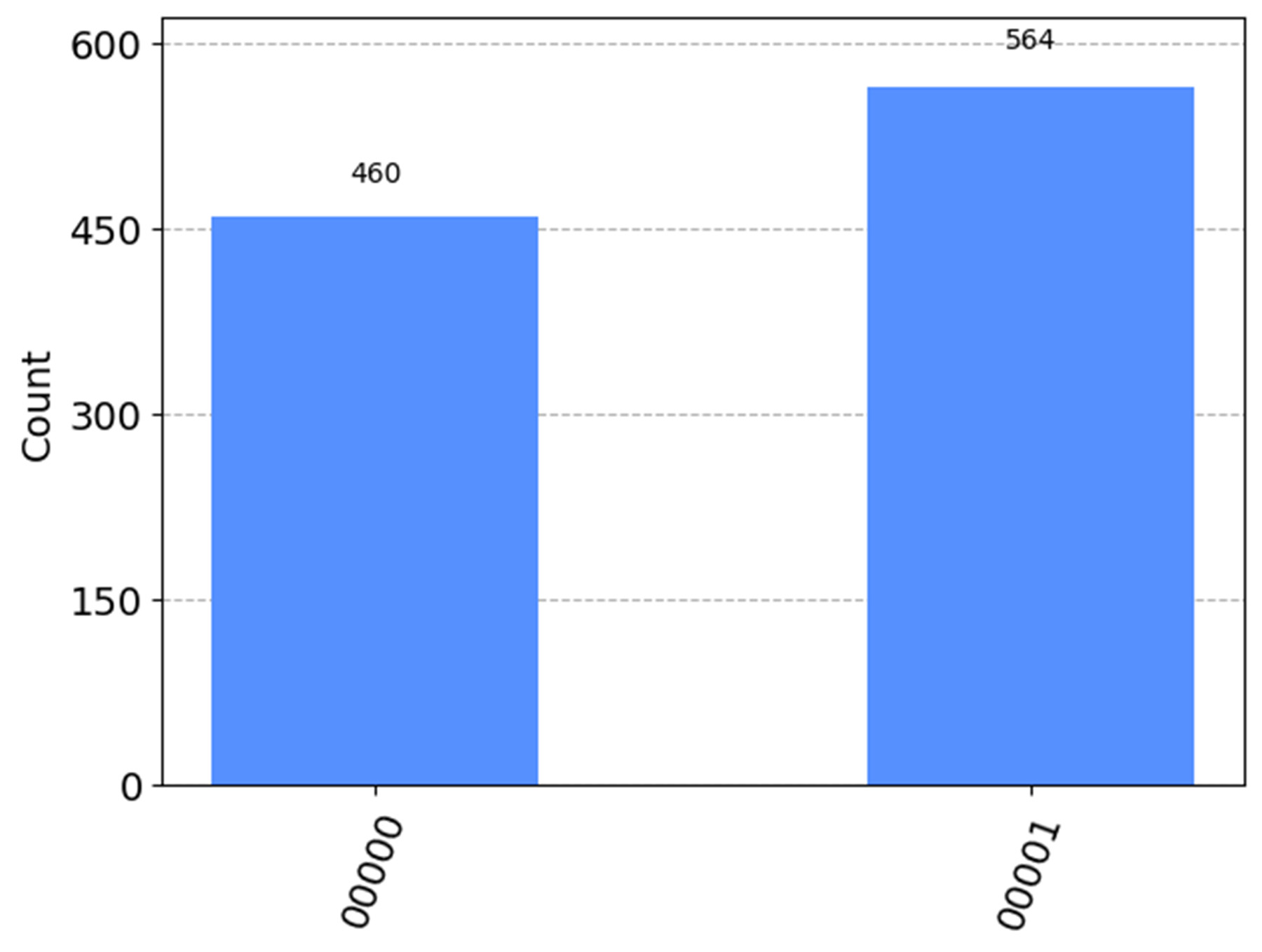
2. 量子回路設計：

別のトポロジーを持つ回路を設計してみます。

from qiskit import QuantumCircuit, Aer, transpile
from qiskit.visualization import plot_histogram

from qiskit.providers.aer import AerSimulator

# Create a quantum circuit
circuit = QuantumCircuit(4)

# Apply a sequence of gates
circuit.h(0)
circuit.cx(0, 1)
circuit.cx(1, 2)
circuit.h(2)
circuit.cx(2, 3)
circuit.h(3)

# Measure the qubits
circuit.measure_all()

# Simulate the circuit
simulator = AerSimulator()
compiled_circuit = transpile(circuit, simulator)
result = simulator.run(compiled_circuit).result()
counts = result.get_counts()
plot_histogram(counts)

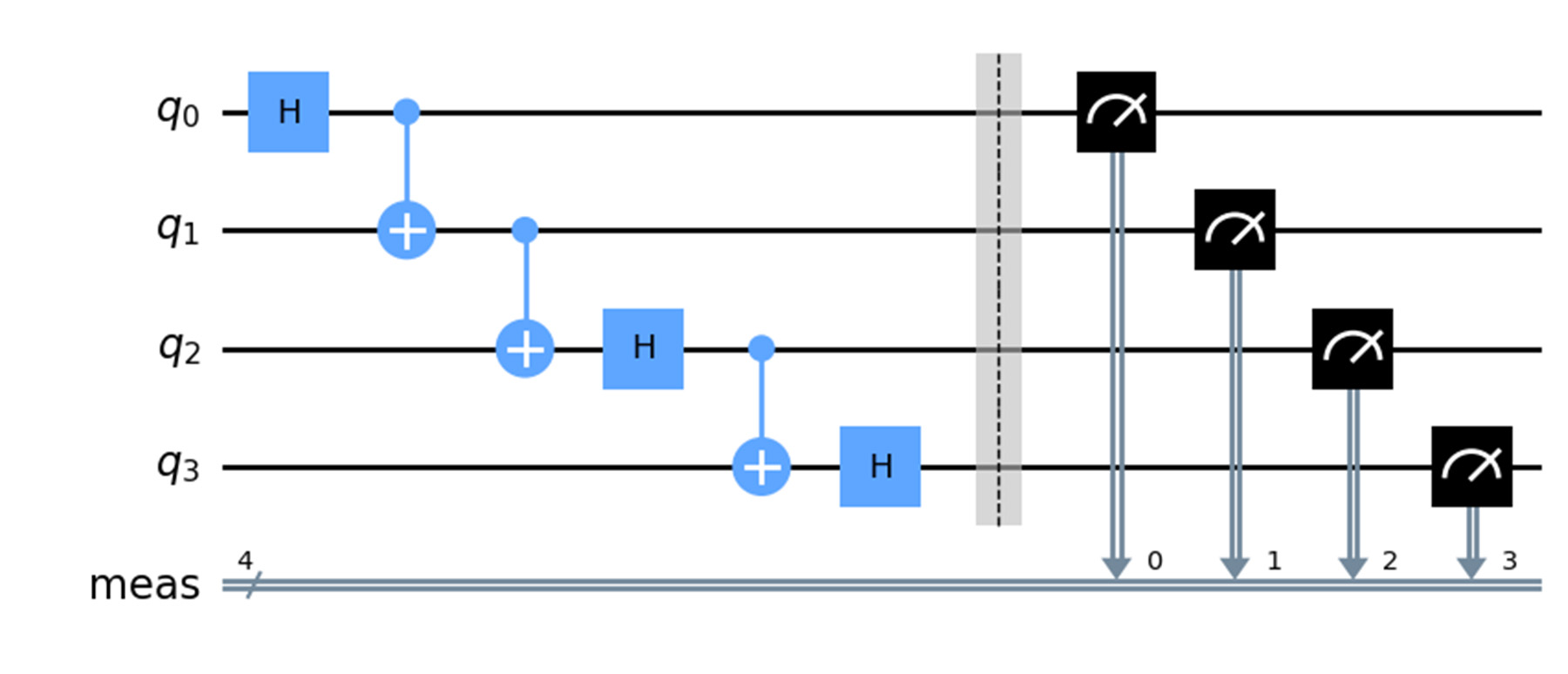
この量子回路は、q[0]からq[2]までがエンタングルしたにもかかわらず、その後q[2]とq[3]が重ね合わせの状態になるので、この2つの量子ビットの測定結果（上位2ビット）には0と1がほぼ均等に現れる。

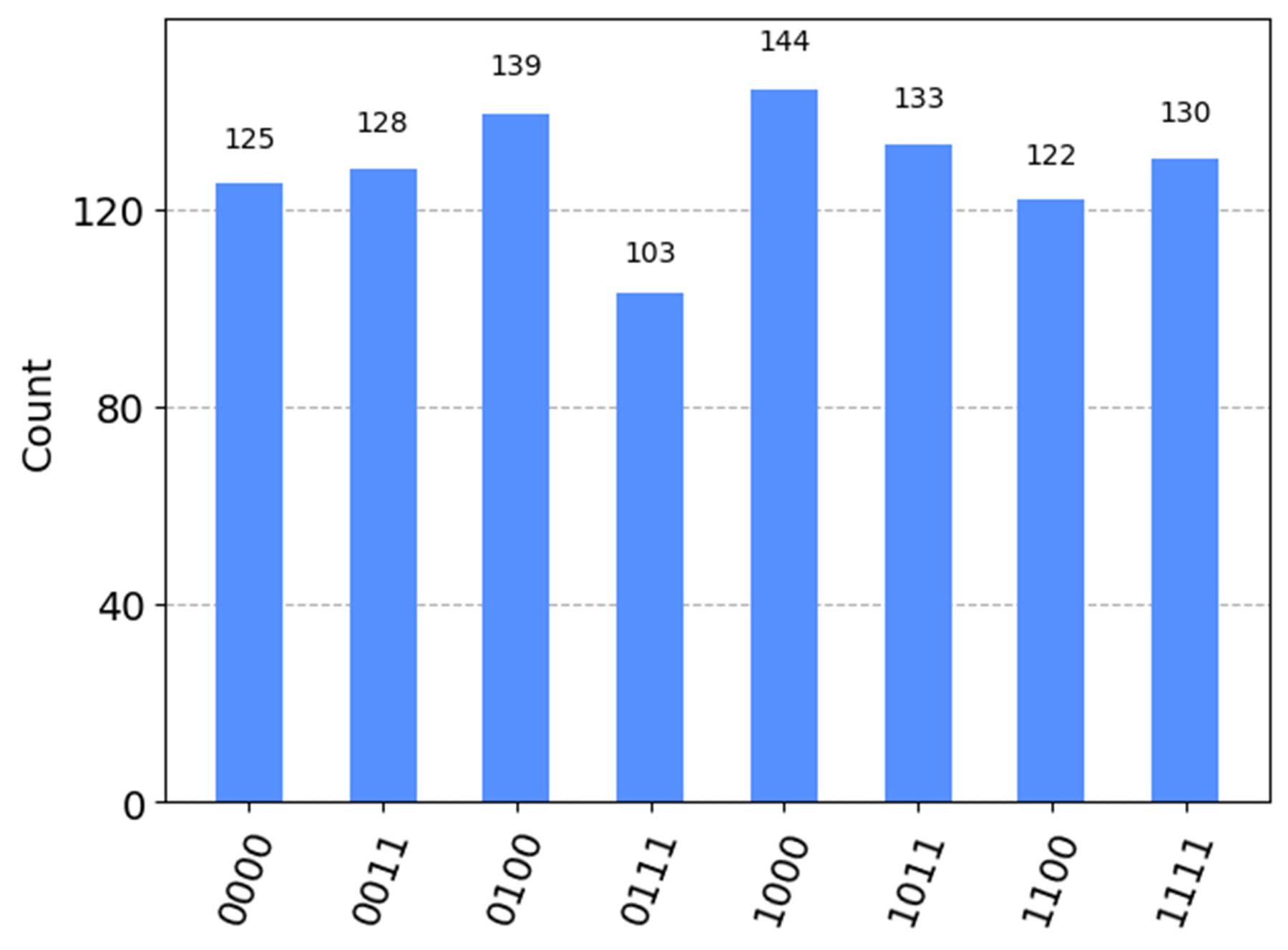
3. パラメータ化された量子回路（PQC）：

可変ゲートパラメータを持つPQCを作成してみます。

from qiskit import QuantumCircuit, Aer, transpile
from qiskit.visualization import plot_histogram
from qiskit.providers.aer import AerSimulator
from qiskit.circuit import Parameter
import math

# Define parameters
theta = Parameter('θ')
phi = Parameter('ϕ')

# Create a parameterized quantum circuit
pqc = QuantumCircuit(2)
pqc.rx(theta, 0)
pqc.ry(phi, 1)
pqc.cx(0, 1)

# Measure the qubits
pqc.measure_all()

# bind the parameters after circuit to create a bound circuit
bc = pqc.bind_parameters({theta: math.pi/4, phi: math.pi/2})

# Simulate the bound circuit
simulator = AerSimulator()
compiled_circuit = transpile(bc, simulator)
result = simulator.run(compiled_circuit).result()
counts = result.get_counts()
plot_histogram(counts)

Rxゲート（x軸回転ゲート）とRyゲート（y軸回転ゲート）の回転量（thetaとphi）をパラメータ（変数）とし、実行前にパラメータを束縛する（変数の値を決める）ことで、ダイナミックな量子回路を設計することができる。

パラメータの束縛前（pqc）

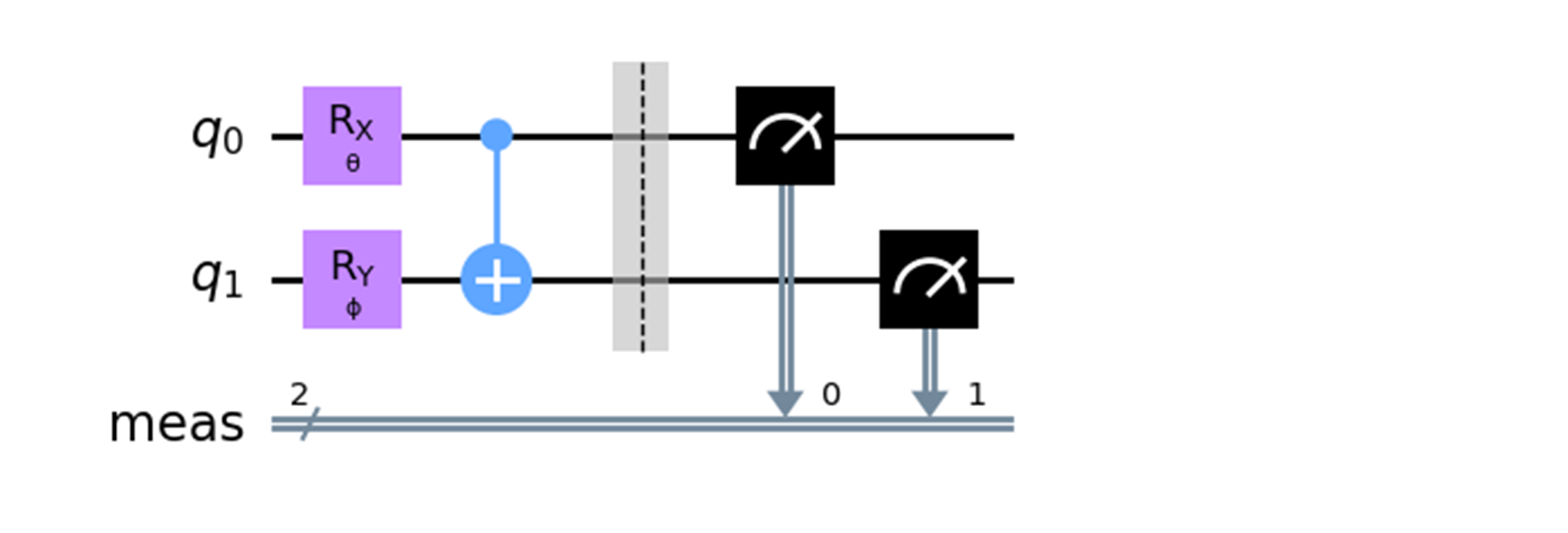
パラメータの束縛後（bc）［theta=π/4, phi=π/2］

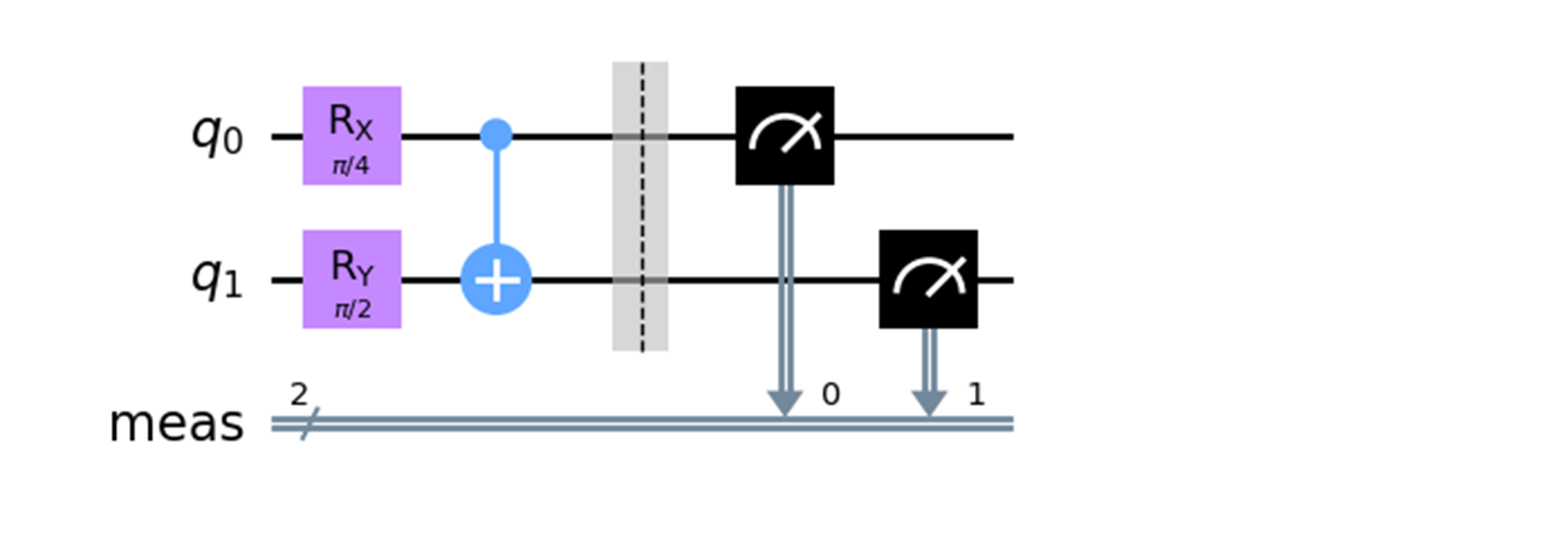
測定結果は以下のようになる。

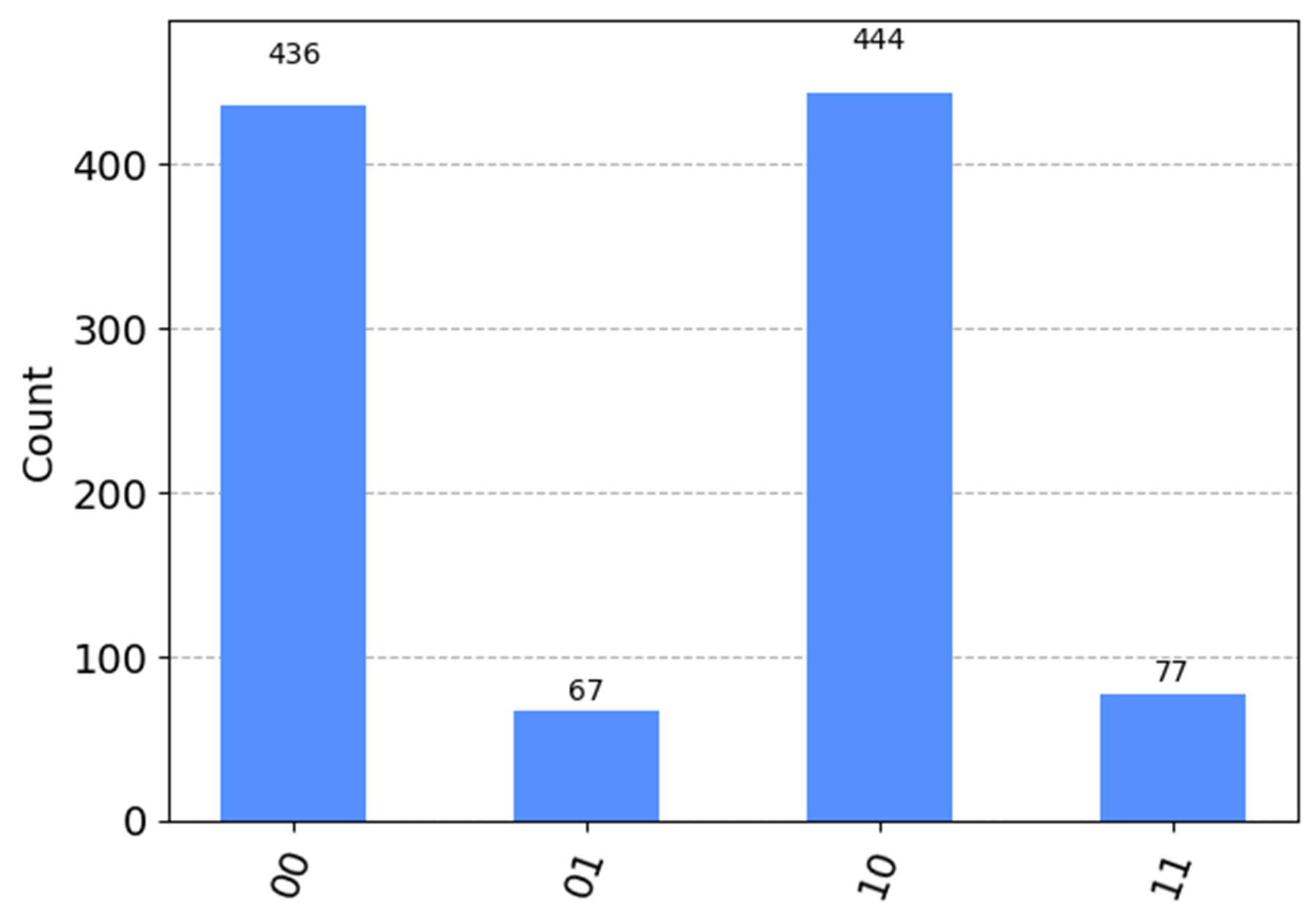
以下の1行でパラメータを変化させる［theta=3π/4, phi=π/3］ことで、確率分布を変化させることができる。

# bind the parameters after circuit to create a bound circuit
bc = pqc.bind_parameters({theta: 3*math.pi/4, phi: math.pi/3})

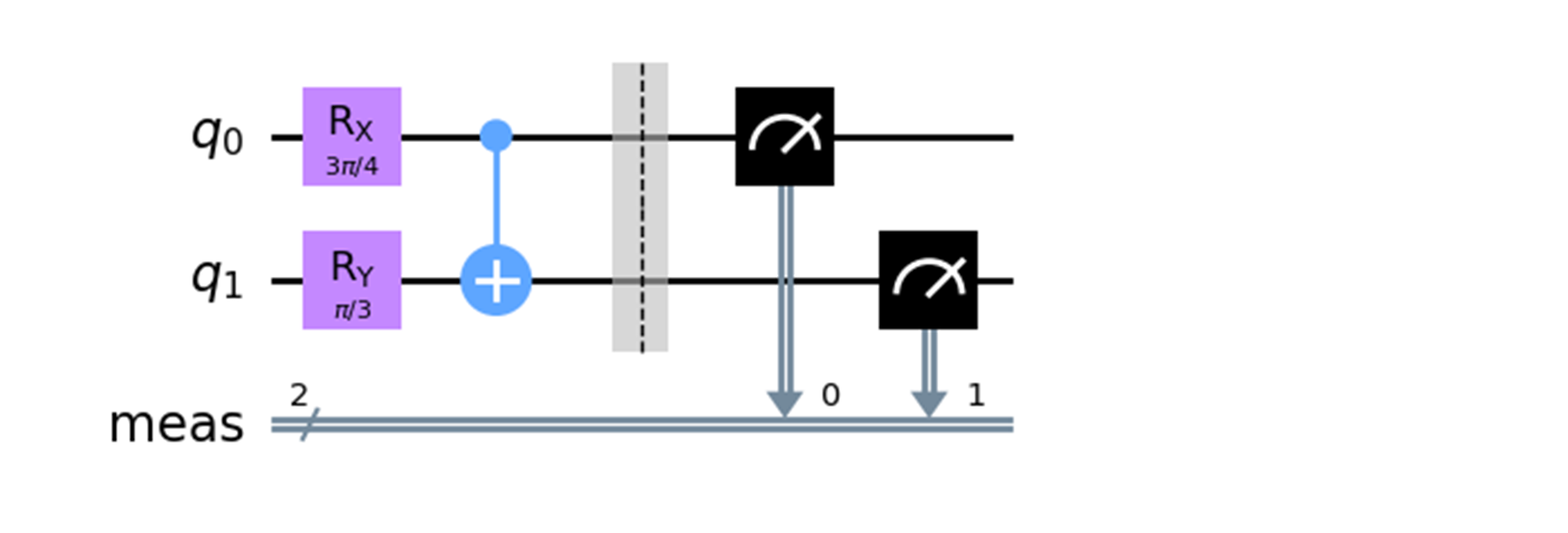
測定結果は以下のようになる。

4. モジュラー量子回路：

小さな回路を組み合わせて、より大きな回路を形成します。

from qiskit import QuantumCircuit, Aer, transpile
from qiskit.visualization import plot_histogram
from qiskit.providers.aer import AerSimulator

# Define two smaller circuits
sub_circuit1 = QuantumCircuit(2)
sub_circuit1.h(0)
sub_circuit1.cx(0, 1)

sub_circuit2 = QuantumCircuit(2)
sub_circuit2.h(1)
sub_circuit2.cx(1, 0)

# Combine the smaller circuits to form a larger circuit
combined_circuit = QuantumCircuit(4)  # Create a new circuit with enough qubits
combined_circuit.compose(sub_circuit1, [0, 1], inplace=True)
combined_circuit.compose(sub_circuit2, [2, 3], inplace=True)

# Measure the qubits
combined_circuit.measure_all()

# Simulate the circuit
simulator = AerSimulator()
compiled_circuit = transpile(combined_circuit, simulator)
result = simulator.run(compiled_circuit).result()
counts = result.get_counts()
plot_histogram(counts)

sub_circuit1：

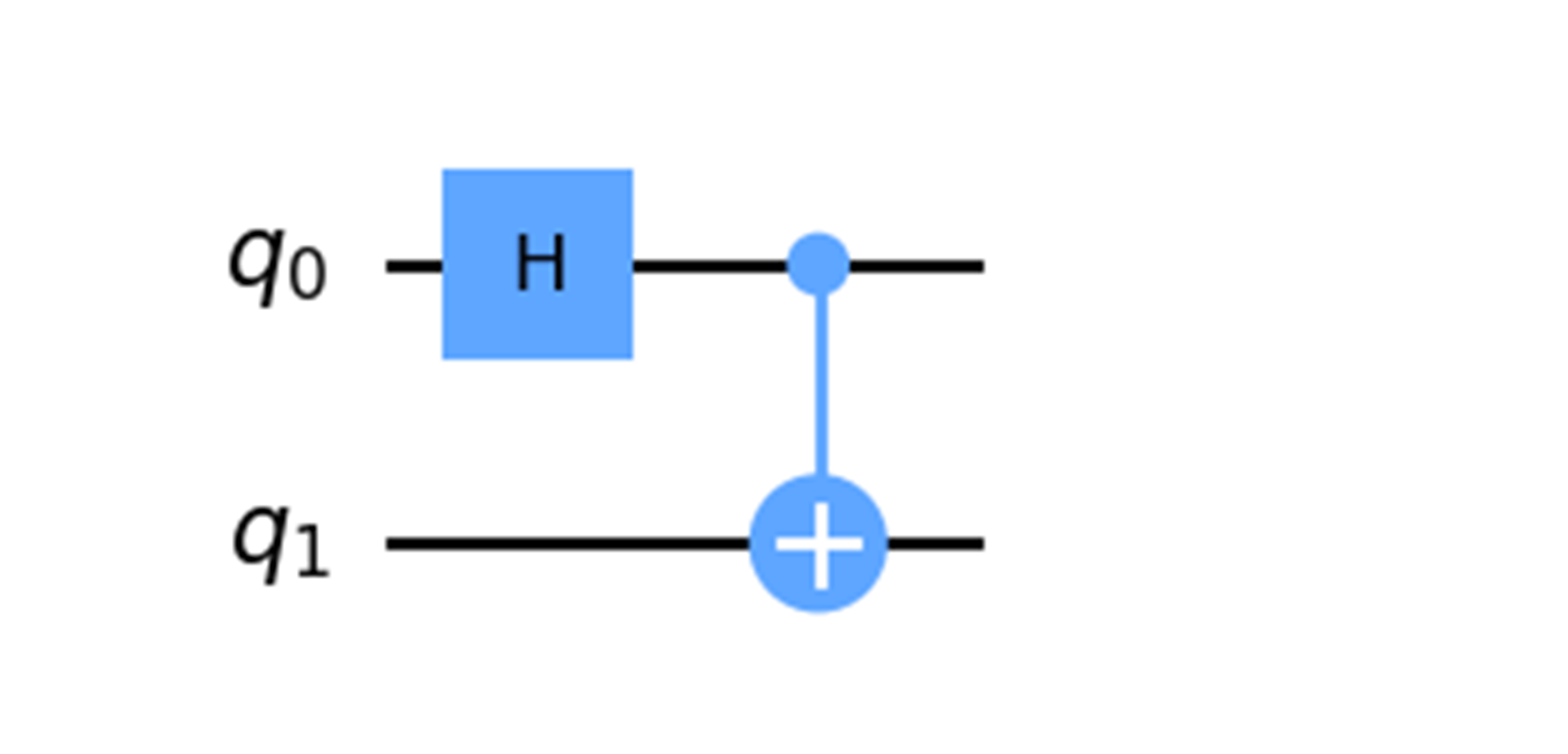
sub_circuit2：

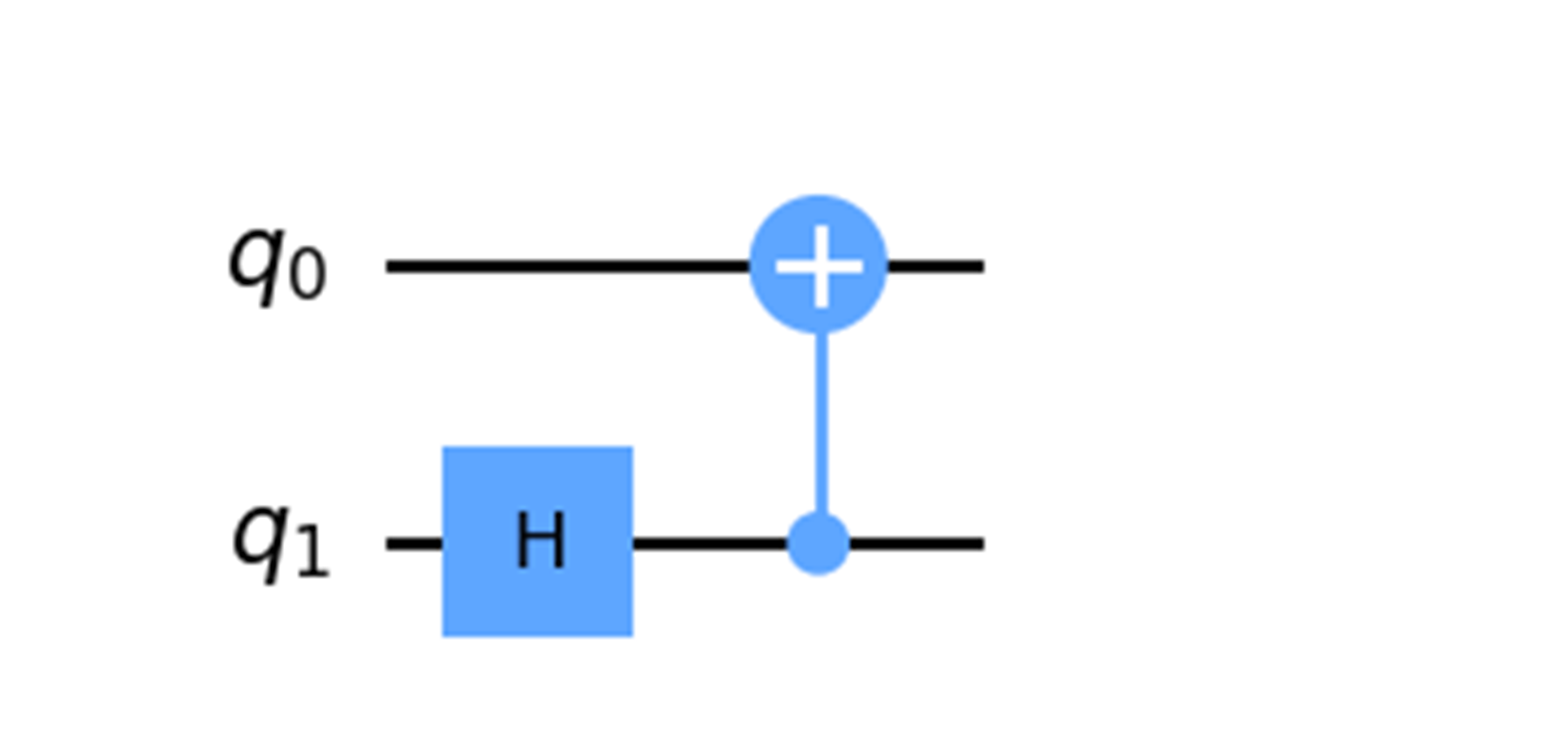
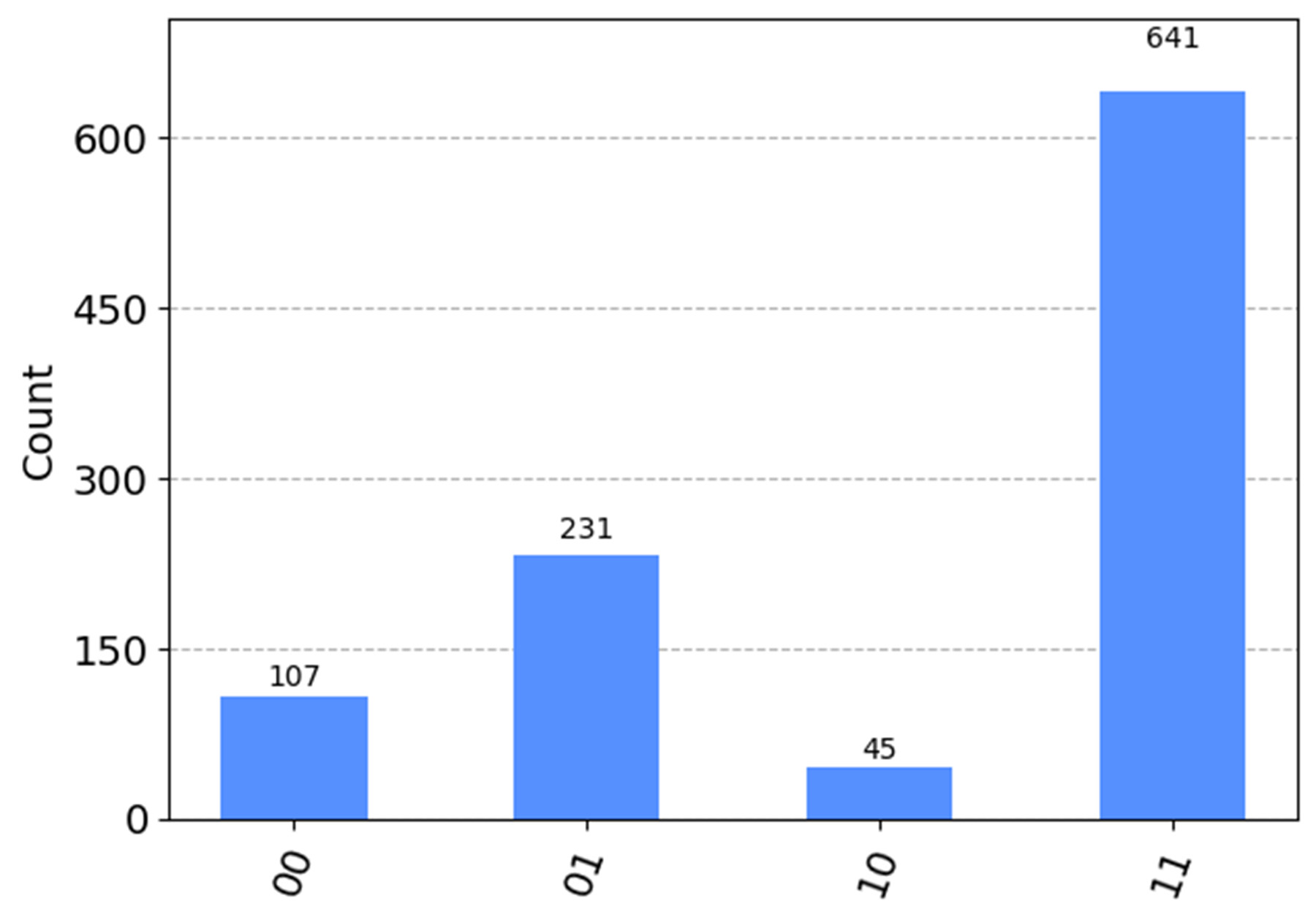
この2つのサブ回路を組み合わせた量子回路（combined_circuit）

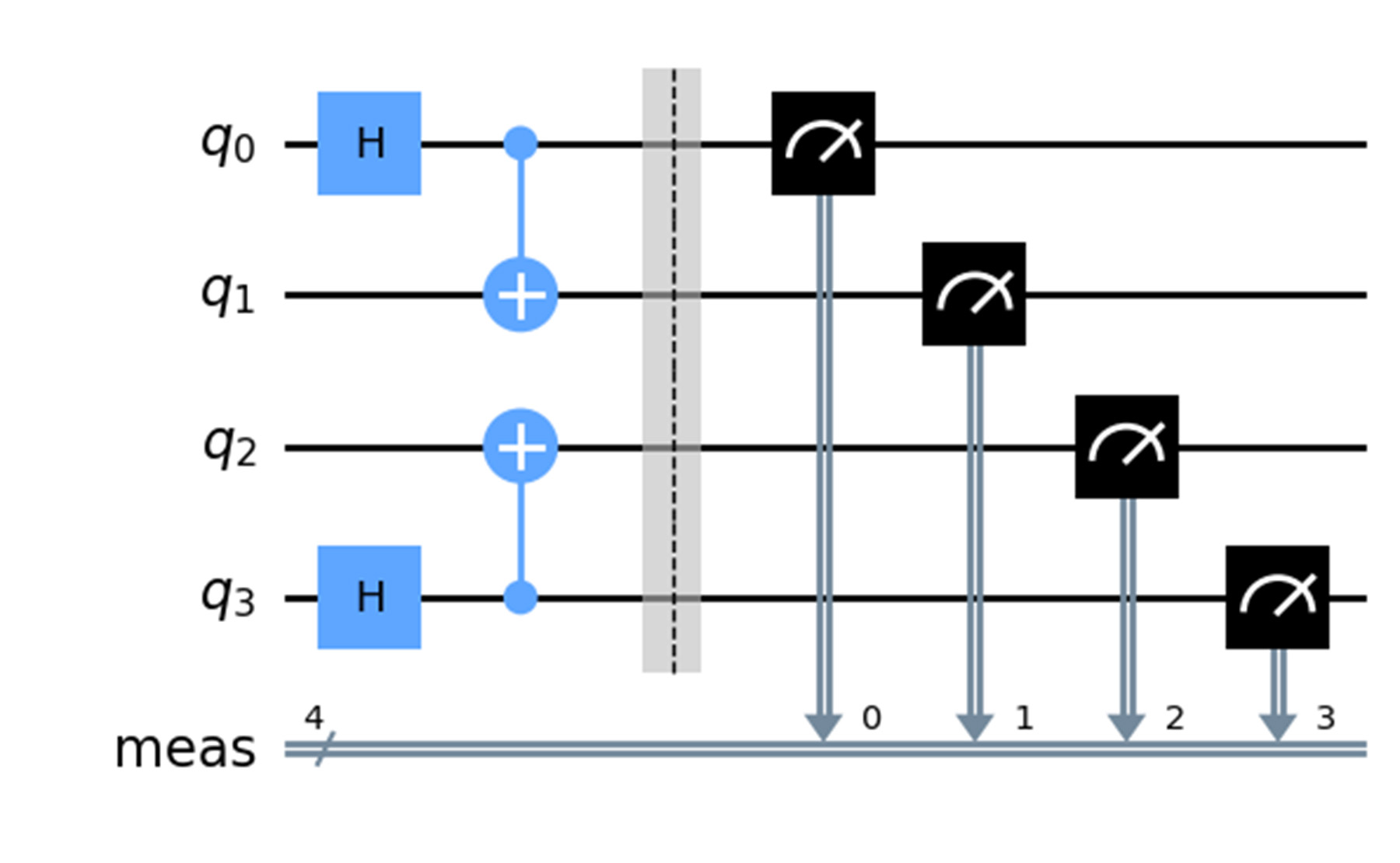
サブ回路の組み合わせ方は自由である。以下の部分を変えると2つのサブ回路が互い違いに結合する。

# Combine the smaller circuits to form a larger circuit
combined_circuit = QuantumCircuit(4)  # Create a new circuit with enough qubits
combined_circuit.compose(sub_circuit1, [0, 2], inplace=True)
combined_circuit.compose(sub_circuit2, [1, 3], inplace=True)

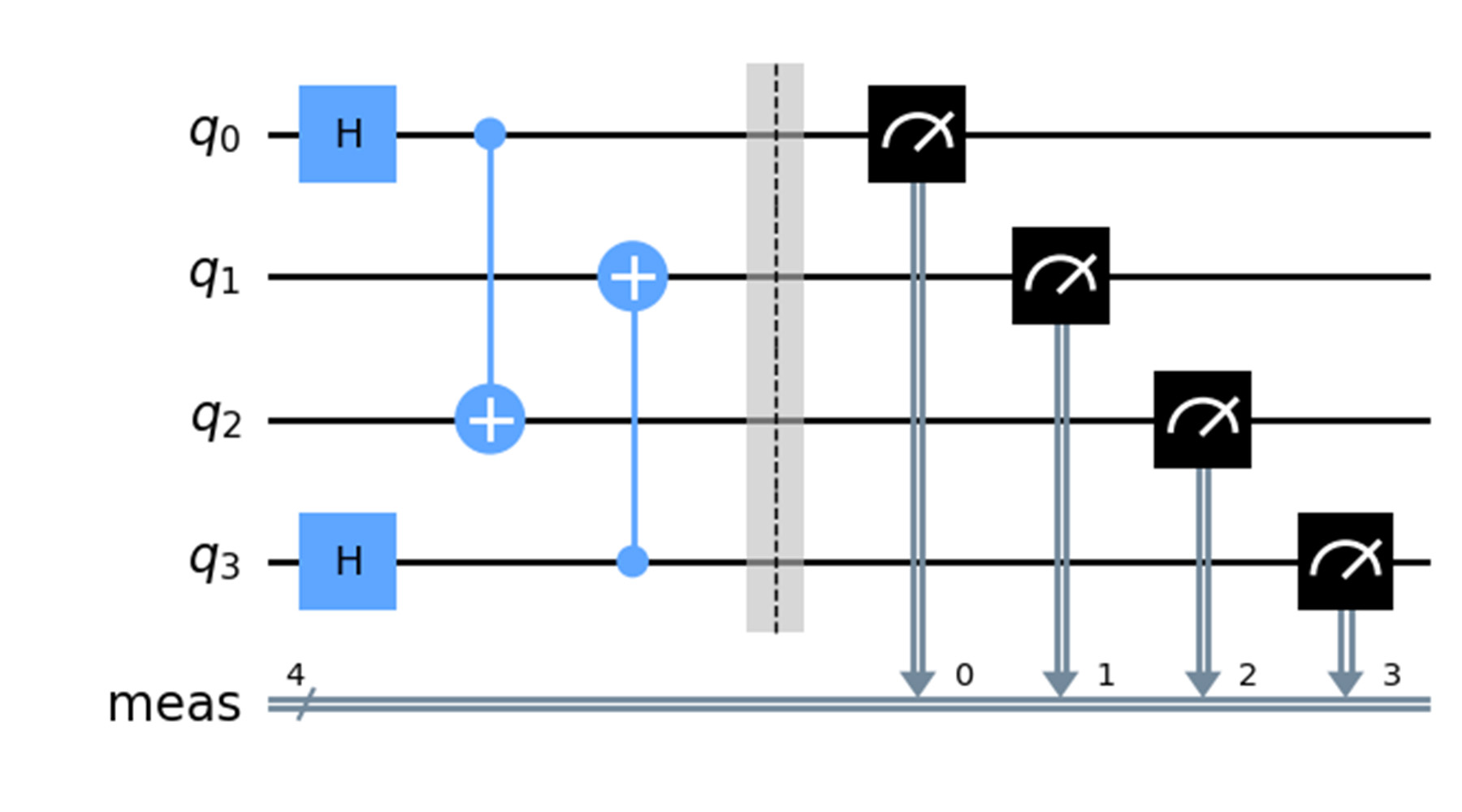
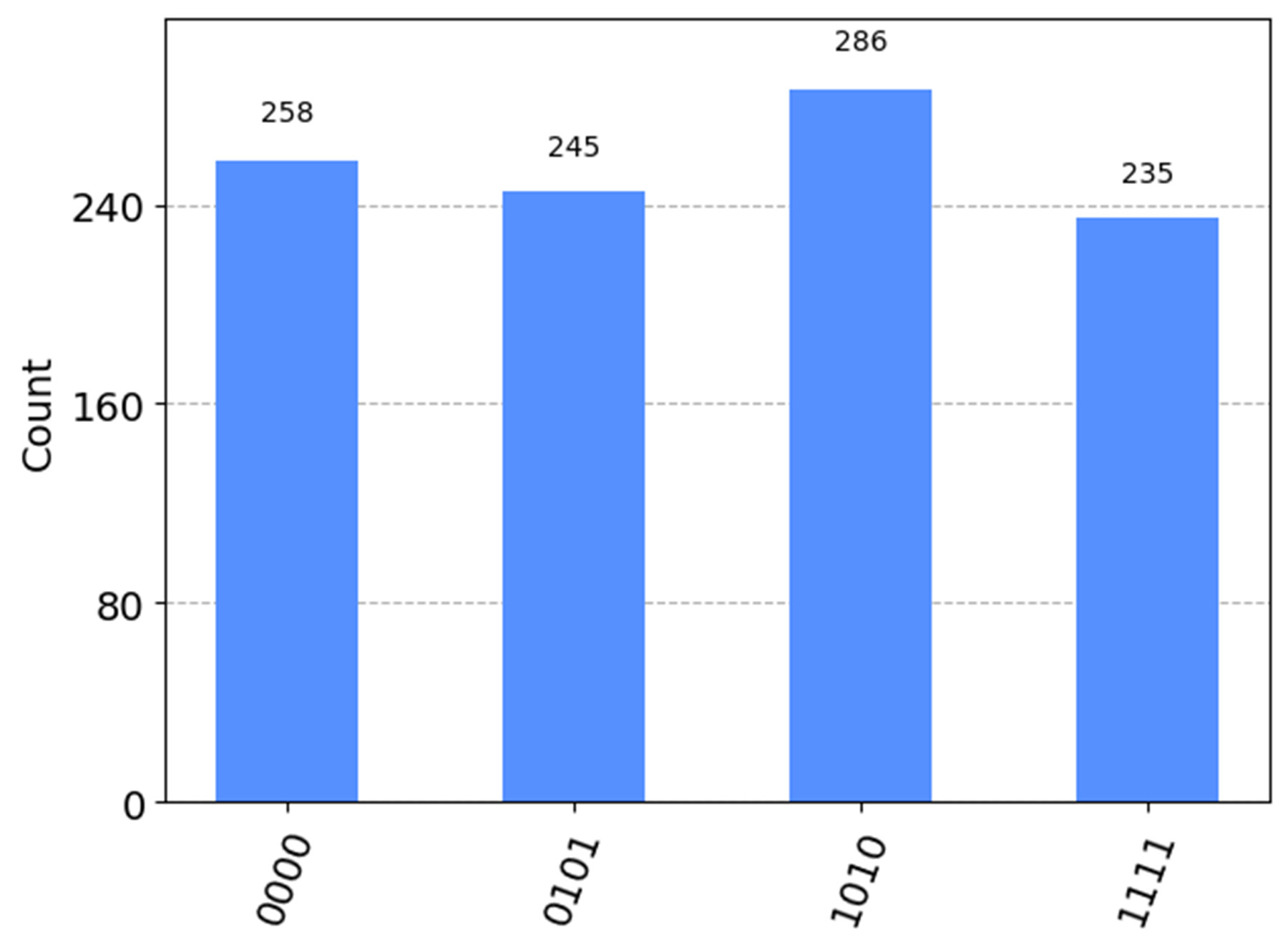
この回路の測定結果は以下のようになる。q[0]とq[2]、q[1]とq[3]がエンタングルしている。

こうした複合ゲートや、パラメータ化された回路については、Qiskitのチュートリアル「高度な回路^※9」により詳細な解説がある。

エンタングルメントと測定の繰り返し

さらに、本稿で紹介した量子テレポーテーションのように、エンタングルメントと測定が交互に現れる例について聞いてみる。

from qiskit import QuantumCircuit, Aer, transpile, assemble
from qiskit.providers.aer import AerSimulator
from qiskit.visualization import plot_histogram

# Create a quantum circuit with 9 qubits and 3 classical bits
circuit = QuantumCircuit(9, 3)

# Initial entanglement
circuit.h(0)
circuit.cx(0, 1)

# Measurement and conditional operation
circuit.measure(1, 0)
circuit.x(2).c_if(circuit.clbits[0], 1)

# Further entanglement
circuit.h(3)
circuit.cx(3, 4)

# Measurement and conditional operation
circuit.measure(4, 1)
circuit.x(5).c_if(circuit.clbits[1], 1)

# Further entanglement
circuit.h(6)
circuit.cx(6, 7)

# Measurement and conditional operation
circuit.measure(7, 2)
circuit.x(8).c_if(circuit.clbits[2], 1)

# Simulate the circuit
simulator = AerSimulator()
compiled_circuit = transpile(circuit, simulator)
result = simulator.run(compiled_circuit).result()
counts = result.get_counts()
plot_histogram(counts)

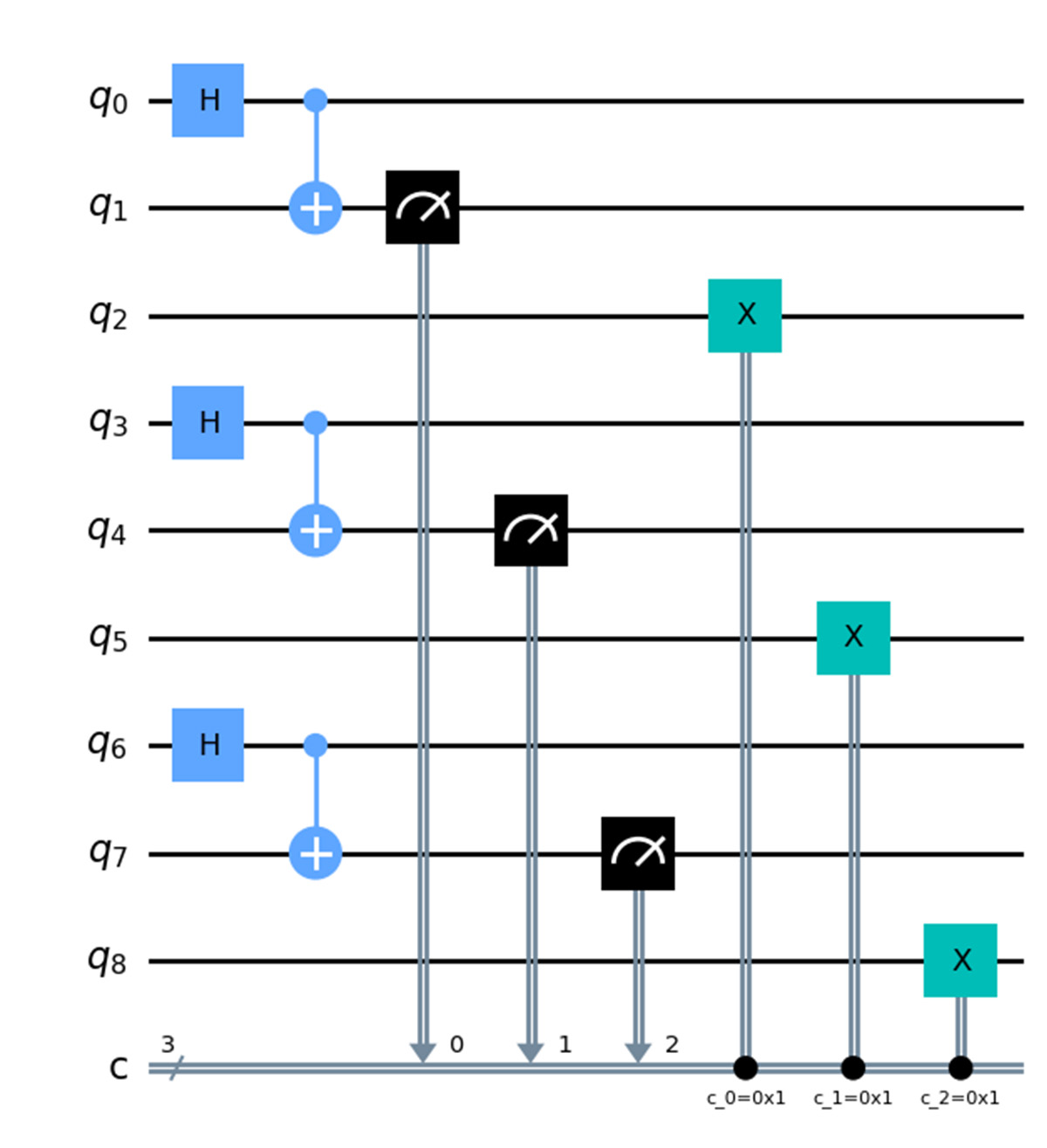
この回路の q[1] q[4] q[7] の測定結果は、以下のようになるが、エンタングルによってq[0] q[3] q[6]の値も同時に決まる。これらの測定結果によって、q[2] q[5] q[8]の量子状態（Xゲートの適用の有無）が決まる。

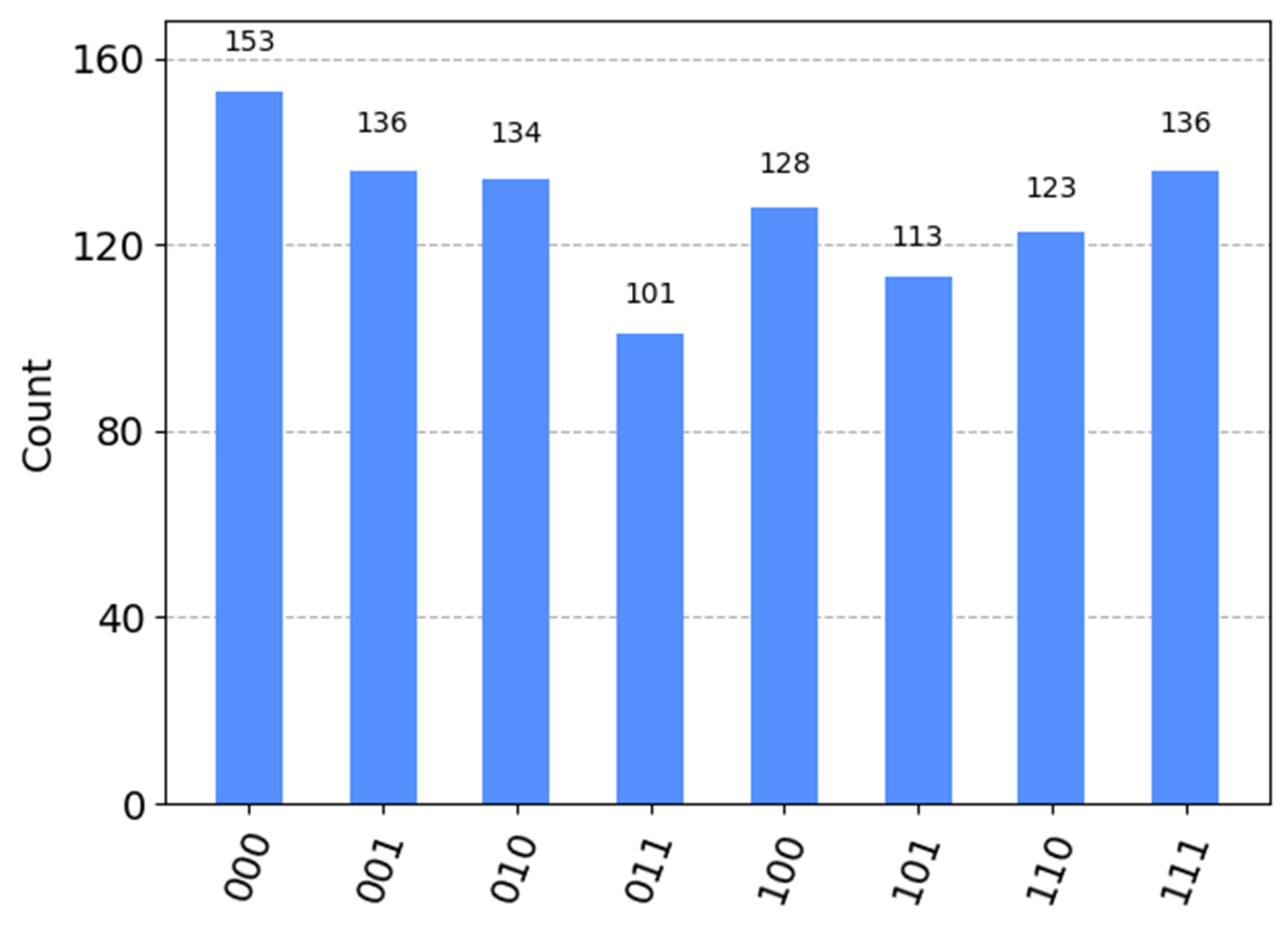
同様の例として、以下のようなものも示された。

from qiskit import QuantumCircuit, Aer, transpile, assemble
from qiskit.providers.aer import AerSimulator
from qiskit.visualization import plot_histogram

# Create a quantum circuit with 6 qubits and 3 classical bits
circuit = QuantumCircuit(6, 3)

# Initial entanglement
circuit.h(0)
circuit.cx(0, 1)

# Measurement and conditional operation
circuit.measure(1, 0)
circuit.x(2).c_if(circuit.clbits[0], 1)

# Further entanglement
circuit.h(2)
circuit.cx(2, 3)

# Measurement and conditional operation
circuit.measure(3, 1)
circuit.x(4).c_if(circuit.clbits[1], 1)

# Further entanglement
circuit.h(4)
circuit.cx(4, 5)

# Final measurement
circuit.measure(5, 2)

# Simulate the circuit
simulator = AerSimulator()
compiled_circuit = transpile(circuit, simulator)
result = simulator.run(compiled_circuit).result()
counts = result.get_counts()
plot_histogram(counts)

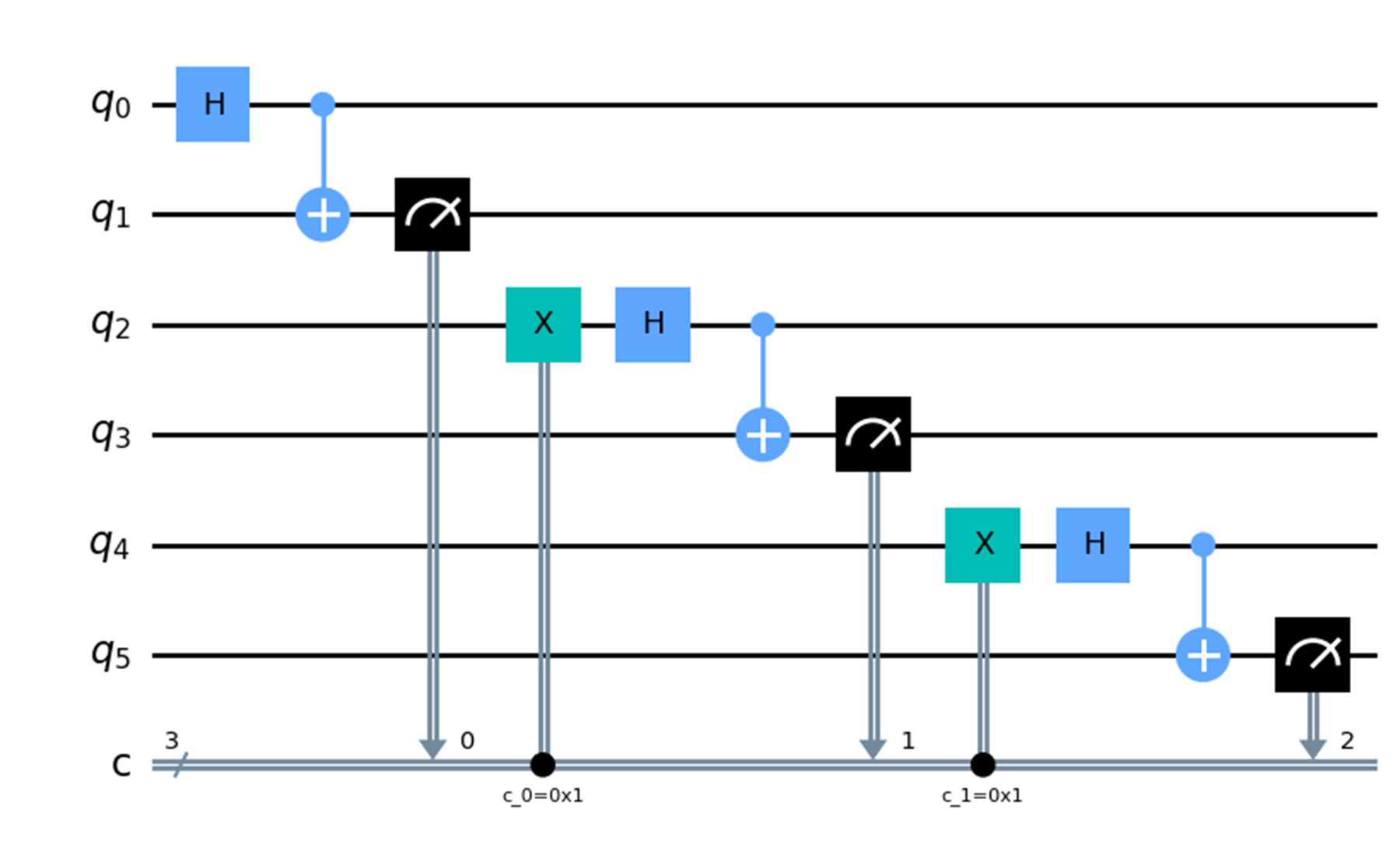
先の例が、3つのサブ回路が並列に結合していたのに対し、この例では「アダマールゲート→CNOTによるエンタングルメント→測定→測定結果によってXゲートを適用」というパターンをずらしながら直列に繋いでいく。このコードの内容をChatGPTにも尋ねてみた。

なお、q[1] q[3] q[5] の測定結果は以下の通りである。

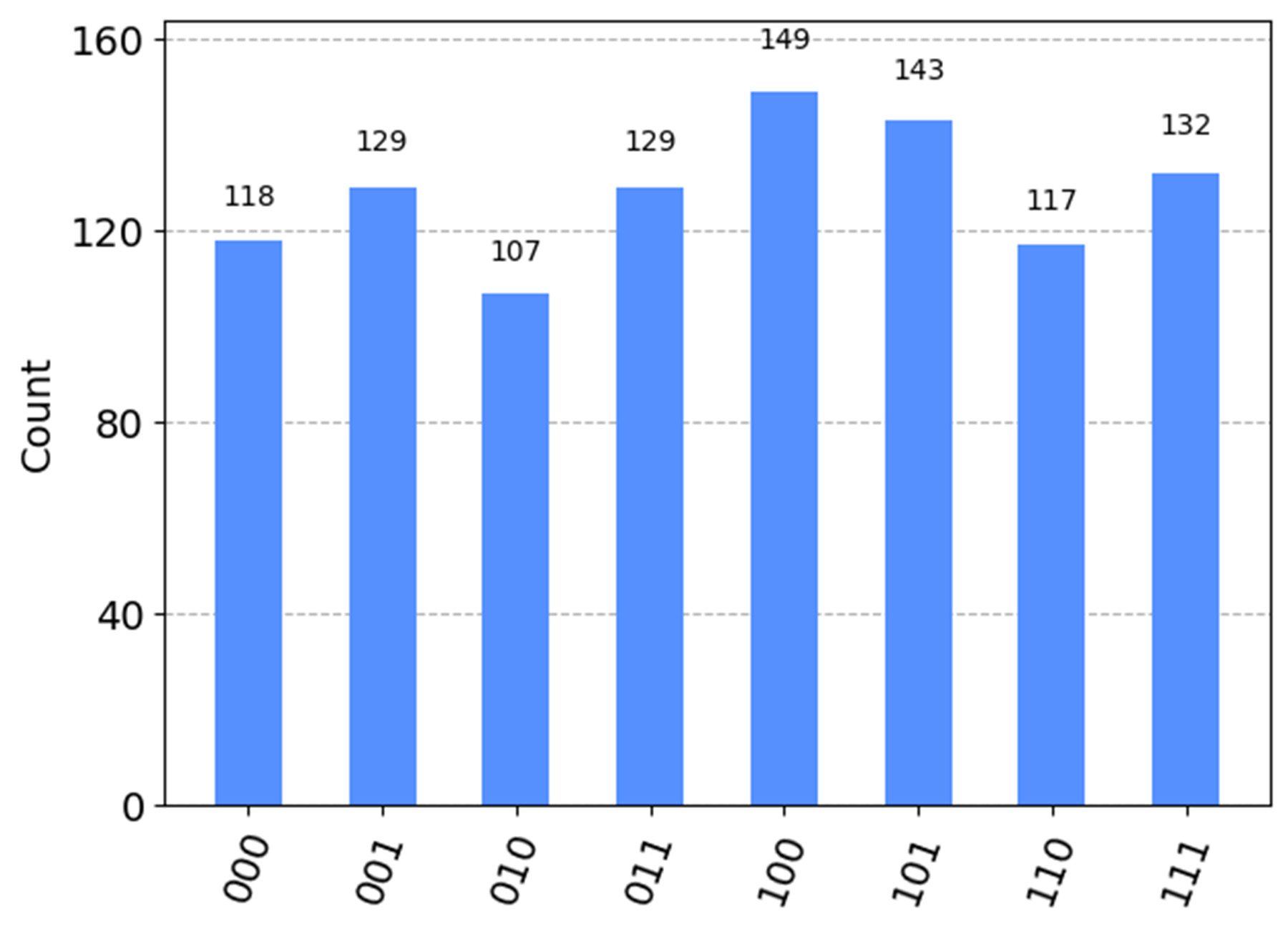
量子回路のパラメトリックな生成

先ほど、パラメータ化した量子回路の例が示されたが、さらに量子回路のトポロジーそのものを、パラメータ化することもできる。例えば、以下のように乱数によってCNOTやCZゲートのトポロジーを決めてみる。

from qiskit import QuantumCircuit, Aer, transpile, assemble
from qiskit.providers.aer import AerSimulator
from qiskit.visualization import plot_histogram
import numpy as np
import random

qc = QuantumCircuit(5)

for k in range(3):
    i = random.randint(0, 4)
    j = random.randint(0, 4)
    if (i!=j):
        qc.cx(i, j)
    qc.h(random.randint(0, 4))
    i = random.randint(0, 4)
    j = random.randint(0, 4)
    if (i!=j):
        qc.cz(i, j)

# Measure all qubits
qc.measure_all()

# Simulate the circuit
simulator = AerSimulator()
compiled_circuit = transpile(qc, simulator)
result = simulator.run(compiled_circuit).result()
    counts = result.get_counts()
plot_histogram(counts)

このコードの内容は、

で、例えば以下のような量子回路を生成する。

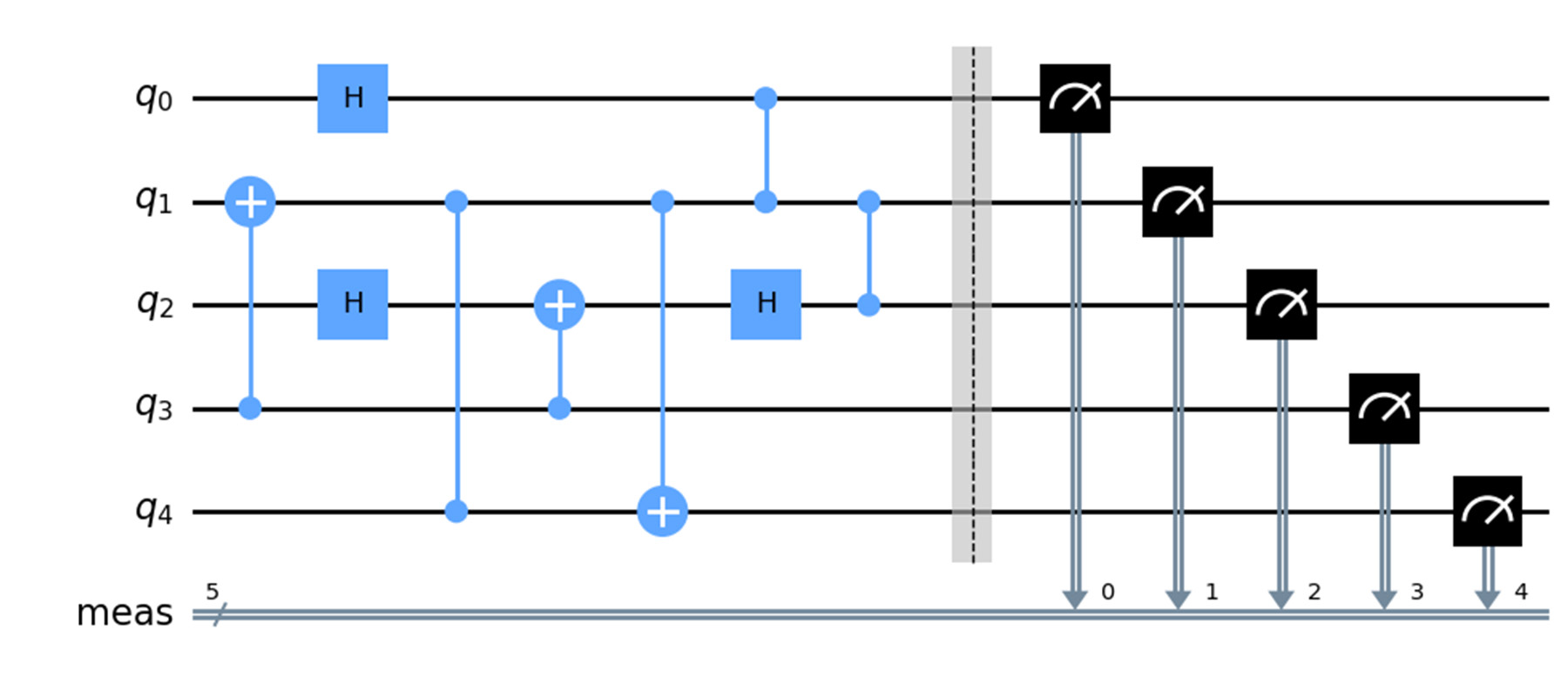
なお、測定結果はすべて00000となる。

こうしたランダムなトポロジー生成を繰り返せば、いくらでも複雑な量子回路が生成できる。例えば、プログラムの繰り返し回数を20回にすると、以下のような量子回路が生成される。

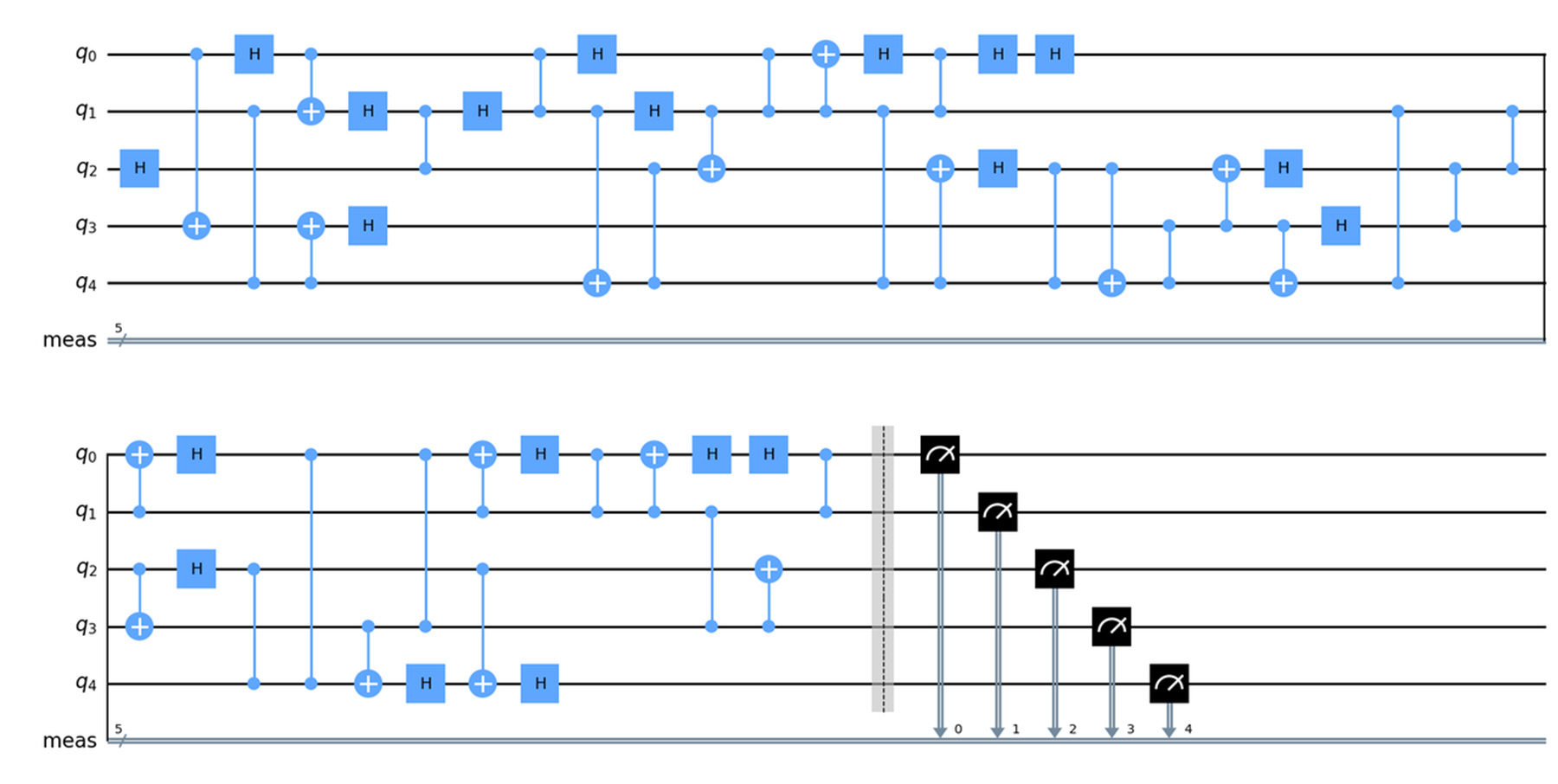
この測定結果は、以下のような特徴的なパターンを持っている。

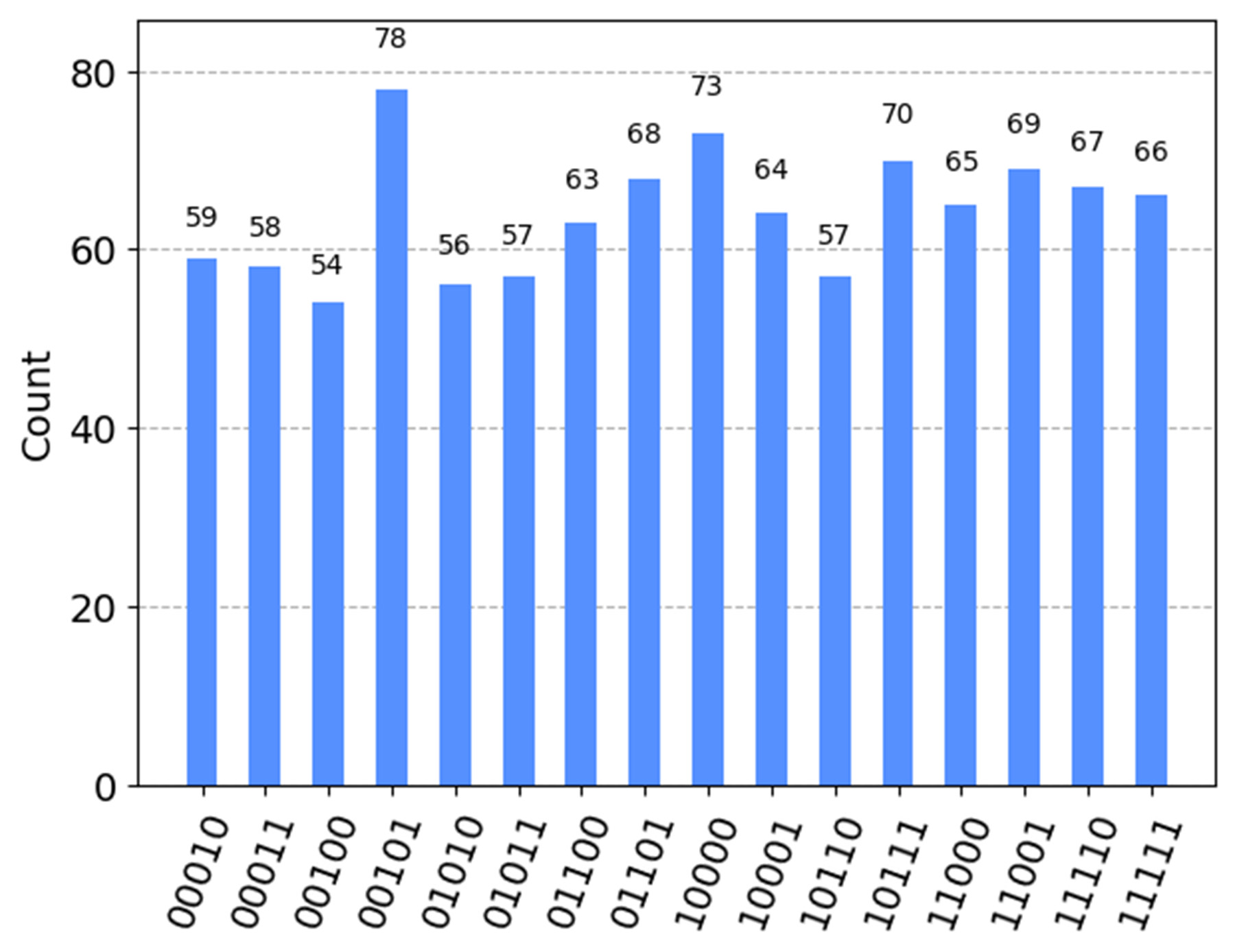
さらに100回繰り返せば、（当然のことではあるが）長大な量子回路が生成される。しかし、こうした量子回路の視覚的インパクトは、人間の知覚や素朴な直感、美しさに回収しない（真正）量子コンピュータアートの趣旨には、反しているように思える。

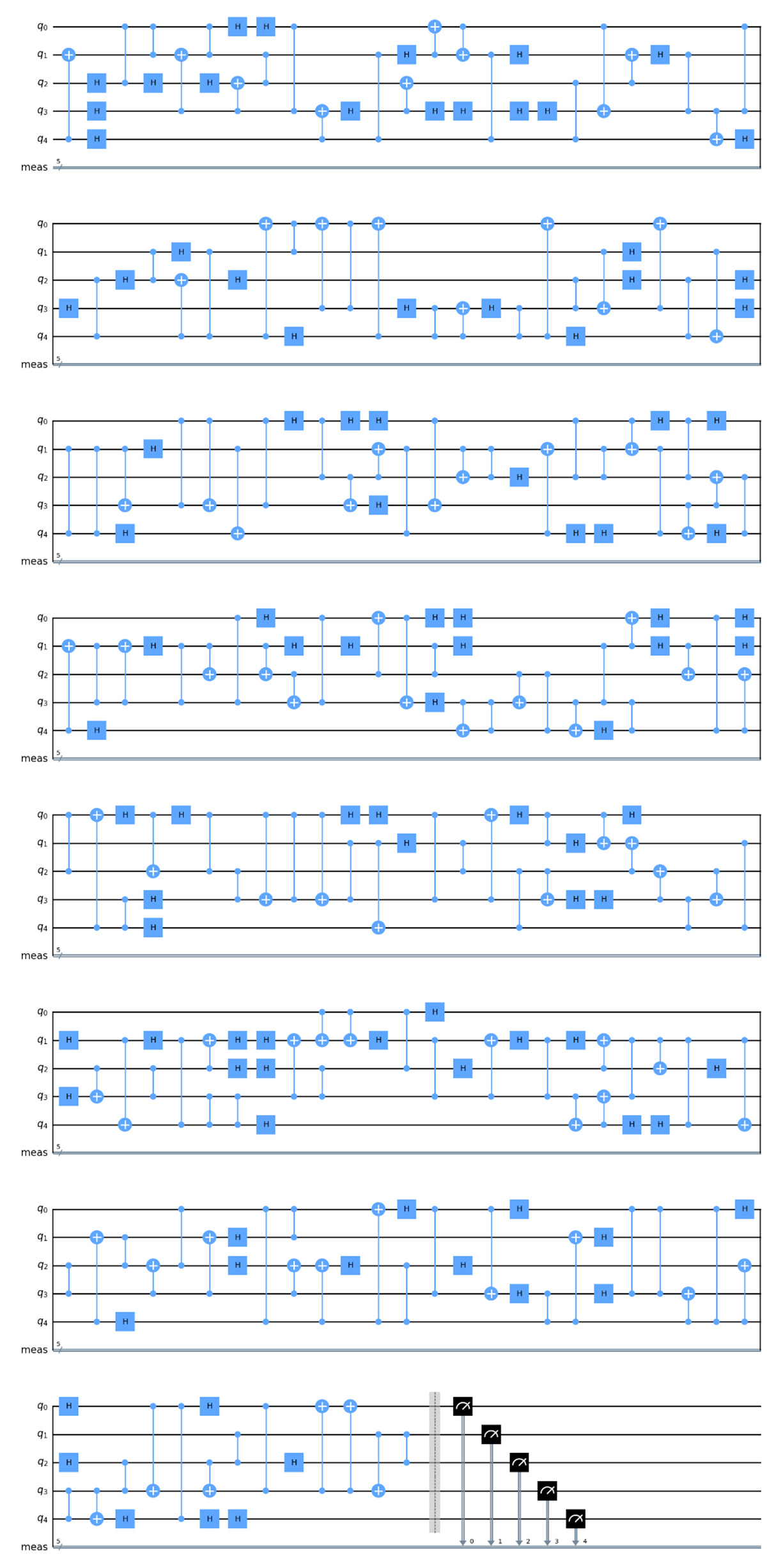
20回の繰り返しで生成されたQiskitコードを実機（ibm_lagos）で実行してみる。

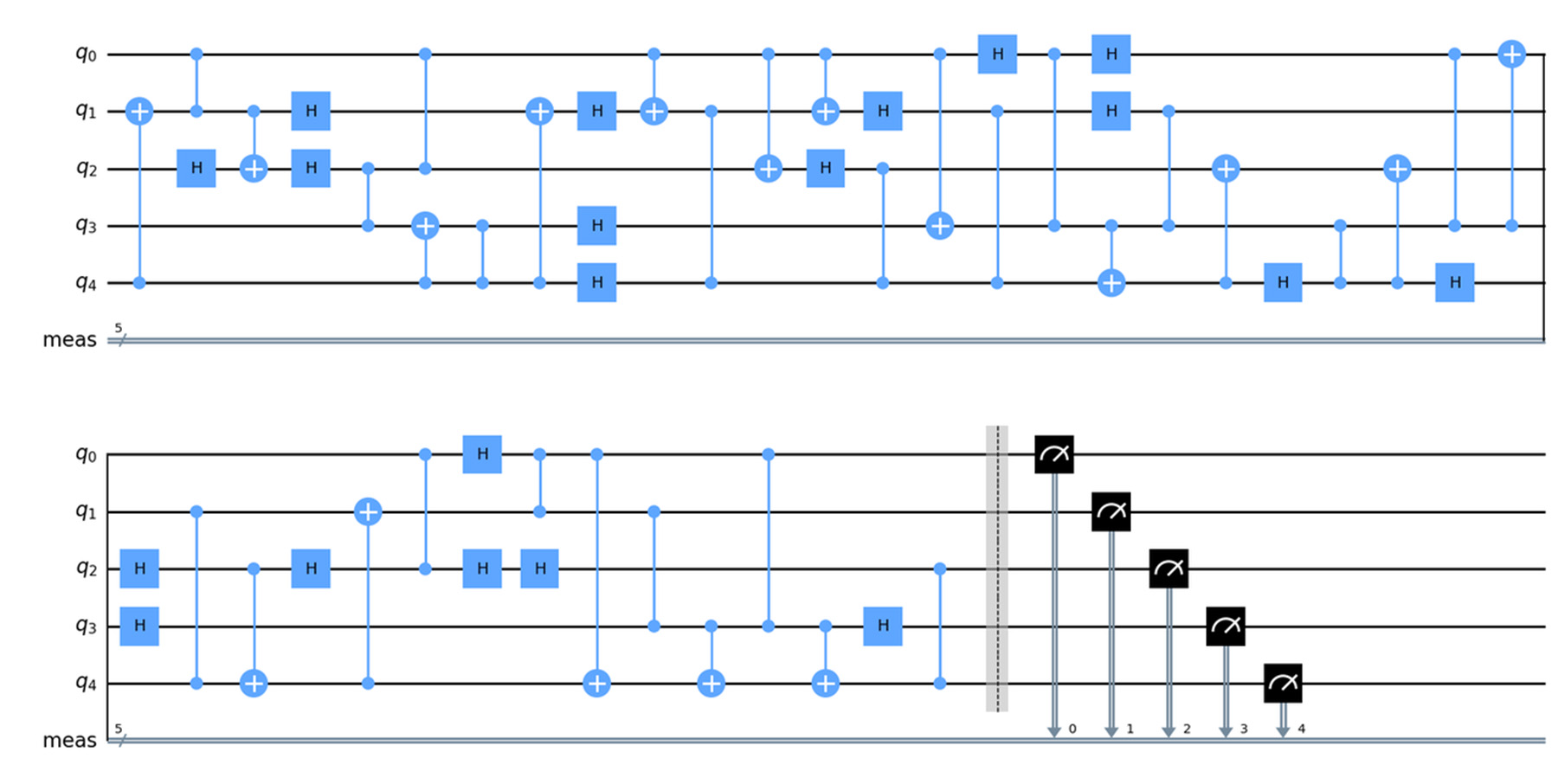
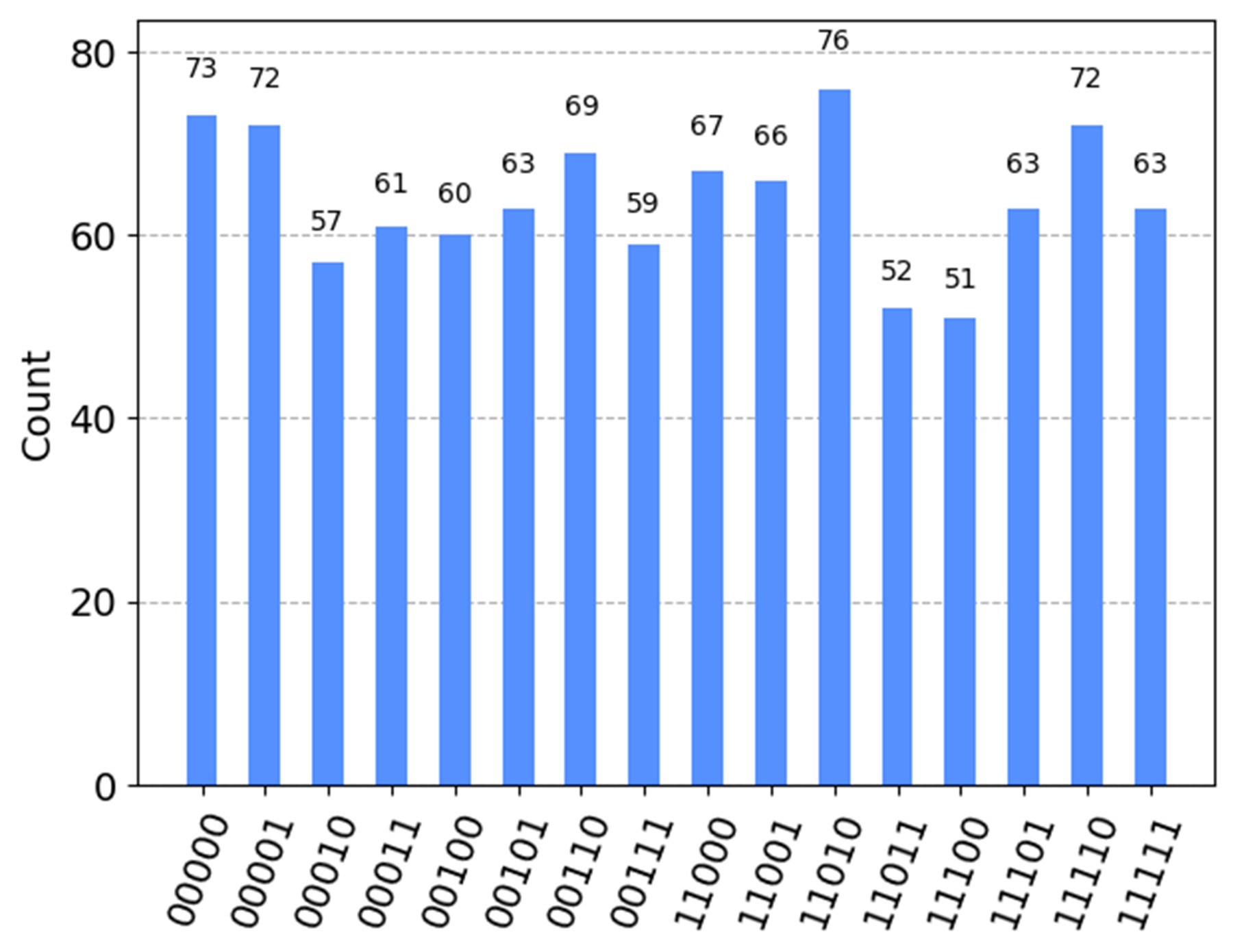
シミュレーションによる実行結果は以下の通り。

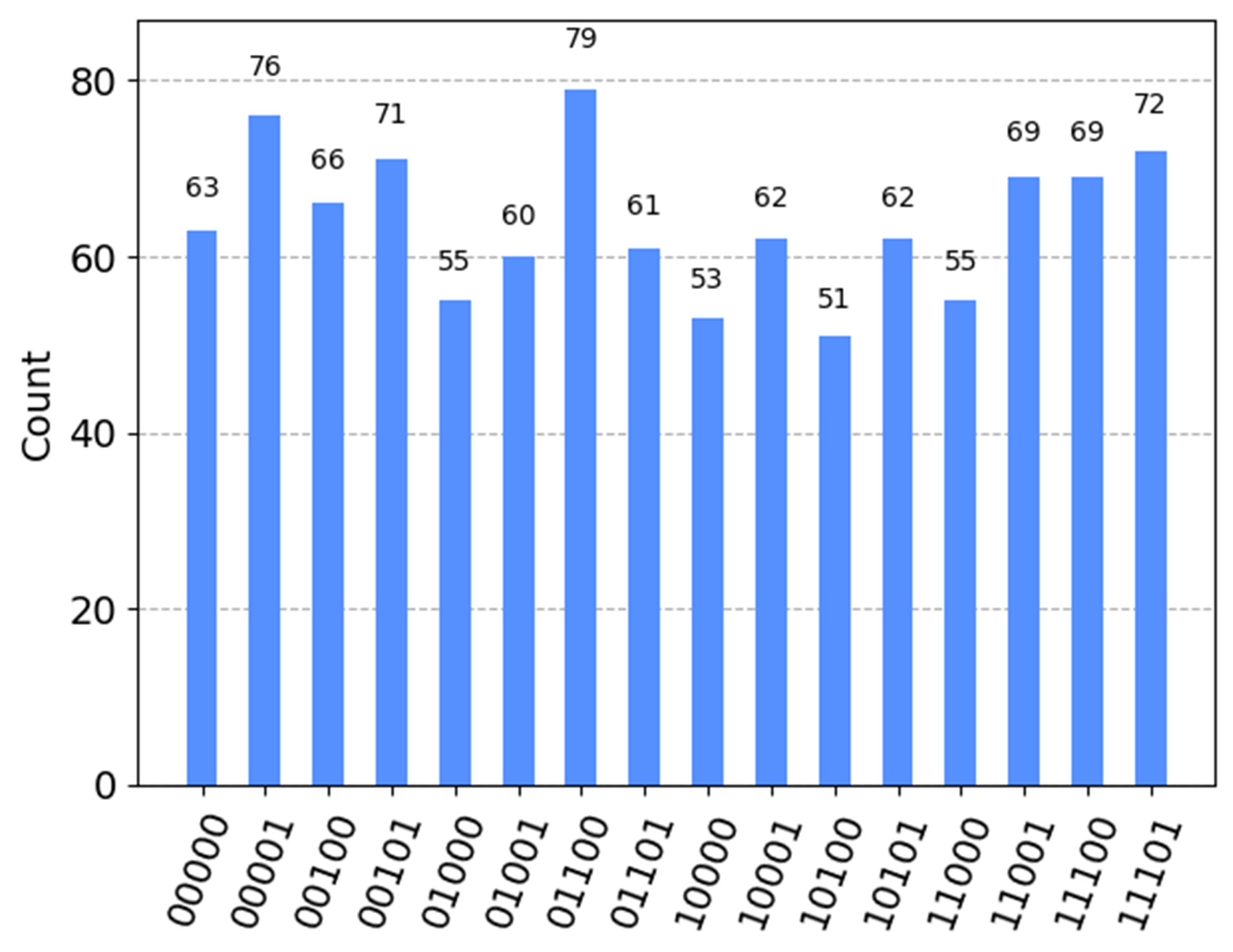
それに対して、実機による実行結果は

from qiskit import execute, IBMQ

provider = IBMQ.load_account()

backend = provider.get_backend('ibm_lagos')
job = execute(circuit, backend)
results = job.result()
print(results.get_counts(circuit))
plot_distribution(job.result().get_counts(circuit))
plot_histogram(job.result().get_counts(circuit))

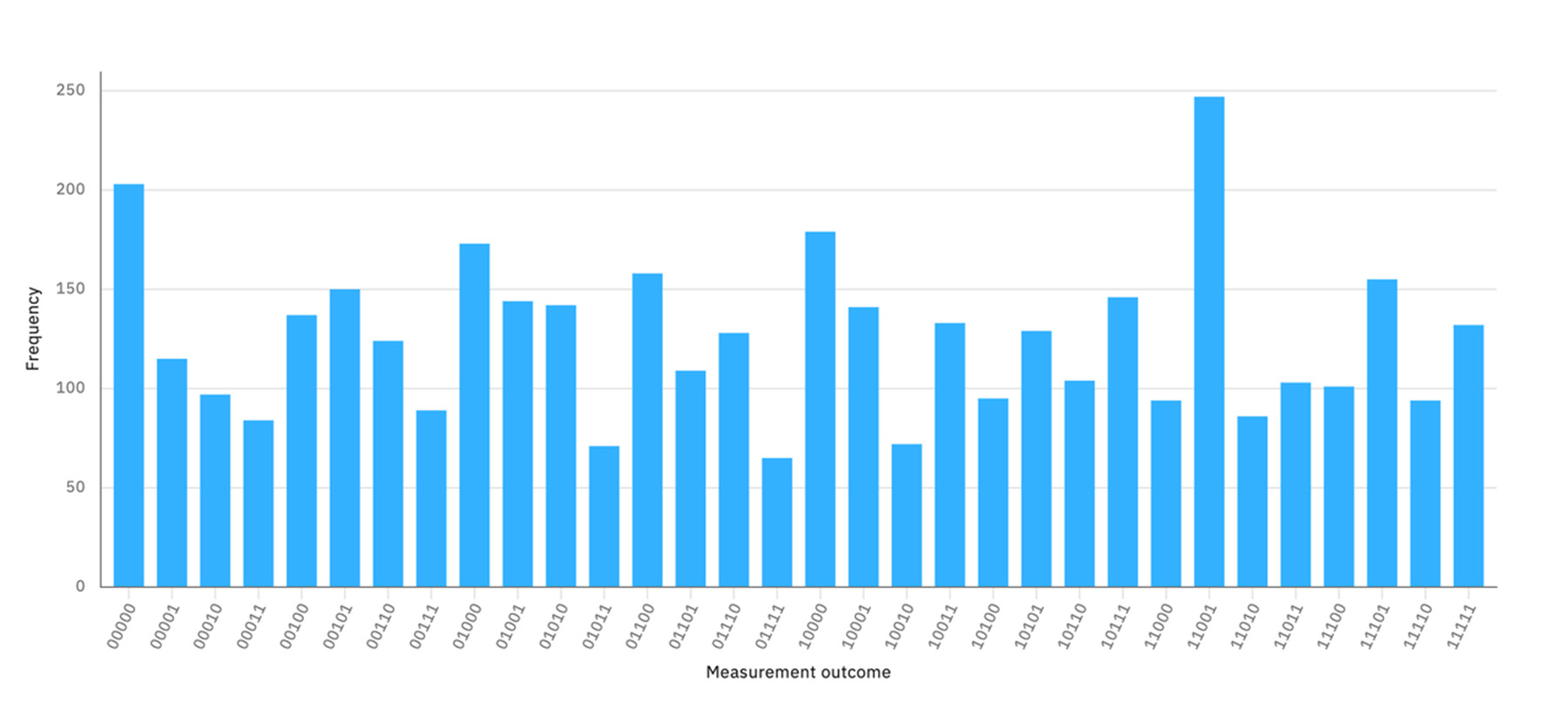
となり、実行時のエラーによって測定結果は大きくばらついている。実行した ibm_lagosのエラーマップを出力すると、アダマールゲート（H）のエラー率が平均0.046%、 CNOTゲートのエラーレートが平均1.946％であった。

from qiskit.visualization import plot_gate_map, plot_error_map, plot_circuit_layout
display(plot_error_map(backend))

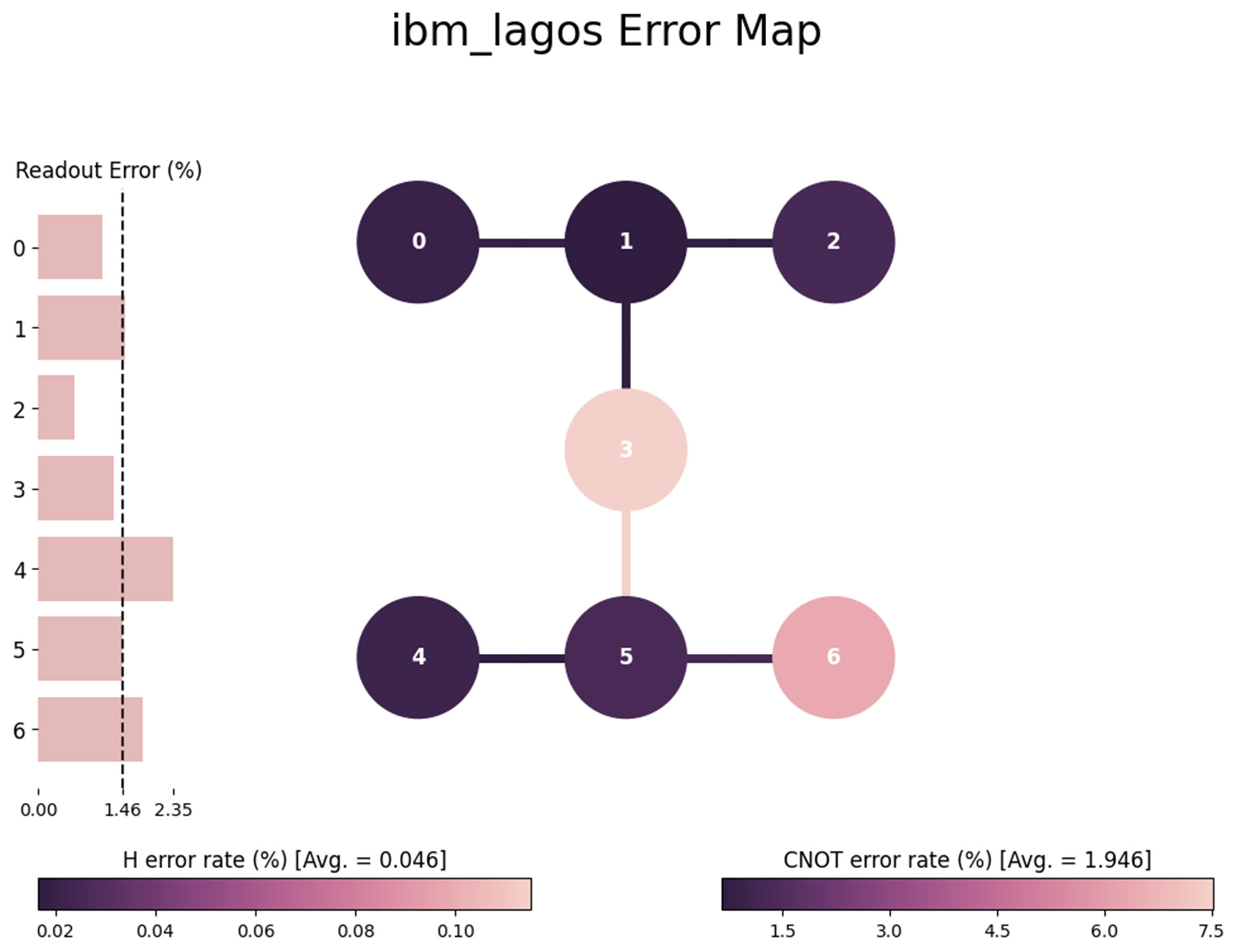
Qiskit独自のコード生成の機能として、ランダムな量子回路を直接生成することもできる。

circ = random_circuit(5, 5, measure=True)

この1行だけで、5量子ビットと5古典ビットのランダムな量子回路が生成される。

from qiskit import QuantumCircuit, Aer, transpile, assemble
from qiskit.providers.aer import AerSimulator
from qiskit.visualization import plot_histogram
from qiskit.circuit.random import random_circuit

circ = random_circuit(5, 5, measure=True)
circ.draw(output='mpl')

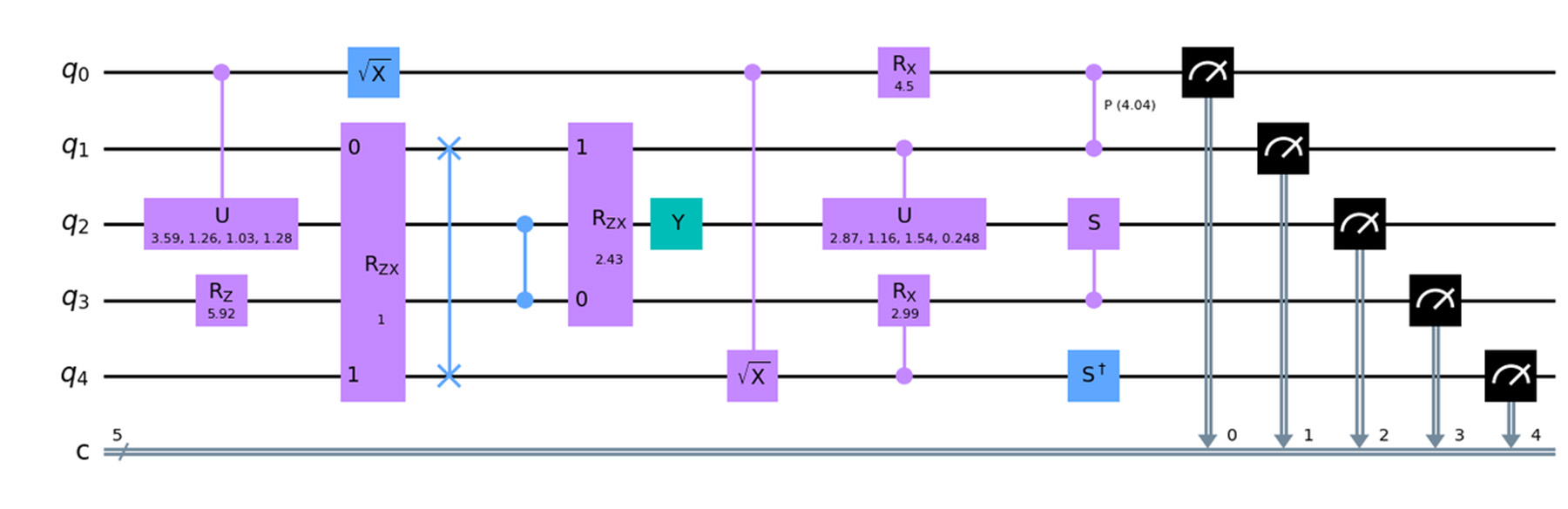
測定結果は以下のようになる。

simulator = Aer.get_backend('aer_simulator')
circ = transpile(circ, simulator)

# Run and get counts
result = simulator.run(circ).result()
counts = result.get_counts(circ)
plot_histogram(counts)

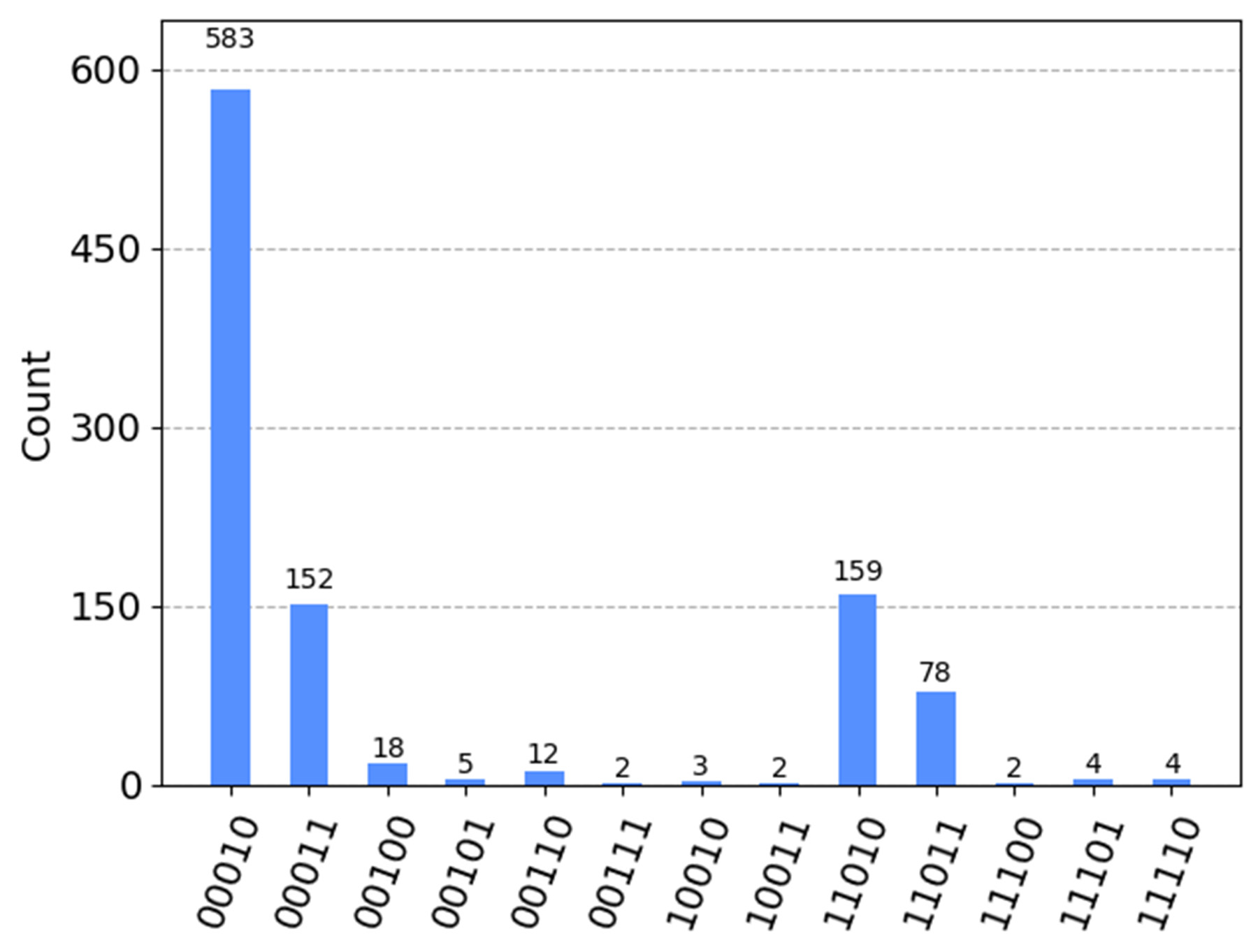
量子ビットの美的な状態

最後に、ChatGPTに以下のような問いかけをしてみた。

from qiskit import QuantumCircuit, Aer, transpile, assemble
from qiskit.visualization import plot_histogram, plot_bloch_multivector
from qiskit.providers.aer import AerSimulator

# Create a quantum circuit
qc = QuantumCircuit(5)

# Create a symmetric pattern of superposition and entanglement
qc.h(0)
qc.cx(0, 1)
qc.cx(1, 2)
qc.cx(2, 3)
qc.cx(3, 4)
qc.barrier()
qc.h([1, 3])
qc.cx(1, 2)
qc.cx(3, 4)
qc.barrier()
qc.h(2)
qc.barrier()
qc.cx(2, 3)
qc.barrier()
qc.h(2)

# Measure all qubits
qc.measure_all()

# Visualize the circuit
qc.draw('mpl')

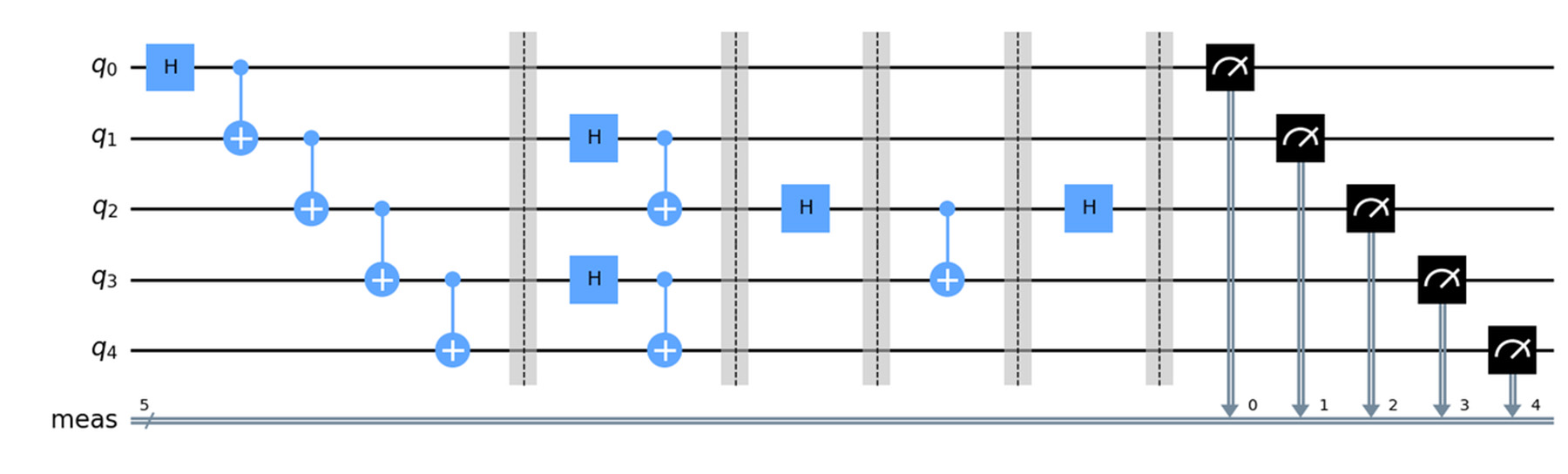
# Simulate the circuit
simulator = AerSimulator()
compiled_circuit = transpile(qc, simulator)
result = simulator.run(compiled_circuit).result()
counts = result.get_counts()
plot_histogram(counts)

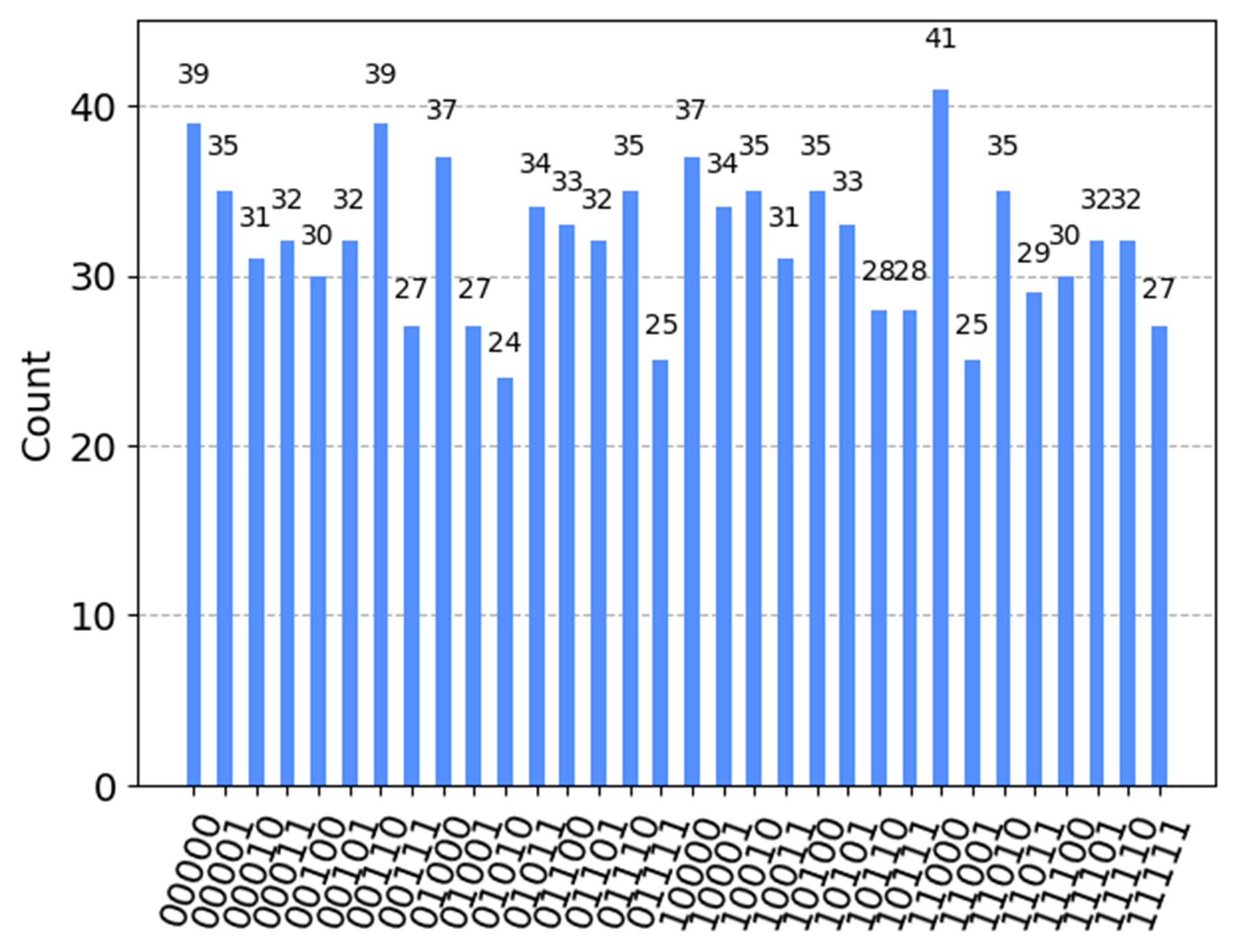
続けて、以下のような問いかけをした。

すると、以下のような答えが返ってきた。

1. 対称性：対等な重ね合わせや、ある変換のもとで不変な状態など、対称性を示す量子状態は、ある種の美的性質を持つと考えることができます。
2. もつれ合いの最大化：最大のもつれを示すベル状態やGHZ状態のような状態は、最大相関を持つという性質から特別なものと考えられます。
3. フラクタル構造：状態や回路のパターンが複数のスケールで繰り返されるフラクタル構造を示す量子状態や量子回路は、一種の美的性質や面白さを持っていると考えられます。
4. 単純さと優雅さ：最小限の操作や資源で特定の結果を達成する量子状態やアルゴリズムは、ある意味でエレガントで美しいと考えられます。
5. 調和とバランス：複数の状態の等しい重ね合わせのような、ある種のバランスを示す量子状態は、調和のとれた性質を持っていると考えられます。
6. 複雑さ：高度な複雑性や情報を持つ状態は、ある意味で興味深いもの、あるいは特別なものとみなされます。
7. 普遍性：他の状態や操作を構築するために使用できる状態や操作（量子コンピューティングにおけるユニバーサルゲートセットのような）は、ある種の生成的な美しさを持っていると考えられます。
8. 自己相似性：ある操作や変換の下で自己相似性を示す量子状態は、ある種の再帰的な美しさを持っていると考えられます。
9. 最適性：特定のタスクに最適であったり、特定のリソースを最大化するような量子状態やアルゴリズムは、特別であったりエレガントであったりすると考えられます。
10. 幾何学的な美しさ：状態空間における興味深い幾何学的構造やエレガントな幾何学的構造として可視化できる量子状態は、一種の幾何学的な美しさを持っていると考えられます。

1. 対称性：

すべての可能な状態の等しい重ね合わせ状態を作成します。

from qiskit import QuantumCircuit, Aer, transpile, assemble
from qiskit.visualization import plot_histogram

# Create a quantum circuit
qc = QuantumCircuit(3)

# Apply Hadamard gates to create equal superposition
qc.h([0, 1, 2])

# Measure all qubits
qc.measure_all()

# Visualize the circuit
qc.draw('mpl')

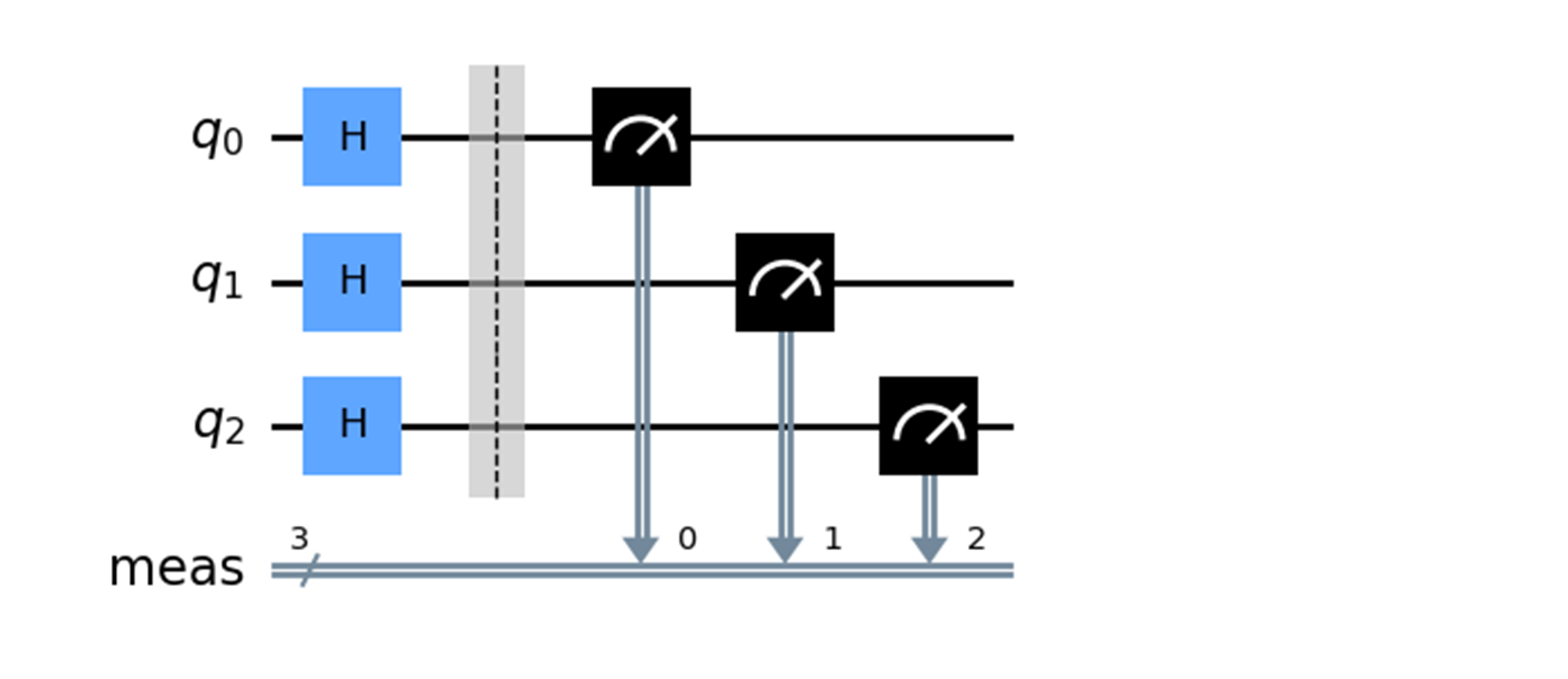
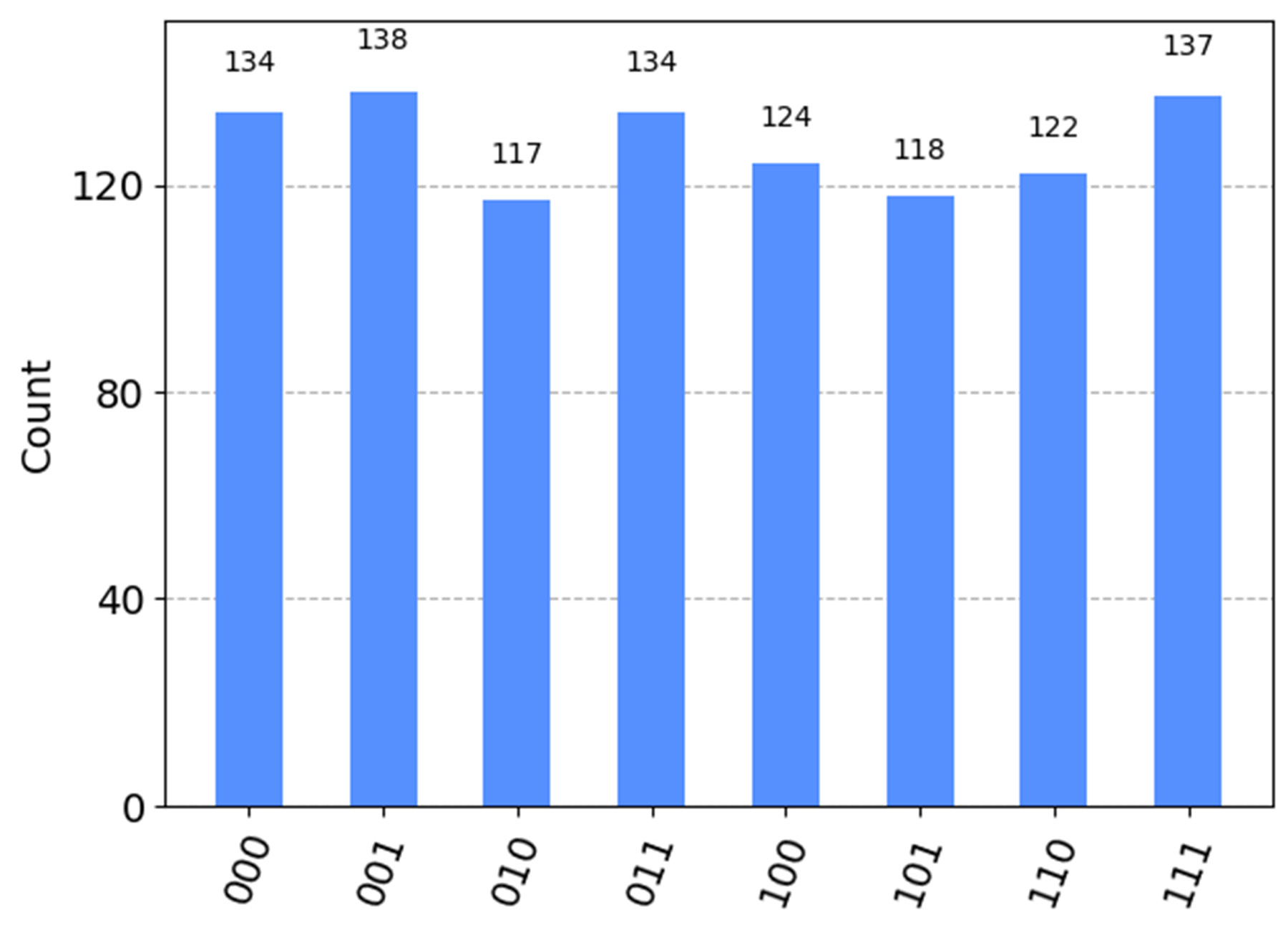
2. もつれ合いの最大化：

Greenberger-Horne-Zeilinger(GHZ)状態を作ります。

# Create a quantum circuit
qc = QuantumCircuit(3)

# Create a GHZ state
qc.h(0)
qc.cx(0, 1)
qc.cx(0, 2)
 
# Measure all qubits
qc.measure_all()

# Visualize the circuit
qc.draw('mpl')

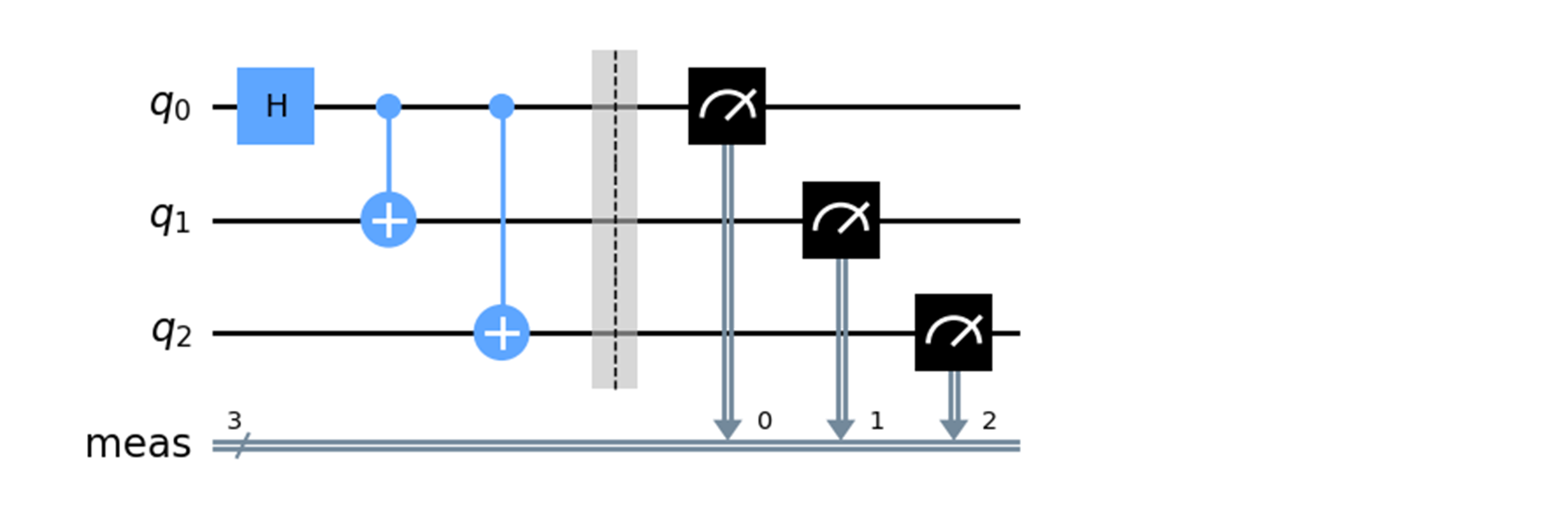
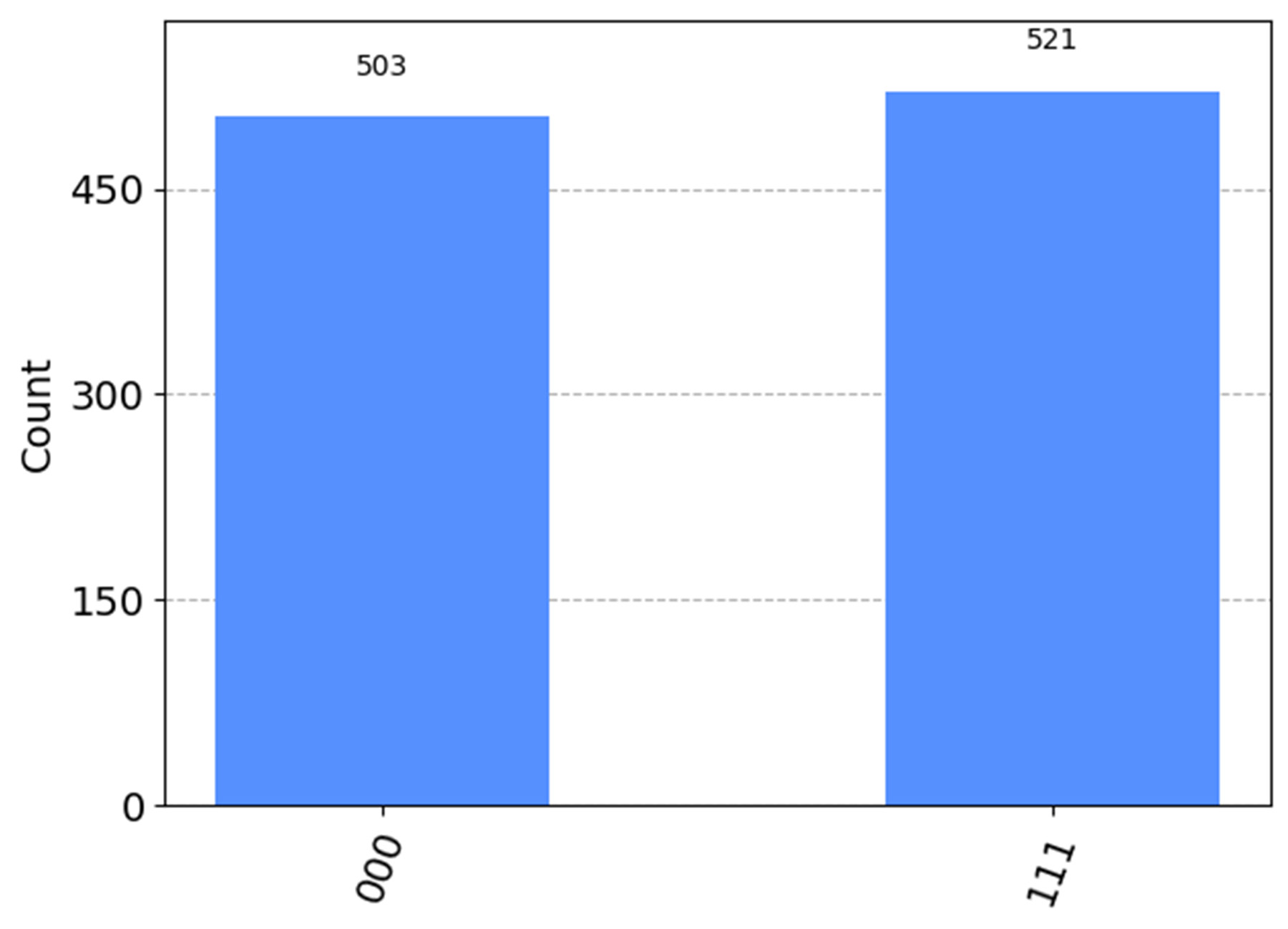
3. フラクタル構造：

一種のフラクタル構造を形成する、ゲートの繰り返しパターンを持つ回路を作成します。

# Create a quantum circuit
qc = QuantumCircuit(3)

# Repeated pattern of gates
for _ in range(3):
    qc.h([0, 1, 2])
    qc.cx(0, 1)
    qc.cx(1, 2)
    qc.barrier()

# Measure all qubits
qc.measure_all()

# Visualize the circuit
qc.draw('mpl')

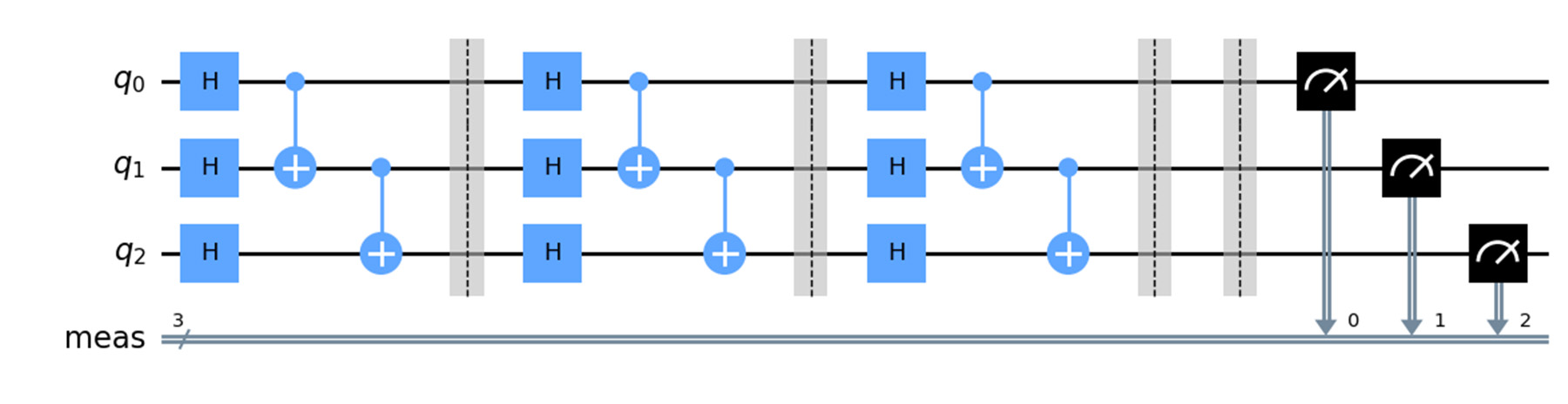
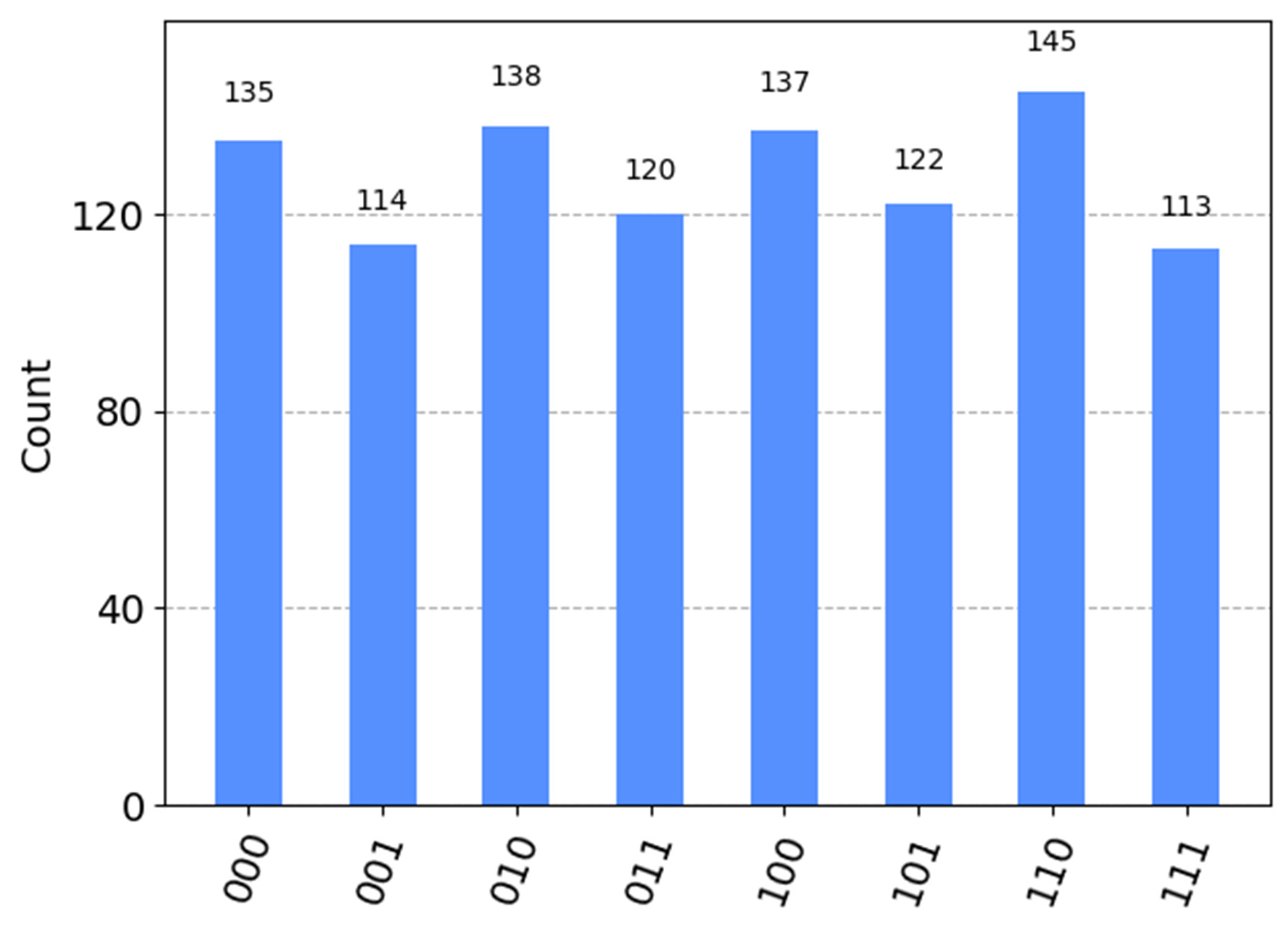
4. 単純さと優雅さ：

最小限のリソースで量子テレポーテーションを実装します。

# Create a quantum circuit
qc = QuantumCircuit(3, 1)

# Create initial state to teleport
qc.x(0)
qc.barrier()

# Create Bell pair
qc.h(1)
qc.cx(1, 2)
qc.barrier()

# Perform teleportation
qc.cx(0, 1)
qc.h(0)
qc.measure(0, 0)
qc.cx(1, 2)
qc.cz(0, 2)

# Visualize the circuit
qc.draw('mpl')

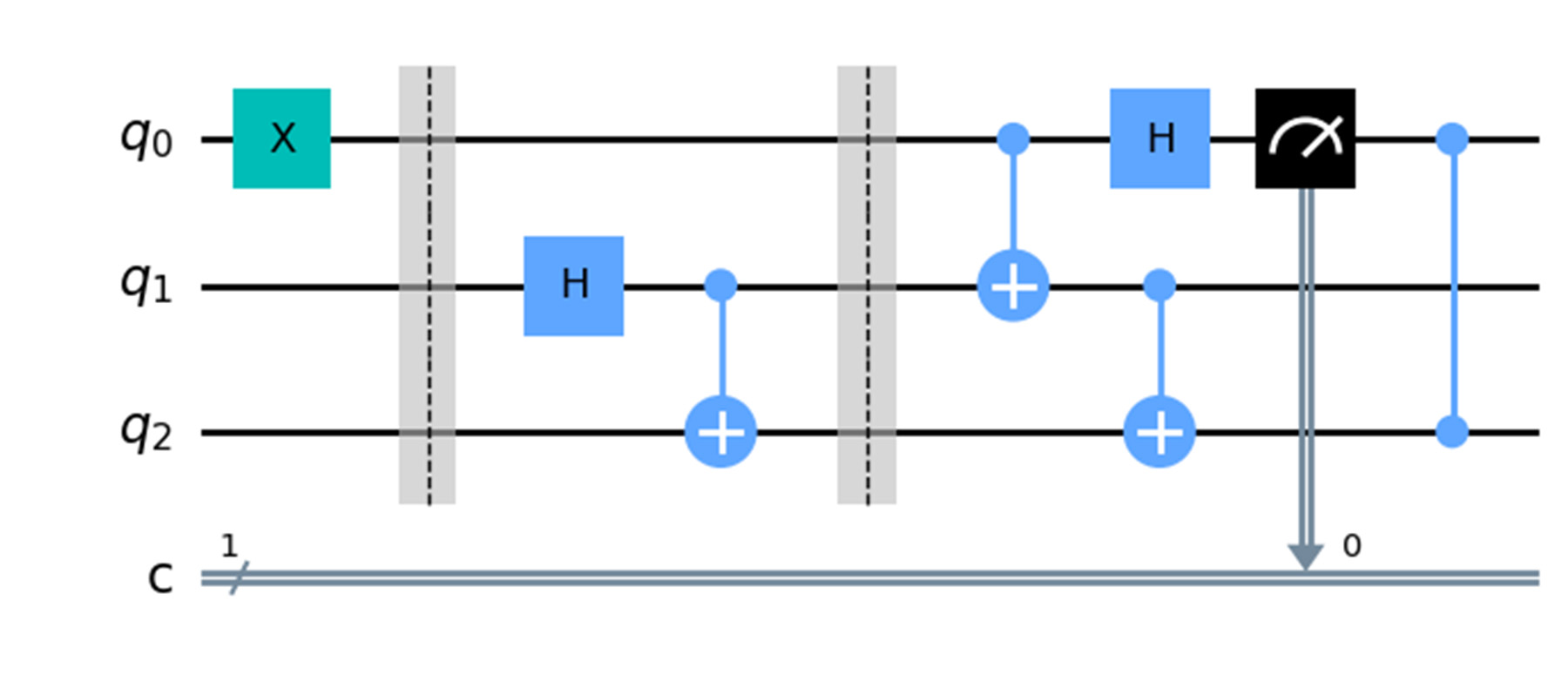
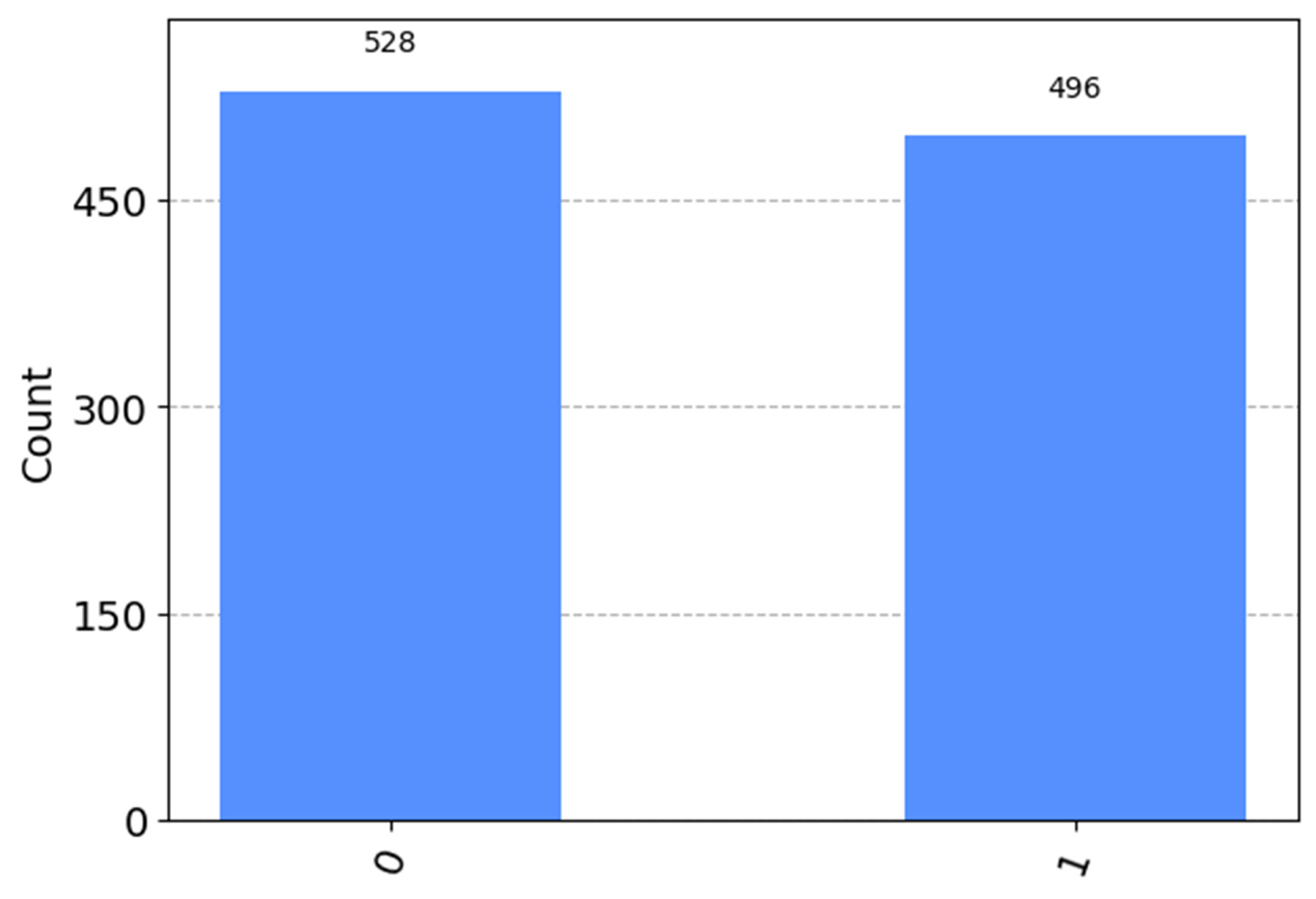
この量子回路は量子テレポーテーションの基本原理を示していて、q[0]の状態を、もつれたペア（q[1]とq[2]）を使ってq[2]にテレポートしようとしています。

5. 調和とバランス：

別のゲートを交互に並べた回路を作ります。

# Create a quantum circuit
qc = QuantumCircuit(3)

# Alternating pattern of gates
for _ in range(3):
    qc.h([0, 1, 2])
    qc.barrier()
    qc.cx(0, 1)
    qc.cz(1, 2)
    qc.barrier()

# Measure all qubits
qc.measure_all()

# Visualize the circuit

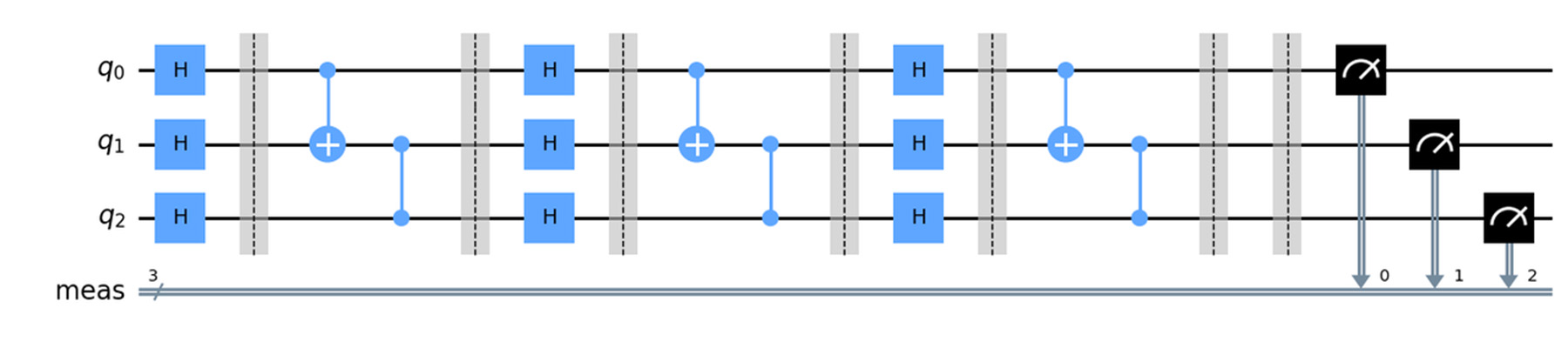
これは、「フラクタル構造」のコードのCNOTゲートの一部を、SWAPゲートに置き換えたものになっている。

測定と演算のインタラクション

こうした例を見ていると、測定と演算の関係が再び気になったので、もう一度質問してみた。

ポスト・セレクション：

この例では、もつれた状態を準備し、その後測定を行う回路を作ります。一方の量子ビットの測定結果に応じて、もう一方の量子ビットの状態が影響を受けます。

from qiskit import QuantumCircuit, Aer, transpile, assemble
from qiskit.visualization import plot_histogram, plot_bloch_multivector
from qiskit.providers.aer import AerSimulator

# Create a quantum circuit
qc = QuantumCircuit(2, 2)

# Prepare an entangled state
qc.h(0)
qc.cx(0, 1)

# Measure qubit 0
qc.measure(0, 0)

# Depending on the result, apply X gate to qubit 1
qc.x(1).c_if(qc.clbits[0], 1)

# Measure qubit 1
qc.measure(1, 1)

# Visualize the circuit
qc.draw('mpl')

# Simulate the circuit
simulator = AerSimulator()
compiled_circuit = transpile(qc, simulator)
result = simulator.run(compiled_circuit).result()
counts = result.get_counts()
plot_histogram(counts)

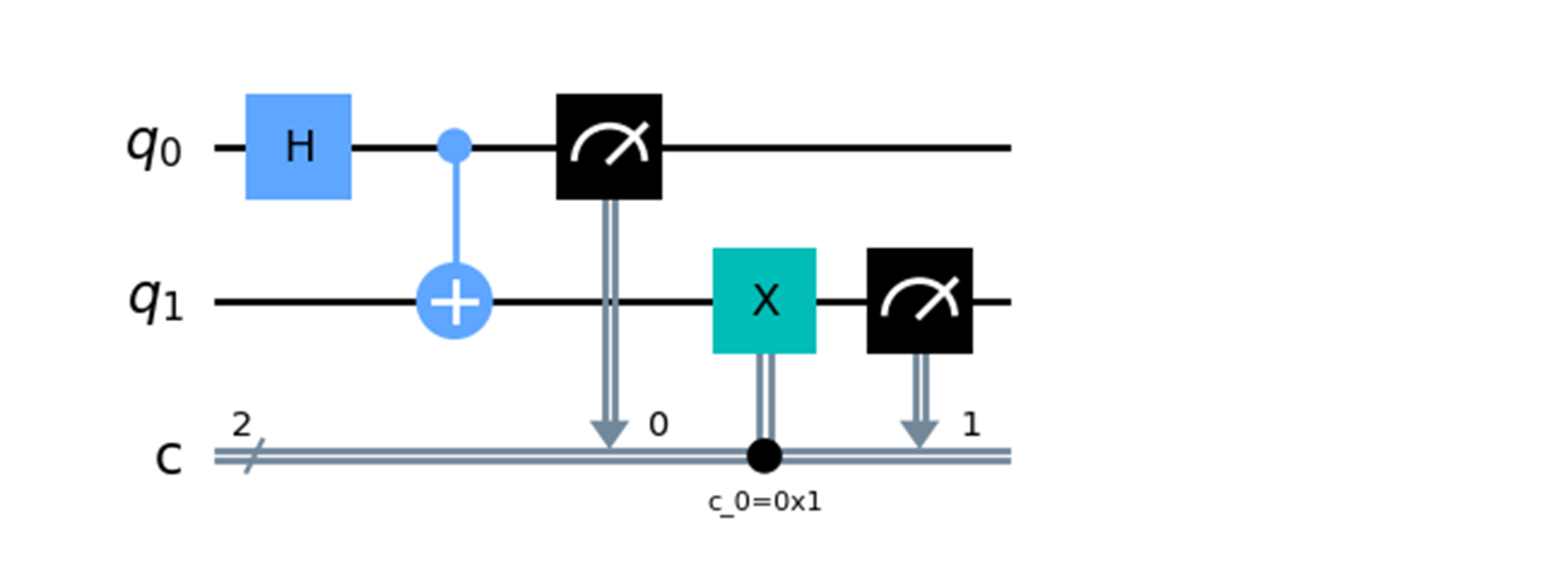
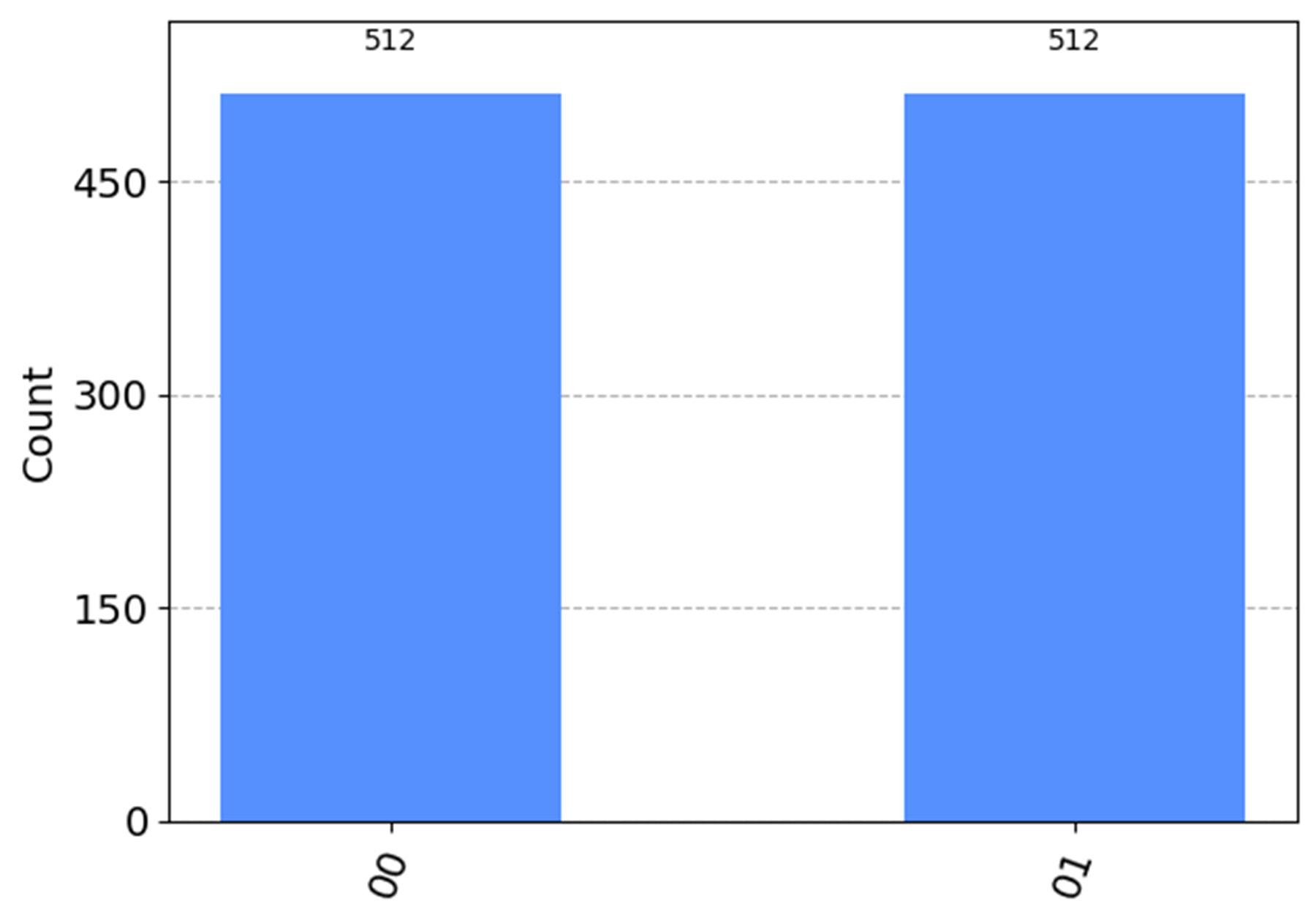
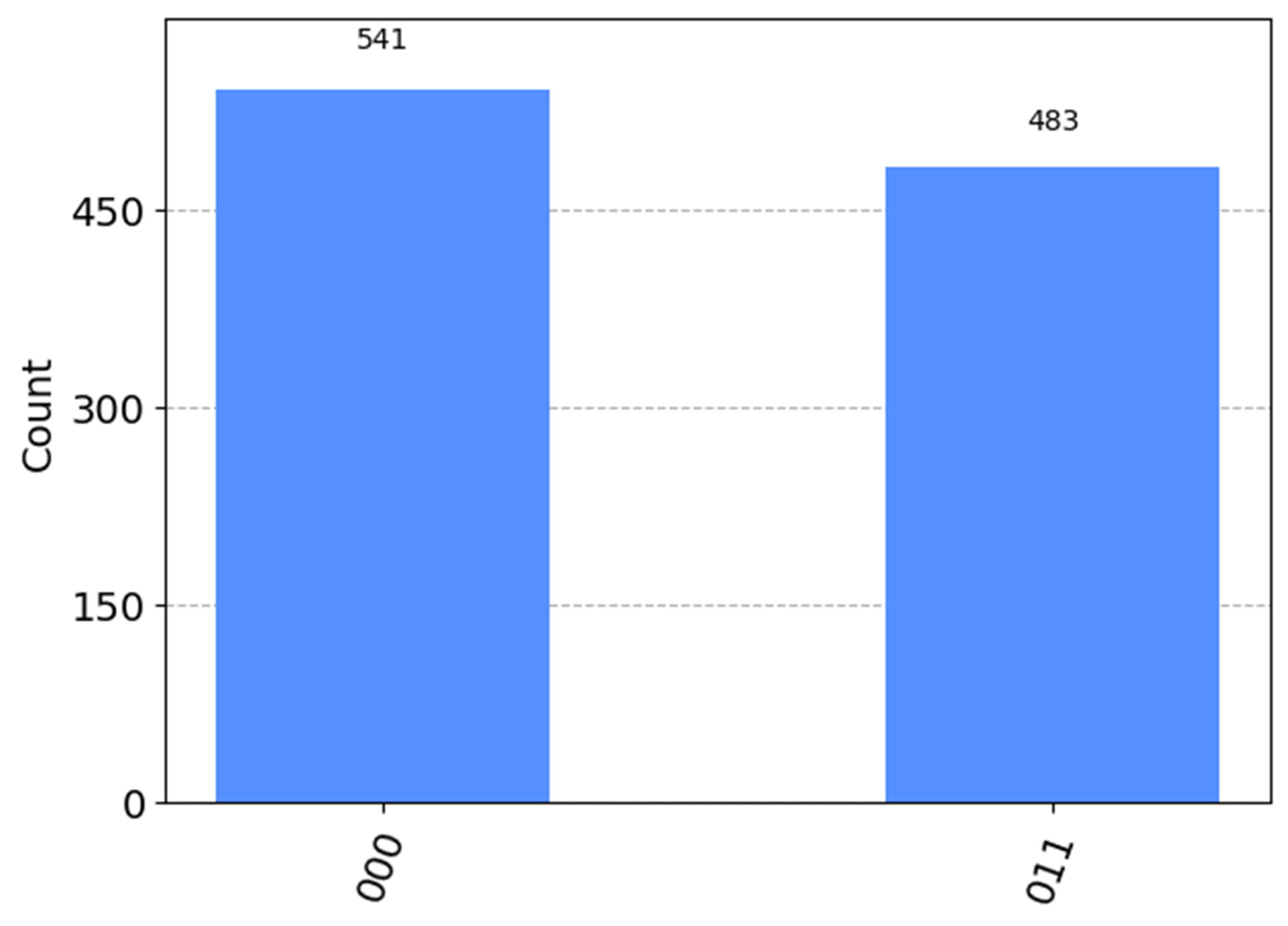
q[0]の測定結果が0であれば、エンタングルしているq[1]も0になり、そのときはq[1]は変化しない。q[0]が1であれば、q[1]も1になり、その場合はq[1]を反転させる。いずれにしても、q[1]は常に0になる。せっかくなので、もう少し他の例を挙げてもらうことにする。

条件演算とフィードバック：

この例では、3つの量子ビットを持つ回路を作成し、一連の演算と測定を行います。この場合、後続の演算は以前の測定結果を条件とし、回路内に一種のフィードバックループを作成します。

from qiskit import QuantumCircuit, Aer, transpile, assemble
from qiskit.visualization import plot_histogram
from qiskit.providers.aer import AerSimulator

# Create a quantum circuit
qc = QuantumCircuit(3, 3)

# Prepare a superposition on qubit 0
qc.h(0)

# Entangle qubits 0 and 1
qc.cx(0, 1)

# Create a superposition on qubit 2
qc.h(2)

# Measure qubit 0
qc.measure(0, 0)

# Conditionally apply X gate on qubit 1 based on measurement of qubit 0
qc.x(1).c_if(qc.clbits[0], 1)

# Measure qubit 1
qc.measure(1, 1)

# Conditionally apply Z gate on qubit 2 based on measurement of qubit 1
qc.z(2).c_if(qc.clbits[1], 1)

# Measure qubit 2
qc.measure(2, 2)

# Visualize the circuit
qc.draw('mpl')

# Simulate the circuit
simulator = AerSimulator()
compiled_circuit = transpile(qc, simulator)
result = simulator.run(compiled_circuit).result()
counts = result.get_counts()
plot_histogram(counts)

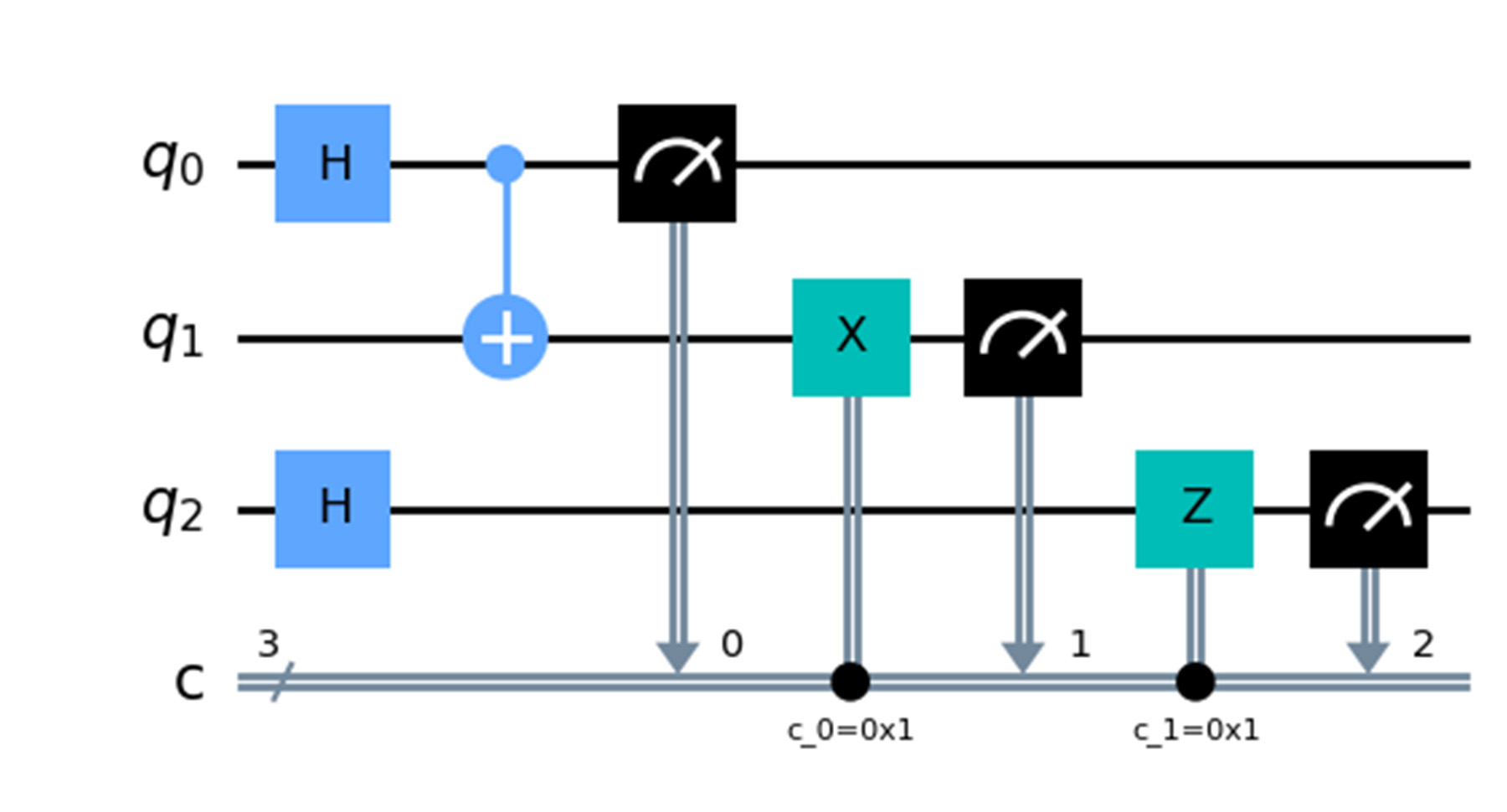
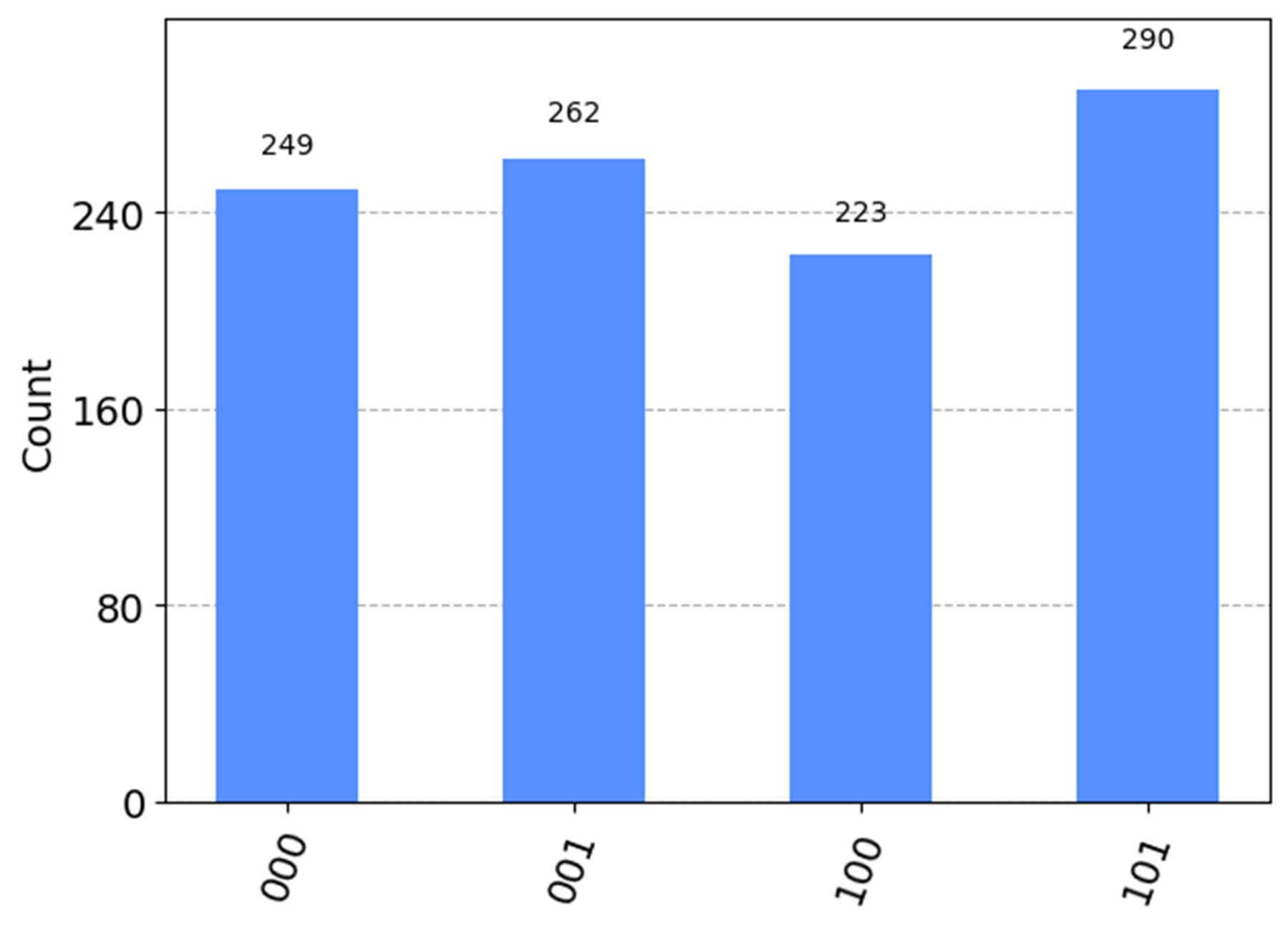
これは、先ほどの例に加えて、重ね合わせの状態にある第3の量子ビットq[2]が、q[1]の状態によって変化する。ただしq[1]は常に0なので、Zゲートは適用されず、q[2]の測定結果には、0と1が等しく現れる。ただし、Zゲートは位相反転ゲートなので、適用されても測定結果の確率分布に変化はない。

条件演算とエンタングルメントによる複雑な量子回路：

この例では、4つの量子ビットを持つ回路を作成し、一連の演算と測定を行います。後続の演算は、以前の測定結果を条件とするため、回路内に複雑なダイナミクスが生まれます。

from qiskit import QuantumCircuit, Aer, transpile, assemble
from qiskit.visualization import plot_histogram
from qiskit.providers.aer import AerSimulator

# Create a quantum circuit
qc = QuantumCircuit(4, 4)

# Prepare a superposition on qubit 0 and qubit 2
qc.h([0, 2])

# Entangle qubits 0 and 1
qc.cx(0, 1)

# Entangle qubits 2 and 3
qc.cx(2, 3)

# Measure qubit 0
qc.measure(0, 0)

# Conditionally apply X gate on qubit 1 based on measurement of qubit 0
qc.x(1).c_if(qc.clbits[0], 1)

# Apply a Hadamard gate to qubit 1 and qubit 3
qc.h([1, 3])

# Measure qubit 2
qc.measure(2, 2)

# Conditionally apply Z gate on qubit 3 based on measurement of qubit 2
qc.z(3).c_if(qc.clbits[2], 1)

# Entangle qubits 1 and 3
qc.cx(1, 3)

# Measure qubit 1
qc.measure(1, 1)

# Conditionally apply X gate on qubit 3 based on measurement of qubit 1
qc.x(3).c_if(qc.clbits[1], 1)

# Measure qubit 3
qc.measure(3, 3)

# Visualize the circuit
qc.draw('mpl')

# Simulate the circuit
simulator = AerSimulator()
compiled_circuit = transpile(qc, simulator)
result = simulator.run(compiled_circuit).result()
counts = result.get_counts()
plot_histogram(counts)

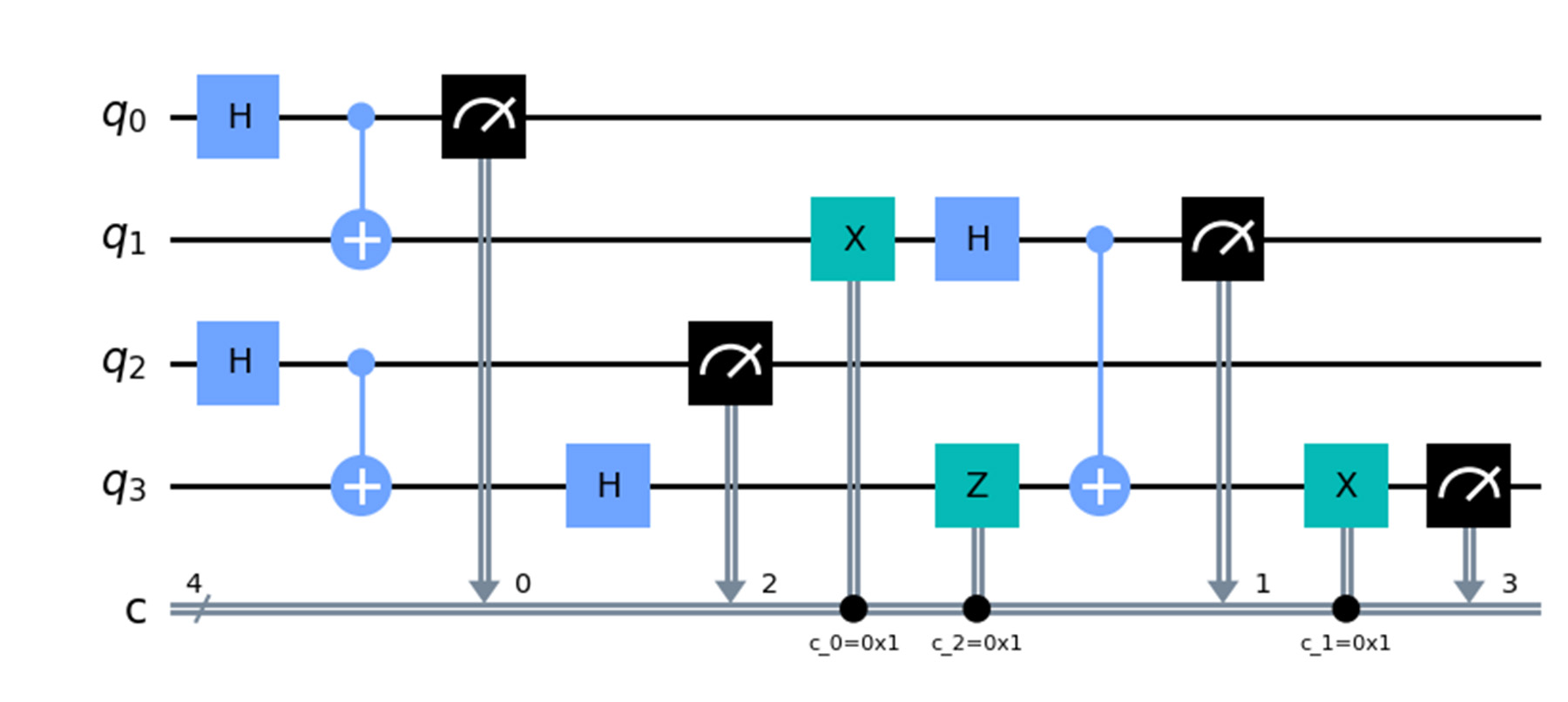
この回路はq[0]とq[1]、q[2]とq[3]がもつれ合った状態から出発する。q[0]の測定結果によってq[1]にXゲートを適用するかが決まる。q[2]の測定結果によって、q[3]にZゲートを適用するかどうかが決まる。q[0]もq[2]も測定結果が0と1になる確率は等しい。q[2]の測定によって、q[3]の値も0か1のどちらかになるが、q[1]とq[3]にアダマールゲートが適用されて、重ね合わせの状態になっているので、Zゲート、CNOTゲート、あるいはXゲートの適用の有無にかかわらず、測定結果には0と1が等しく現れる。最終的には、0000から1111までが（ほぼ）等しく現れる。

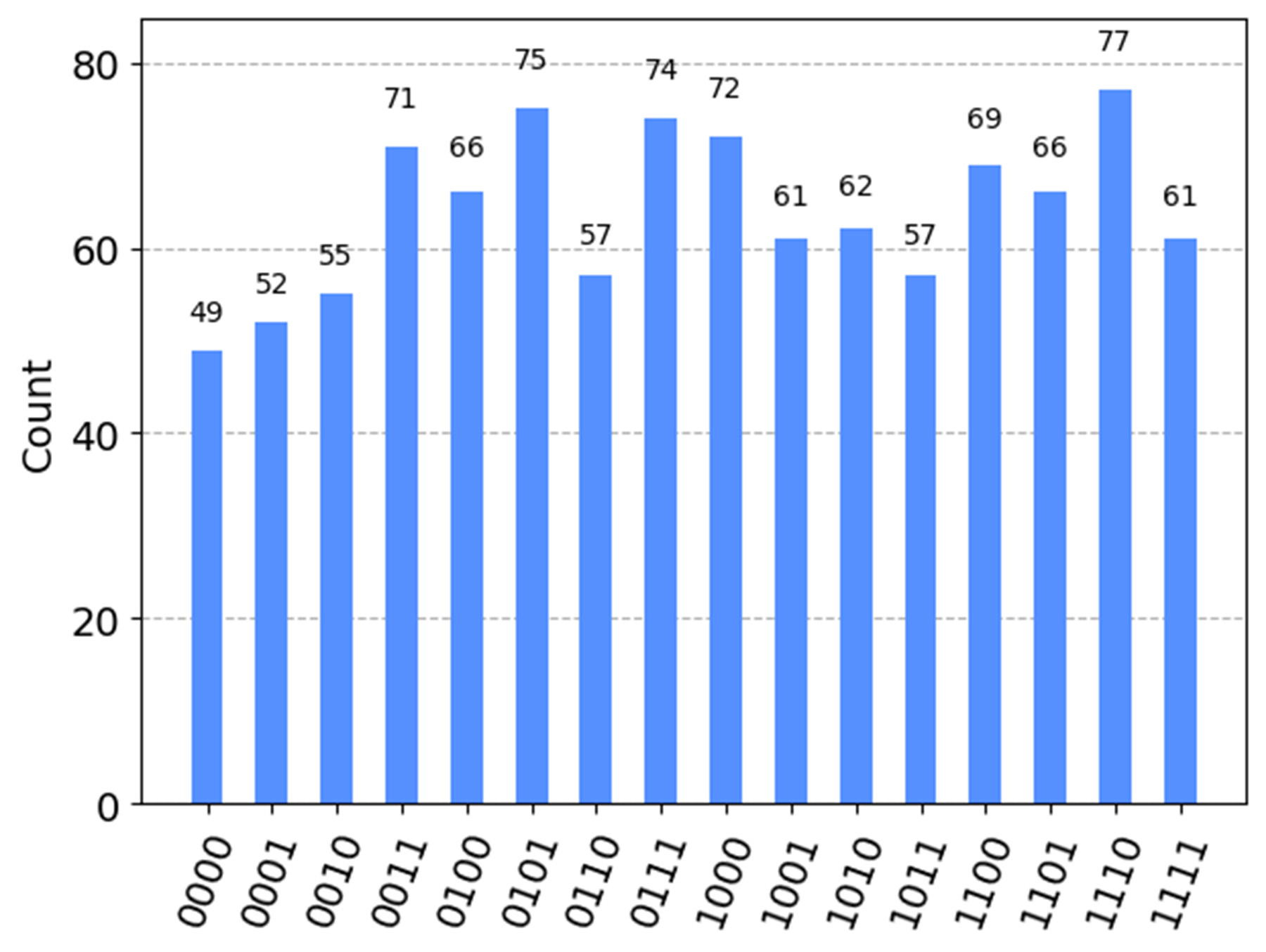
（つづく）

参考：以上のQiskitコードと実行結果は、Jupyter notebookファイル^※10にまとめられている。