タイポグラフィとしてのスタイルシート
タイポグラフィでは、文字や単語は機械的な手法で生み出されます。……（サイズや位置などの）情報は他の人に渡すことができ、別の機会にまったく同じものを再現することもできます。
フレット・スメイヤーズ『カウンターパンチ※1』
タイポグラフィとは、人の手によって直接描かれるものではなく、機械的な手法によって生成されるものです。そして、その書体や文字サイズや行間といったものをデータとして定義でき、そのデータをもとにまったく同じものを再現できるものでもあります。
ここに示したのはウェブサイトやモバイルアプリケーションなどの表示スタイルを記述する言語であるCSS（カスケーディング・スタイル・シート）のコードです。これによって書体や文字サイズ、行間、そして文字サイズを基準にしたスペーシングなどが定義されます。このコードをもとにして、ウェブブラウザなどユーザーエージェントという機械が文字を整形して表示する。これは表示する環境が変わっても再現可能です。タイポグラフィの定義を見れば、こういったCSSのコード片も、タイポグラフィであることがわかります。
紙面に文字を配置する技術として数百年の歴史を持つタイポグラフィですが、近年はパソコンやスマートフォンなどデジタルデバイスの画面にもその領域を広げてきました。本稿ではウェブサイトやアプリケーションなどのオンスクリーンメディアにおける実践を題材にして、タイポグラフィを考察していきます。
音楽と数学から考えるタイポグラフィ
欧米のタイポグラフィの本を読んでいると、必ずと言っていいほど出くわすのが音楽の話です。しかも「リズムを意識しましょう」とか「ハーモニーが大切です」とかいった抽象論や精神論ではなく、 数学に基づいた音楽理論をもとにタイポグラフィを解説している例が多々あるのです。
Robert Bringhurst “The Elements of Typographic Style※2”
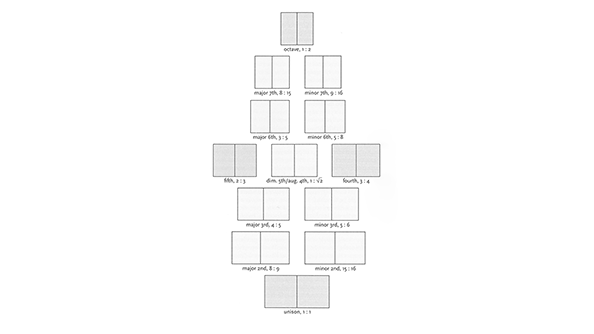
この図版はカナダの詩人でありタイポグラファーのロバート・ブリングハーストが書いた『The Elements of Typographic Style』という本に掲載されているもの。それぞれ本の見開きの状態が示されていて、ページの縦横比をいかにデザインするかということが語られています。いちばん上は縦長の本でページの縦横比が1 : 2。いちばん下は正方形の本で比率は1 : 1。さらにその間に様々な縦横比のバリエーションがあり、これらのページの比率はすべて音楽における音程の周波数比になっているのです。
音の高さは周波数によって決まります。ここでは基準となる音と各音程との周波数の比率を示しています。ユニゾン、つまりまったく同じ高さの2音の周波数比は1 : 1で、オクターブ上の音は1 : 2になります。こういった音程の周波数比をページの寸法に適用しているわけです。
またこれらの数字を見ていくと、わたしたちに馴染みの深い比率が多く含まれています。たとえば画像や映像のアスペクト比でよく使われる、短7度の16 : 9や完全5度の3 : 2、完全4度の4 : 3といった比率があります。また短6度の5 : 8は黄金比に近く、減5度（増4度）の1 : √2は白銀比です。
音楽と諸芸術は、数学の姉妹である。全ての芸術と同じように、音楽もまた自然の法則に基づいている。
ヨゼフ・ミューラー゠ブロックマン『グリッドシステム ― グラフィックデザインのために※3』
タイポグラフィに数学的思考を取り入れモダンデザインを牽引したヨゼフ・ミューラー゠ブロックマンが言うように、デザインと音楽には深い関連性がある。つまり、タイポグラフィの背後には必ず数学的なロジックが潜んでいます。当然、最終的にはデザイナーの「眼」で見て判断されるわけですが、その前に音楽や数学のロジックはガイドラインとして大いに力を発揮するのです。
音楽には様々な要素が複雑に関係しており、そのコアになるのはハーモニー、リズム、メロディという3つであると言われています。「ハーモニー」は、複数の音の調和のこと。ギターやピアノで弾くコードや、オーケストラなどでたくさんの音が同時に鳴ったり、アカペラで声がハモったりといったものを想像してください。「リズム」というのは、音楽の時間的な変化。もっともわかりやすいのはドラムやメトロノームなどの拍。「メロディ」は、旋律とも言いますが、たとえばロックバンドのヴォーカルやジャズのピアノソロなどで表現されるものです。
この音楽の3要素に沿って、それぞれがタイポグラフィにどう関係するのか、またその背後にどのような数学的ロジックがあるのかを見ていきたいと思います。
ハーモニー
「ハーモニー」とは音が協和すること、つまりいくつかの音が合わさって心地よい響きを生むことを言います。日本語で「調和」とも訳されます。音の高さは振動数によって決まるという話をしましたが、音が調和するということはつまり、振動数の比率がちょうどいいバランスになっている状態です。
タイポグラフィにおける調和とは何かというと、文字サイズや行間、グリッドのカラム幅など、様々なサイズが美しい比率で画面上に共存している状態です。今回はその中でも、文字サイズの調和について考えてみます。
オンスクリーンメディアでは、本文、見出し、キャプション、ボタンといった様々な文字サイズのテキストが要素となって画面が構成されます。そこでは、たとえば見出しを本文よりどのくらい大きくするか、またキャプションをどのくらい小さくするかといった選択によって、画面の調和が決まってくるのです。このときに、それぞれの文字サイズを場当たり的に決めるのではなく、あらかじめ一連のサイズを用意して組み合わせながら画面を構成します。ここで用意される一連のサイズを「スケール」と言います。
文字サイズのスケールは、音楽におけるスケール、つまり音階に当たります。このスケールを無視して適当に弾いていたら、調子外れな演奏になってしまうので、曲に調和するスケールに沿って演奏するわけです。これは文字サイズも同様です。ボタンの文字サイズがコンポーネントによってバラバラだと、調和が得られません。タイポグラフィ設計は、まず文字サイズのスケールを定義するところから始める必要があります。
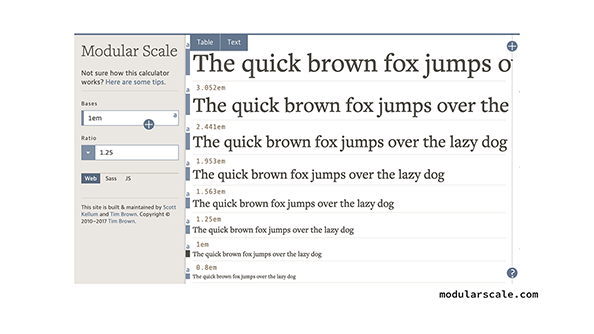
文字サイズのスケールを考えるときに役立つ手法として「モジュラースケール」というものがあります。スケールの各サイズを経験や勘にもとづいて決めるのではなく、意味のある一連の調和した比率をもとにしようというものです。これは文字サイズに限らず、たとえば本のページの縦横比やグリッドのカラムなどにも使われるものです。
モジュラースケールは音階のようなもので、あらかじめ用意された、一連の調和したプロポーションです。それは言わば、目盛りが一定ではなく、寸法が均一ではない物差しです。
Robert Bringhurst『The Elements of Typographic Style』
ブリングハーストは、モジュラースケールを「物差し」にたとえて説明しています。物差しは、目盛りが1mm単位で長さ30cmといった具合に、目盛りが一定間隔で並んでいて寸法が決まっています。しかし、モジュラースケールというのは目盛りが一定間隔ではなく、かつ寸法も自由に伸び縮みさせられる物差しだ、とブリングハーストは言っています。
また彼はその書籍の中で「モデュロール」という寸法体系にも触れています。モデュロールとは、建築家のル・コルビュジエが考案した、人体と黄金比にもとづいた寸法体系で、どうやらこれがモジュラースケールのもとになっているようです。
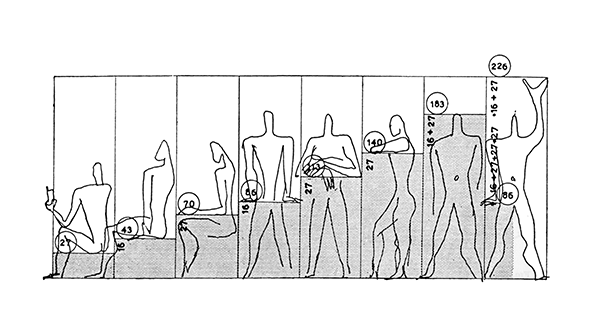ル・コルビュジエ『モデュロール』
モデュロールは、人間の身長とヘソの位置、そして手を上げた高さなどが黄金比になっているとして、これらをフィボナッチ数で分割して作った寸法体系です。ル・コルビュジエはこのモデュロールをもとに、建物だとか家具だとかを作りました。このモデュロールにおける黄金比のように、なんらかの調和する比率をもとにスケールを作り、そのスケールをタイポグラフィのガイドラインとしよう、というのがモジュラースケールの考え方です。
実際にモジュラースケールを作る場合、最初に基本となる文字サイズを決定します。まずはウェブブラウザのデフォルトである16pxとしてみます。次に、その基本サイズに掛け合わせる比率を決めます。ここでは1.25としています。この比率が大きいほど、文字サイズ間の差が大きくなる、いわゆるジャンプ率が高くなるということになります。その結果このような一連のサイズが得られるので、この中から各要素に適用するサイズを選びます。たとえば本文が16pxで、大見出しが39.0625px、キャプションは12.8px、という具合です。
こうして見ると小さいサイズから大きいサイズまできれいに並んでいるように見えます。しかし、実際にこのスケールを使ってみると、あまりうまくいかない。とくにベースの本文サイズの周辺にバリエーションがないと使いづらい。ではベースのサイズに掛け合わせる比率をもっと細かくすればいいかというと、今度は大きいサイズで選択肢が増えすぎてしまって、サイズ間に差が生まれにくいスケールになってしまいます。
いま作ったモジュラースケールは、ベースの文字サイズに対して一定の比率を掛け合わせてできた「等比数列」です。これは隣り合う項の比率がつねに等しい数列。どうもこの等比数列が、文字サイズのスケールには合わないのではないか。そこで登場するのが「調和数列」です。
調和数列というのは各項の逆数を並べると等差数列になる数列です。ピタゴラス音律や倍音など「ハーモニー」に関連していることから調和数列という名前で呼ばれています。
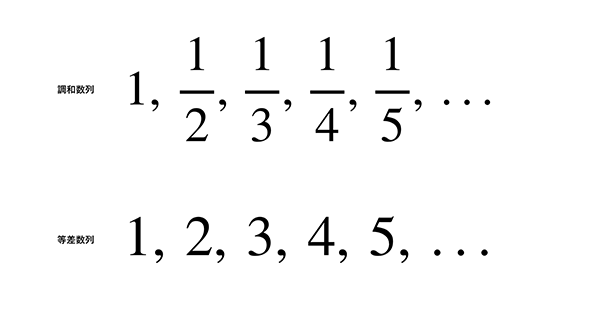
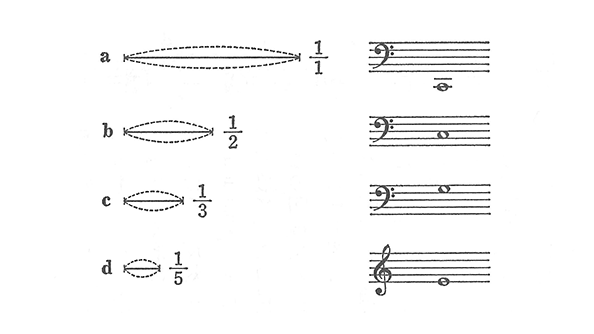
数学的な定義から見ていくと、図の上が調和数列、下が等差数列です。調和数列の例は1、1/2、1/3、1/4というように、分数のかたちをしています。これらの分数の逆数、つまり分子と分母をひっくり返すと、下の等差数列になります。等差数列というのは隣り合う項の差がつねに等しい数列です。この例では1、2、3、4と隣り合う項との差がつねに1です。このような等差数列の各項の逆数を並べると調和数列が出来上がります。この調和数列は、音楽に由来するものです。
ギターやヴァイオリンといった弦楽器を想像してみてください。ある弦の開放、つまりフレットを押さえずに弾いた音が「ド」だったとします。次に、弦の長さの半分のところを押さえて弾きます。すると弦の音の鳴る部分の長さは1/2になる。これが何の音になるかというと、さきほどの「ド」のオクターヴ上の「ド」の音になるのです。今度は弦の長さの1/3のところを弾く。すると「ソ」の音になります。このように弦の長さを1/2、1/3、1/4というふうにどんどん短くしていく。こうして得られた音と弦の長さを並べると、下の図のようになります。
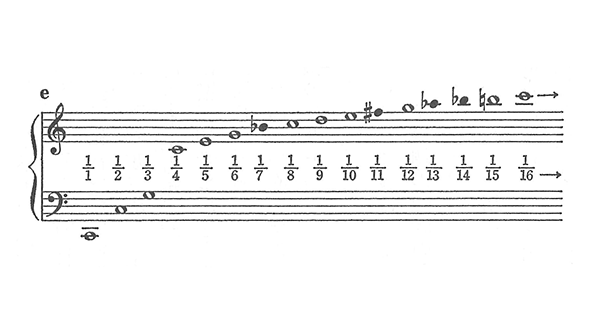倍音列
この音階は「倍音列」と呼ばれるものです。楽器や人の声は、たとえば「ド」の音を出していてもドの音だけが鳴っているわけではなくて、同時に色んな音程の音がごく小さく鳴っている。このように基準となる音のほかに鳴っている音のことを倍音といいます。この倍音のうち、どの音が大きくてどの音が小さいかといったことが楽器によって異なり、それが音色に関係してきます。さきほどギターの弦の押さえるところを変えて得たこの音階が、まさにこの倍音の構成になっているのです。
また、この倍音列の構成音を順に見ていくと、低い方から順にド、ド、ソ、ド、ミとなっていて、「ドミソ」という音のグループが表れます。このドミソというのはCメジャーのコード（和音）の構成音です。これはギターでまず最初に習う基礎的なコードです。
つまり倍音というのは、ある音を鳴らしたときにかすかに鳴って豊かな音色を作るものであると同時に、それらを抜き出して同時に鳴らせば美しく調和する和音のもとになるのです。そういった理由で、このギターの弦の長さにあたる1/2、1/3、1/4という数列は調和数列と呼ばれています。
この調和数列を文字サイズのスケールに当てはめてみます。基準の文字サイズ16pxに1/2、1/3、1/4という分数をそのまま掛け合わせると、小さいサイズしか得られませんので、さらに一定の整数を掛け合わせます。ここでは8を掛けていますが、この数字はなんでもかまいません。この数字が小さいほどスケールは大雑把になり、大きいほど目が細かくなります。
この図の上が「調和数列にもとづくスケール」で、下が「等比数列にもとづくスケール」です。調和数列のスケールはサイズが小さいほど密で、大きいほどまばらになっているのがわかると思います。等比数列のスケールにあった、さきほどのベースサイズ周辺のバリエーションが足りないという問題が解消されました。
調和数列をもとにした文字サイズのスケールにはもうひとつ特徴があります。それは日本語や中国語など、全角文字を並べたときに、図のように数文字ごとに幅が揃うということです。たとえば、本文8文字と、見出し3文字、キャプション10文字が同じ幅になる。
ハーモニーの例として、文字サイズのスケールに調和数列を応用する手法をご紹介してきました。しかし、調和数列にもとづいているからこれは美しい、読みやすいなどと因果を逆転させることはできません。重要なのは、それぞれのサイズが意味ある比例にもとづいた秩序でデザインされているという事実なのです。
リズム
次にリズムです。リズムはあらゆる音楽の出発点であると言われ、まさに音楽の核をなす要素です。音楽というのは時間の芸術です。リズムが止まるとき、音楽もまた止まります。またハーモニーやメロディのない音楽は想像できますが、リズムのない音楽というのは想像できません。たとえばアンビエントとかフリージャズとか、明確なビートがなかったり、ビートが不規則だったりするとしても、それが音楽である以上は必ずリズムが存在しています。
タイポグラフィには縦のリズム、「ヴァーティカル・リズム」という概念があります。これは横組である欧文のタイポグラフィに由来する概念で、行の折り返しによって生まれる行間や、要素間の余白に一貫性があるかどうか、という視点です。この縦のリズムに規則性がないと、読みづらかったり、情報のヒエラルキーが正しく伝わらなかったりします。これはビューが縦方向に長くなるスマホではとくに重要な視点です。本の組版では本文（ボディテキスト）の行送り、CSSでいうところのline-height（行の高さ）が縦のリズムの基準になります。
たとえば、このようなページなどの本文部分。本文の行送りが28pxだとしたら、段落間の余白はその1行分の28px、中見出しの上は2行分の56pxアケる、といった具合です。しかし実際のウェブサイトやアプリケーションでは、このようなシンプルなビューだけではありません。
次の例は、ニュース記事などで使用されるカード型のUI（ユーザーインターフェース）。この小さなカードの中だけでも複数のサイズのテキストがあり、情報の主従関係や重要度といったヒエラルキーがあります。またカードを複数並べるときのカードどうしの余白や、見出しの上下の余白などにも注意を払う必要があります。この場合、本文の行送りだけを単位にしていては、とてもレイアウトできません。
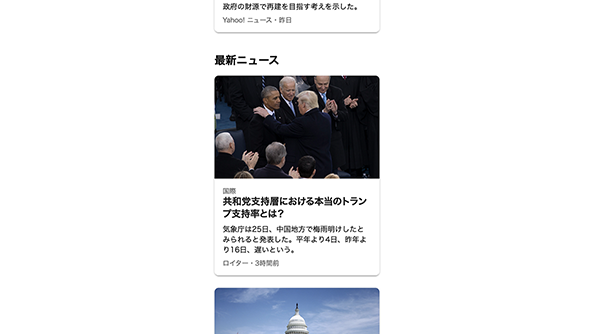
ではどうするかというと、リズムを構成するビートを細かく分割して、状況に応じて組み合わせるのが有効です。いわばシンプルな4ビートだったのを16ビートにするような、そんなイメージです。テキストの行送りは4px単位、コンポーネントのスペーシングは8px単位、そしてさきほどのように本文は行送り単位、という3つのスペーシングユニットを組み合わせる手法を紹介したいと思います。
4pxグリッド
まず4pxグリッド。これがすべてのリズムの最小単位になります。これはテキストの行送りに適用します。つまり、すべてのテキストのline-heightの計算値が4pxの整数倍になるようにします。
カード型のUIを例に考えてみましょう。ここにはラベル、タイトル、ディスクリプション、メタデータといった、文字サイズの異なる要素が並んでいます。
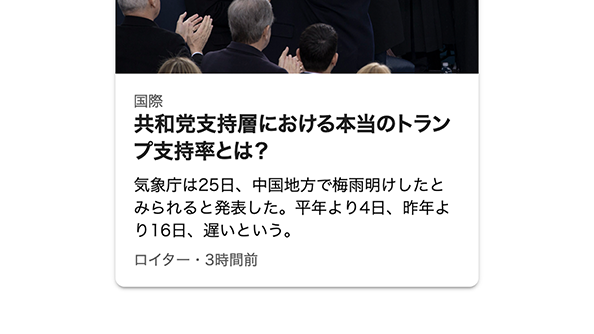
これらをこのように、すべてのテキストの行送りを4px単位に揃えます。最小単位は必ずしも4pxでなければいけないわけではないですが、計算のしやすさや、最適なサイズを考えて、取り扱いやすい4pxを行送りの単位としてみました。
CSSでは、すべてのline-heightが4pxの整数倍になっています。
8pxグリッド
次に8px単位のグリッド。コンポーネント内のスペーシングや、コンポーネントどうしのスペーシングが8pxの整数倍になるようにします。とは言え、8px単位でどのように配置してもいいとなると、システムとして一貫性のないものになってしまいます。そこでさきほどの文字サイズのスケールと同様に、あらかじめ使うべきスペーシングを「スケール」として定義しておくのがよいでしょう。
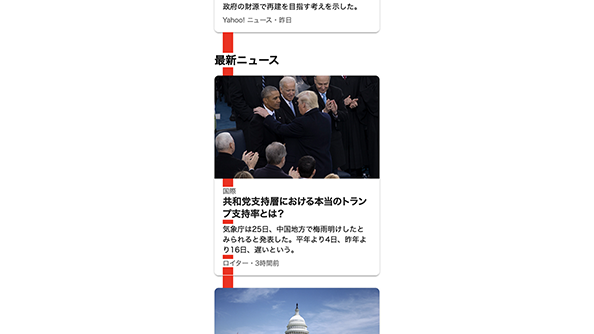
たとえばさきほどのカード型のUIが並んだ画面。見出しの上下のスペーシング、カードどうしのスペーシング、カード内のテキスト間のスペーシング、それらすべては互いに影響しあって情報のヒエラルキーを表現しています。これらを8pxを単位に配置するとき、どのようなスペーシングのスケールを定義すべきかについて、いくつかのパターンを考えてみたいと思います。
もっともシンプルなのは、8pxを2倍、3倍、4倍……と大きくしていくパターン。その結果出来上がるのは8px、16px、24px……というスケールです。
このスペーシングを図にするとこのようになります。これでは大きいサイズになったとき、スペーシング間の差があまり感じられず、コンポーネントによって使うスペーシングにばらつきが出てしまいます。
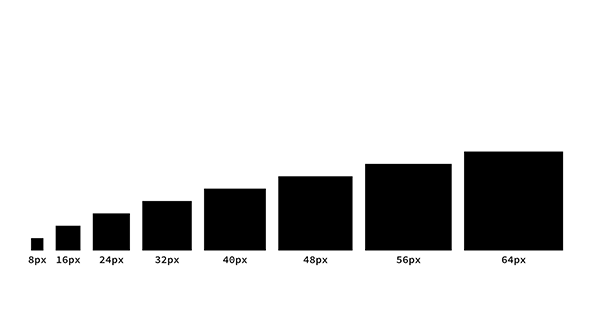
次に8pxのユニットを16px、32px、64px……と2倍に増やしていくスケールです。これでは差が極端になって、実用性がないのがひと目見てわかります。
スペーシングスケールの最適化
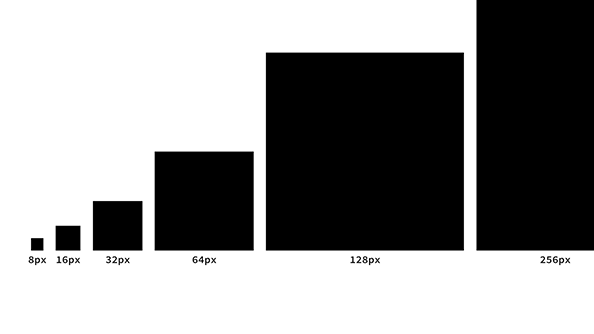
どのようなスペーシングスケールが最適なのか。それは8pxのユニットに1、2、3、5、8、13というフィボナッチ数を掛け合わせていったものです。
フィボナッチ数列は、1, 1, 2, 3, 5, 8, 13, 21, …と続き、各項の値が前の2つの項の合計になっています。そして隣り合う項の比率がどんどん黄金比（1.618）に近づいていくという特徴があります。
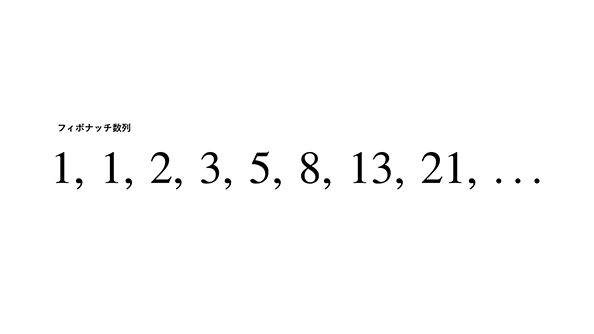
フィボナッチ数を使ったスペーシングのスケールを利用すると、サイズ間の差が大きすぎず小さすぎず使いやすい。
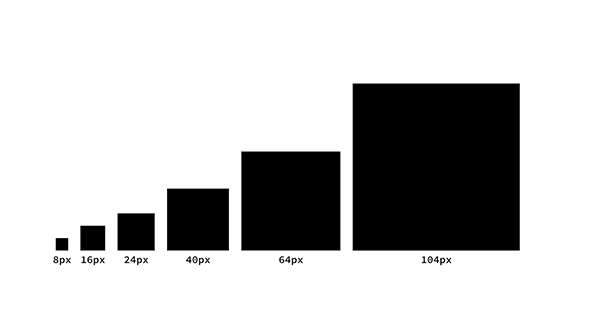
さきほどのカードUIの例に、8pxにフィボナッチ数を掛け合わせたスケールでスペーシングを構成してみるとこうなります。
本文の行送りだけですべてのリズムをコントロールするのは無理があるので、いくつかのスペーシングユニットを組み合わせること。また、ただユニットに沿わせるだけではなく、そこに一貫性を持たせるためにスペーシングスケールを作ることが、タイポグラフィにおける縦のリズムにとって大事なのです。
メロディ
最後に音楽の3要素の3つめ、「メロディ」について。メロディの語源はギリシャ語で「歌うこと」を意味する「メローディア（melōidíā）」という語で、このメローディアという語はさらに「歌（mélos）」と「詩（ōidḗ）」という2語の合成語です。音楽のルーツがどういうものであったのかということについては諸説ありますが、メロディは語源に「詩」があり、どうやらそのルーツは「言葉」なのがわかります。まず伝えるべき言葉があり、それに節をつけて歌ったものがメロディなのです。
ここでの結論は単純です。メロディのルーツが言葉であるように、タイポグラフィにとってもっとも重要なものも、やはり言葉ということです。どのようなタイポグラフィも、伝えるべき言葉が最初にある。言葉で書かれたコンテンツを届けるということは、歌手が歌うということであり、ピアニストがソロを弾くということです。そのときタイポグラフィに求められるのは、そのメロディを力強いリズムと美しいハーモニーで支えること。よい伴奏者、優れたバックバンドであることだと思います。
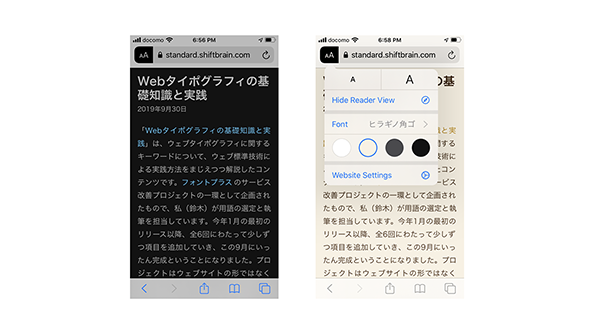
この画面は、iOS Safariのリーダービューです。ウェブサイトのスタイルをプレーンなかたちにリセットして、書体、文字サイズ、カラーなどをユーザーが選択して読むことができます。同様の機能はChromeやFirefoxなど多くのウェブブラウザで、モバイルでもデスクトップでも提供されています。このようなビューでは、デザインしたタイポグラフィが無効になるわけです。
しかし、これこそがオンスクリーンメディアにおけるタイポグラフィのもっとも素晴らしい点です。ユーザーにとって読みにくい書体があったり、見えにくい色があったりしても、その障害を乗り越えてコンテンツを届けられる可能性がある。そして、このようなアクセシビリティを支えているのがHTMLというものです。コンテンツが適切にマークアップされているから、アクセシビリティの提供が可能になる。
それなら最初からユーザーにすべて設定させればいいじゃないか、と思う方もいらっしゃるかもしれません。たしかにすべての人にとって読みやすいタイポグラフィは不可能かもしれませんが、それでもタイポグラフィを追求することには意味があります。
開かれたタイポグラフィのために
タイポグラフィには文字によって情報を伝達するという明白な義務がある。いかなる議論や考察も、タイポグラフィをこの義務から解放することはできない。読むことができない印刷物は、目的を失った制作物である。
エミール・ルーダー『タイポグラフィ※6』
これはエミール・ルーダーが印刷物のタイポグラフィについて語った言葉ですが、オンスクリーンのタイポグラフィにも適用できます。すべてのタイポグラフィは、より多くの人に、より間違いのないかたちで、よりわかりやすく、そしてより美しく「伝える」ためのものなのです。
わたしがオンスクリーンメディアのタイポグラフィに取り組みはじめたときには、音楽や数学の理論を参照するとは想像していませんでした。ここにたどり着いたのは、制作の現場で直面した具体的な課題を解決しようとした結果です。異なる文字サイズのテキストをうまく配置できないかとスケールを試行錯誤するうち、いつしか数列のようなものが導き出され、それはどうやら音楽に由来する調和数列らしいことがわかるといった具合に、少しずつかたちをなしていきました。これは楽典を学んでから音楽を聴きはじめる人がいないのと同じかもしれません。
タイポグラフィの作業をしていると、いつしか偏執的に細部を追求しています。その度に、独りよがりの美意識を読み手に押しつけているのではないか、誰も望まない完璧さを求めているだけではないのか、と不安になります。そういったときに、タイポグラフィの歴史を見つめ直したり、音楽や数学などの知恵から学ぶようにしています。その理由は、すでに完成された世界を新しいメディアで再現したいからではありません。これは、まだはじまったばかりのオンスクリーンメディアのタイポグラフィの可能性を、より開かれたものにするための試みなのです。
