「秩序」という言葉を聞くと、どうしても最短距離でたどり着ける有益で近代的な秩序が思い出される。それと同時に、それ以外の役に立たない「無秩序」も想像されるかもしれない。しかし、宇宙が成り立っている以上、ずっと「秩序」はあったわけで、それは限りなく広い「野生の秩序」と言える。近代的な意味での秩序が、ゲージで飼われたペットだとすると、野生の秩序は動物の種全体のようなものかもしれない。だから、人間には飼い慣らせないし、簡単に手も出せない。だがしかし、それはたしかに「在る」のだ。
私はこの「野生の秩序」の端を、数学で覗き見たのかもしれない。それは高度で専門的な数学でなく、その入り口にあった※1。
「これは詩なんだ」と思って読んだ。詩だから何かに役立てようと思って読む必要はない。科学の源である数学だが、私は役に立つことより詩として美しいなと感じた。すべてを読んで理解することは難しかったが、自分はただこの海を漂う泡のようなものだと思いながら、詩を楽しんだ。
§
たとえば登山をするときに、私は装備を整えて目的の山に向かっていくことが難しい。そう考えると、簡単にへこたれてしまう。
それよりも、歩きながら、こんな石ころがある、草が生えている、落ち葉がある、水の音がしてるから、この先には沢があるなと想像したり、こんな花が咲いてるとか、足下を見ながら歩いていたら、あるとき峠に出る※2。そこには初めて見る景色が広がっている。そこで出会うのが、私にとっての作品になる。
それは、多くのものが連動して変化し続ける世界で、ある絶妙のバランスが取れたときに心地のよい像が出現する、そんな景色。それは固定されたものがなく、どこにも中心がない。ただ共に揺れる「感度」が、生命のように広がる姿。
今回展示される資料やノートは、私が見てきた石ころや落ち葉や野花たち。そのなかには、渡れぬ沢もあったが、その道のりは楽しかった。
§
1980年代中頃にパーソナルコンピュータが市販されはじめ、当時グラフィックデザインの仕事をしていた私は、奇麗な形がディスプレイに現れるソフトウェアの簡便さを前に、ただただ困っていた。描出の身体は、どこに棲み直すのだろうか、と。
コンピュータはプログラムによる命令を順次実行する。物質としての線が在るのではなく、線を定義するコードがある。それを視覚化するコードがある。形態というものを、生成の定義で捉え直す。
そして、新しい視覚表現は、見えている形態よりも、それらを生成するメカニズムの方にあると思うようになり、プログラムをはじめた。それは普遍的な記号と演算であり、私自身から出発できないことも、ひとつの覚悟になった。
最小単位のピクセルがある。解像度を上げて人の目に滑らかに見えたとしても、そこには最小単位の「刻み」がある。最初に違和感を持ったのは、これだった。道具はデジタル(離散)でも、イメージはアナログ(連続的量)だ。もともと連続量としてある世界を、ここでは離散の値で取り出しているのだ。
私が新しい表現として興味を持ったのは、形態よりもそれを生成する変化や動きであり、その記述方法は運動方程式を作って走らせることだと知った。それはこの離散の背後にある連続性を知ることからだと思った。
だから、最初に取り組んだのは「実数の連続性」だった。そこから「連続関数〜運動方程式」へ、そして「座標」の変換と写像に出会うこととなった。
ここからの説明は、視覚表現者としてコンピュータメディアと関わっていく上での基盤になった大まかなイメージである。つまり、数学書を正確に読めたかどうかではなく、このように掴んでみたという話になる。
実数の連続性
これは、数は連続であるか、それが事実かどうか、という問いではない。「連続」と「無限」の世界に入って行って、「実数の連続性」という概念が掴めるかどうか。
直線上に有理数(分数で表せる数)を置いてみると、そこに順序ができる。しかし、長さという「量」を計ろうとしたときに、有理数に収まらない「数」が現れてくる。ピタゴラスの定理で直角三角形の斜辺の長さとして現れるあの√2という無理数だ。こうした無理数は無数にある。数と図形を対応させるにはどうしても「数の連続」が必要なのだ。
ここに「デデキントの切断」というアイデアがある。直線上には大小の順序があるので「切断」によって上組と下組の2つに分けられる。
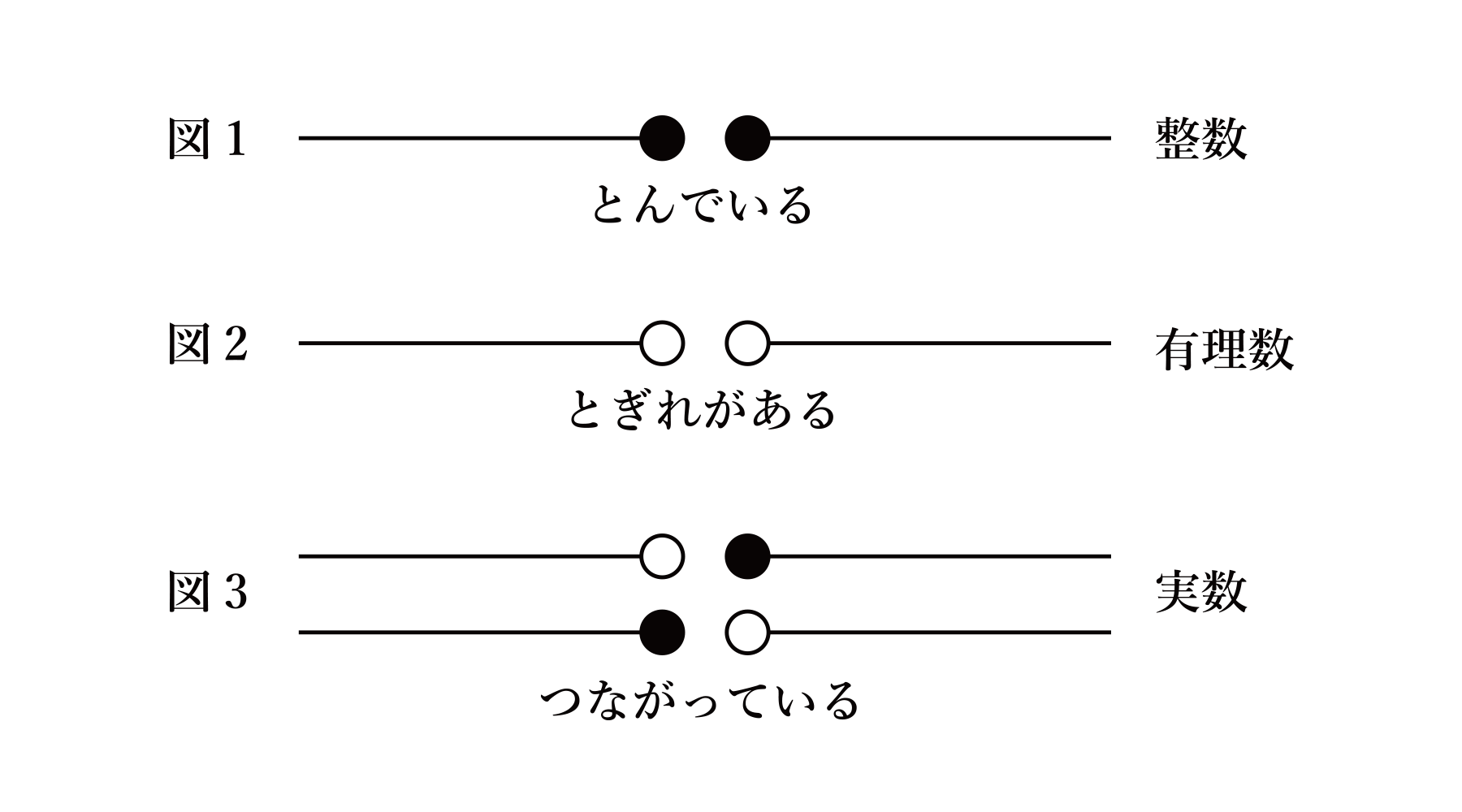
図1は自明だろう。たとえば無理数√2より小さい数と大きい数に切断すれば、図2のような途切れが出てくる。どちらも直線と同一視はできない。有理数と無理数から成る実数を、図3のような切断面(上組と下組の境界)に必ず「数」がある、と定義する。どの切断面にも「数」がある。
切断によって2組に分けられ、その切断面のところに数があるというアイデアに感銘を受けた。これは理解することではなく、頭の中に連続性が棲んでいるという認識になり、連続という概念が定着した。ここで私は、数学が知識や道具ではなく、思考の楽しみに変わっていった。
連続関数〜運動方程式
実数の連続性から、有界、上限、下限、収束、発散、振動を経て、「有界な単調数列は収束する」という定義に至る。それは、限りなく近づき行き着く何か=最小下界(下限)をどう頭の中に存在させるか、という問題になる。その値に限りなく近づき、そこでピタリと止まる値がある。この行き着く先=極限値が「在る」という確信。ある種のリアリティだ。
連続関数の1つの点での動きの変化量を捕まえて行く。ある点の運動をある範囲で考えると、どの程度変化したのかという平均変化率が出る。この範囲を限りなく0に近づけたときの値が微分係数となる。これは平均変化率の極限値として存在する。すると、連続関数の各点に微分係数を対応させる関数ができる。その関数は導関数と呼ばれ、これが変化の記述になる。
運動する点の位置から、速度(導関数)、加速度(2階の導関数)が定まり、運動方程式(微分方程式)が構成される。そして自分で表したい動きの方程式を作れるようになった。
実数の連続性から、変化の記述の意味と実在感が現れる。目に見えるのは離散のディスプレイであるが、制作する心には「連続性」がある。動いて行く数を表示していくときに、それを保証する人間の思考のおもしろさを感じた。微分係数は、ちゃんとそこに存在する。デジタル値やディスプレイの解像度によって桁は切り捨てられても、その正体のようなものはある。
そこからさらに、動いていく数を表示する空間は、天与に固定されているのか、空間とは何か、といったことに興味は続いて行った。
座標
普通座標と言うと直交直線のユークリッド座標を想定するが、果たしてそうだろうか。数学の入り口で、全く異なる様相がみえた。
ユークリッド空間では、平面の1つの点はp=(x1,y1)という2つの数を使って示すことができる。平面はこのように2つの実数の組で表せる点の集合である。たとえば、3次元とは3つの実数の組、n次元ならn個の実数の組になる。空間の各点はベクトルで示すことができる。これが位置ベクトルで、これによってユークリッド空間で幾何と数が結びついている。
しかしこれを連続性から見て行くと、2つのベクトル(位置)には「距離」がありここから近傍、収束と進み点の集まりのその各点に近傍系が定義されている、ただそれだけの位相空間という考えに至る。座標の入った位相空間を考えると、ユークリッド空間はその中の使い易い1つにすぎなかったのだ。これは非常に大きな転換点だった。
そのとき、遠い幼少期の記憶が蘇った。自分のまわりにはいろんな空間があった。海水浴をする、昆虫採集をする、朝顔を育てる、レコードを聴く、本を読む、ネコと遊ぶ。そんなことがいつもあった。これらの空間は、それぞれ別のものだが、互いに無関係ではなかった。そう考えると、あらかじめ用意されている空間のどこかに自分の場所が固定されるという気持ちは消えていった。ただどこまでも続く広がりがあり、それぞれの場所にはその周辺があり、それらが関連しあって流れ動いていく景色が見える。
位相空間Xから位相空間Yへの写像y=f(x)とは、Xの点xに対しY の点yが「一通り」に決まることをいう。逆に言うと、こうした一通りにきまる規則を作ればいいだけなのだ。位相空間Xを使い慣れた直交直線座標の入ったユークリッド空間として、そこから全ての点が重複せず一通りに決まる座標であればいいのだから、座標の入れ方は無数にある。
数を実数の世界から複素数の世界へ拡張すれば、2次元から2次元への変換は等角写像として使いやすいものが多く用意されている。使いやすいユークリッド空間で作った運動の形も、写像という方法でどのようにも変形できる。また写像は何回施してもよいわけだ。
具体的な物理現象を記述するのではなく、ヴィジュアルとしてユニークな運動を抽象的に構成していく上では、危険もあった。身体から離れて、技術的に可能なことを勝手にやってしまうと、自然や経験からは到底出て来ない気味の悪さに溢れてしまう。だから、人間、自然、身体を痛いほど思い知ることとなった。生き物の奇跡を思わされた。
実際の描出のステップは、運動の計算に加え視覚的な工夫の計算もあるので、ディスプレイに直接描出はできない。小さいデータサンプル群を作り、像をイメージしながら、パラメータ値を決めて、実際のサイズで演算させる。一晩経って、たとえば3000カットがメモリに書き込まれる。それをPICTに起こし、レンダリングすると、初めて2分程度の動画になる。
現れた動画は、イメージしていたものと骨格は同じでも、表情はずいぶん違う。窯を開けてはじめてわかる、陶芸の焼き物のようだ。むしろ初めて見る像である方がいい。それをいくつも作って、できたものから選んで、それらを繋いでいく作業が続く。では、このように膨大に出現するディスプレイの像から、作品として取り出すときの選択は何に拠るものだろうか。
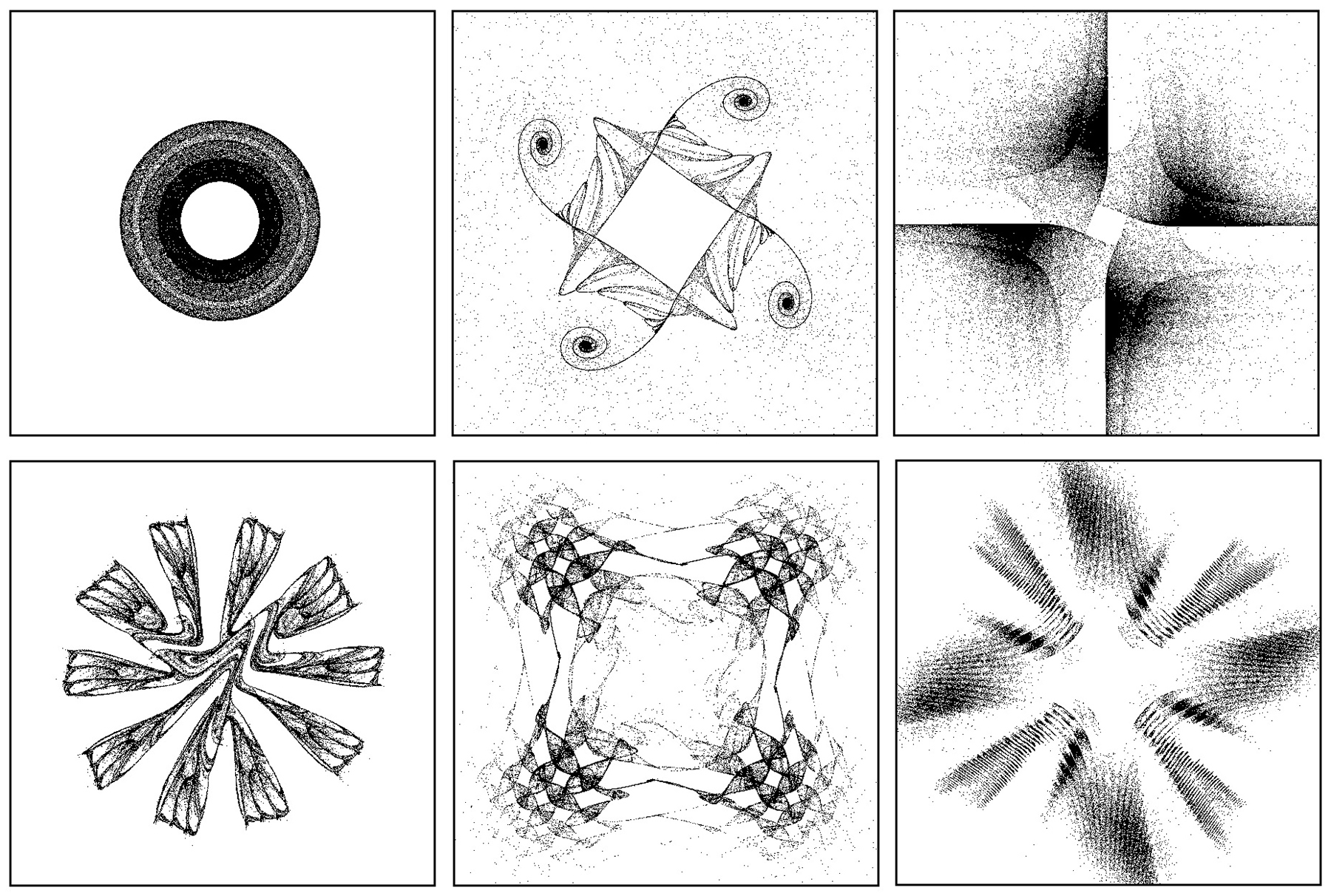
ここまで抽象的に進めてきて、せっかく連続の世界で、「私」というものの「硬さ」を砕いてもらったのに、最後に「自分の好み」が出て来てはおもしろくない。だが「私」を全く排除することも不可能だろう。ここは今もわからない。ただ、「私」というものにこだわりなき心地よさを探して行くということなのだろうか。「私」が粉々に小さく砕け、広がりのなかを動いて行くというイメージを持つこともできるが、それが実際にできるわけではない。
最後に
ここまで、私が接してきた数学のことを書いたが、まだどれも入り口だと考えている。いろんな数学書(解析や多様体や複素解析など)を読んできたが、その最初の数十ページの基礎の思考が重要だった。その先に、万華鏡のような綺羅びやかな数学の世界が広がっていくことも想像できる。しかし、それは美術人の理解の範疇ではない。
それよりも私にとってかけがえないことは、その入り口にある精密な思考、そこから生まれる広大で「自由」なアイデアだった。改めて、それは感性の塊のような「詩」だとも思う。その自由さに圧倒されながら制作を続け、自分の狭かった心も広がっていくことが、何よりも嬉しかった。
[構成:多田かおり(東京都写真美術館)、編集:大林寛(ÉKRITS)]

