ここまでの流れ
VECTIONでは、本稿に先立つ二つのエッセイを発表している。そこでは、権力の暴走を防ぎ、フェアな権力分立を維持するための条件をあげた。①絶対的な権力者を認めない。②第三者機関の中立性をあてにしない。③権力を監視する者を監視する者を監視する者…といったメタレベルの無限後退に陥らない。という三つだ。そしてこの、王様もなく、外部もなく、メタのメタもない、という条件を可能にする権力分立は、どのような形式であれば可能であるか検討するなかで、一般に「三権分立」と言われているものは、実質的には「政府」と「国民」の二層（レイヤー）となっていることを示した。
二つのレイヤーによる権力分立では、互いが互いに対して利害関係にあるため相互監視をフェアな状態に保つことが困難だと予想される。そこで、「国民」「政府」の他に、「世界」というレイヤーを加え、この三者が互いに制御し合う形をとる権力分立のあり方を提案し、これを「3（スリー）レイヤーサイクル」と呼んだ（「世界」とは、「国民」と「政府」以外のすべての外部性を含むレイヤーで具体的には、外国や地球環境などが所属する）。3レイヤーサイクルは、三権分立とは異なり、局所的には上下関係が決まる。だが、全体としては上下関係を決定できないという、エッシャーの無限階段のような構造になっている。3レイヤーサイクルによって、王も外部もメタのメタもないという条件を表現することができる（以上、「権力分立と希望の幾何学※1」）。
ここで、「国民」「政府」「世界」を、一般に想像しやすい「アクター」ではなく「レイヤー（層）」としている。レイヤーは、Photoshopという有名な画像編集ソフトなどで、描画領域に対してフィルターを層として重ねることで画像を構成する概念であり、そのイメージを借りている。また、レイヤーから別のレイヤーに対する権力の行使を意味する矢印を、同ソフトでレイヤー間を縦に貫く働きを意味する「チャネル」という比喩で表す。詳細は「権力分立と希望の幾何学」を参照してほしい。
3レイヤーサイクルによる権力分立を維持するには、サイクルの「劣化」を防ぐ必要がある。つまり、権力の不均衡（一方的な優位化、階層の形成）やレイヤー間の癒着や切断を避ける仕組みが求められる。この点について、VECTIONでは「壺の断面が歪むとき ー 権力分立と希望の幾何学 #2※2」というエッセイを著した。
状況によっては一時的な権力の不均衡は許容されると考えられる（テンポラリーフェアネス）が、それが固定化されると諸々の問題（劣化）が生じる。そして、どのような状況ならば不均衡が許容され、どの程度の期間であれば許容されるのか評価する必要がある（フェアネス評価）。更に評価を誰が行うのかが問題となる。このとき、冒頭に述べた条件③より、「第三者委員会」のようなレイヤーサイクル外部に存在する客観性は信用できないと考える。だとすれば、利害関係者以外で、かつレイヤーサイクル内に存在するレイヤーが、その評価を行うしかない。前稿「壺の断面が歪むとき※3」において、VECTIONは、権力の循環構造が崩れる原因と、レイヤーのフェアネス評価によるサイクルの回復について詳細を議論した。
しかし、完全に利害関係のないレイヤーは、3レイヤーにおいては存在しえない。本稿ではその問題点を指摘したのち、レイヤーの数を増やすことに対し検討を重ね、評価者の中立とレイヤーサイクルのシンプルさを両立するレイヤー数が5であると主張する。
なお、上で要約した二つのエッセイは、本稿での考察から派生して生まれたものであり、本稿で扱ったことがらのダイジェスト版という性格もあるため、本稿では上記のエッセイと重複する部分もある。しかし、草稿の執筆順序では、こちらがオリジナル（2017年頃にほぼ発想の原型はあった）であり、より詳細に論じている。
問題と目標
ガバナンスを理念的に分類するとき、一方の極に一人しか権力を持たない専制があり、他方に完全に分権化された直接民主制という軸がありうる。だが、歴史を振り返ると、扇動された民主制が自ら専制を選び自己否定することがしばしばある。ナポレオン三世、ヒトラーの政権獲得は古典的な事例だ。一方、権力分立は、一極集中と完全分権の相互反転を避けつつ、比較的少数のレイヤー（グループ、利益集団）によるガバナンスを、相互に暴走を抑制する形で行う方法の一つである。
ここでは、権力の相互抑制についての「良い仕組み」を見つける指針として
+ 癒着の有無や固定した権力関係の評価（＝「フェアネス評価」と呼んでおく）、を行うターゲットが、評価者の利害関係からなるべく遠くなること
他の言い方をすれば、
+ フェアネス評価が、評価者自身がターゲットに対して持つ利害関係によって歪められ、無効化されないこと
をとり、先の二つの論考で抽出した権力分立の「3レイヤーサイクル」構造が原理的に孕む難点をこの観点から修正し、より「良い仕組み」へ到達することを目標とする。
権力分立が持つ難点
以下では、前稿で検討した3レイヤーサイクルの、利点と困難について考える。
なぜ3レイヤーサイクルだったのか？
まず、トップダウン評価の難点という観点から、3レイヤーサイクルの発生理由を辿って分析するための概念を用意する。
メタ・レイヤーとオブジェクト・レイヤー
評価に伴う利害関係を定義する。あるレイヤーxの利害関係を考察するとき、「レイヤーxを制御するレイヤー」と「レイヤーxに制御されるレイヤー」を考慮に入れる必要がある。ここでは、前者を「（xに対する）メタ・レイヤーM」、後者を「（xに対する）オブジェクト・レイヤーO」、xは「（考慮するときの基準である）参照レイヤー」と呼ぶことにする。各レイヤーを結ぶ矢印が「チャネル」で、左の図11では平面上に描かれているが、イメージとしては右側の図2のように重なり合ったフレームを貫いている影響関係が矢印で表現されているので、「レイヤー」という言い方をしていると考えてほしい。
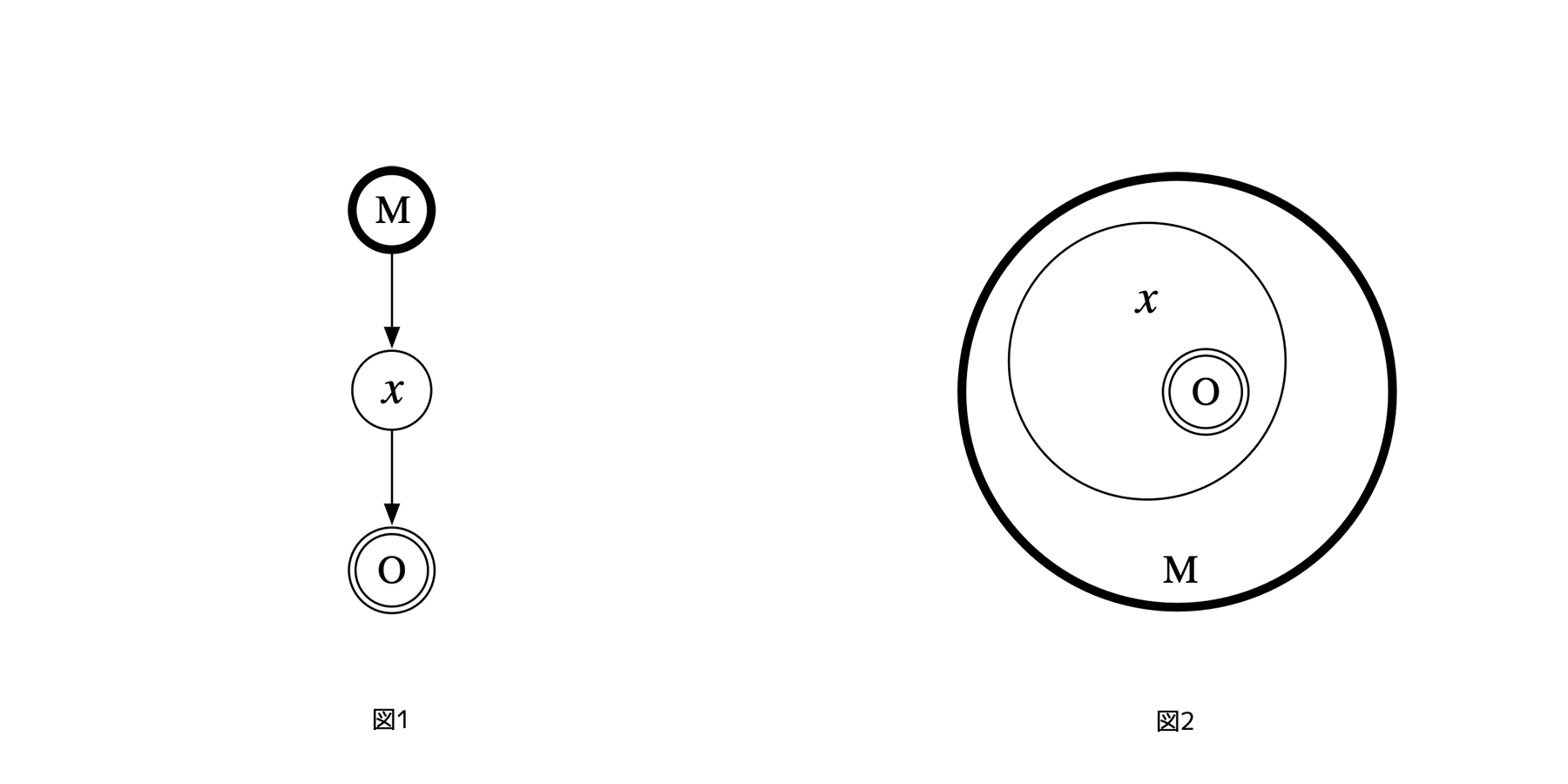［図1］レイヤーxに対するメタ・レイヤーMとオブジェクト・レイヤーO［図2］参照 (x)、オブジェクト (O)、メタ (M)の重なり合い（フレーム表現）
トップダウン評価の利点と難点
図では、メタ・レイヤーとオブジェクト・レイヤーを含む最も単純な制御構造として、「トップダウン制御」を描いている。図1では、メタ・レイヤーとオブジェクト・レイヤーは同一平面上に描かれている。なお、視点を変えれば、これらは図2にあるように、「生物＝メタ」「動物＝参照」「ヒト＝オブジェクト」のように異なる階層の概念の略記でもある。
このような評価の構造は、独裁のように、最高権力者が誰からも制御されずに、ほぼ一方的に他者を制御できる体制、あるいは、市場、株主、有権者といった、外部制御レイヤーから切り離されたときの、企業組織や政府に見られる。
トップダウン制御は、その概念的・制度的単純さ、階層を深くすることによるスケーラビリティ、最高位のレイヤーが有能な場合の効率性の高さなどから、現代の組織でも広く浸透している制御構造である。
一方、抑制のないトップダウン制御は、一番上のメタ・レベルのレイヤーが機能不全になった場合、誰にも修正できない。その難点が、多くの歴史的悲劇を生んだ。また階層が深くなった場合に起きる伝達効率の悪化、制御不能性も大きな問題になりうる。
3レイヤーサイクルの利点
トップダウン制御の難点を克服するため、以下の図3、図4、図5のような「3レイヤーサイクル」という制御構造を、「最低位の制御対象であるOに対し、最高位のMを罷免する制御を許したループ状の制御構造」として考える。
Mがxを制御し、xがOを制御する、という部分の関係はトップダウン制御の例と変わらない。しかし、トップダウン構造と大きく異なり、3レイヤーサイクルでは、最低位のO（オブジェクト）が最上位のM（メタ）を制御するという「下剋上」が起きる。この点、図をみて理解したつもりになっていても、「オブジェクト」や「メタ」という言葉の意味に影響されて間違えやすいので注意してほしい。
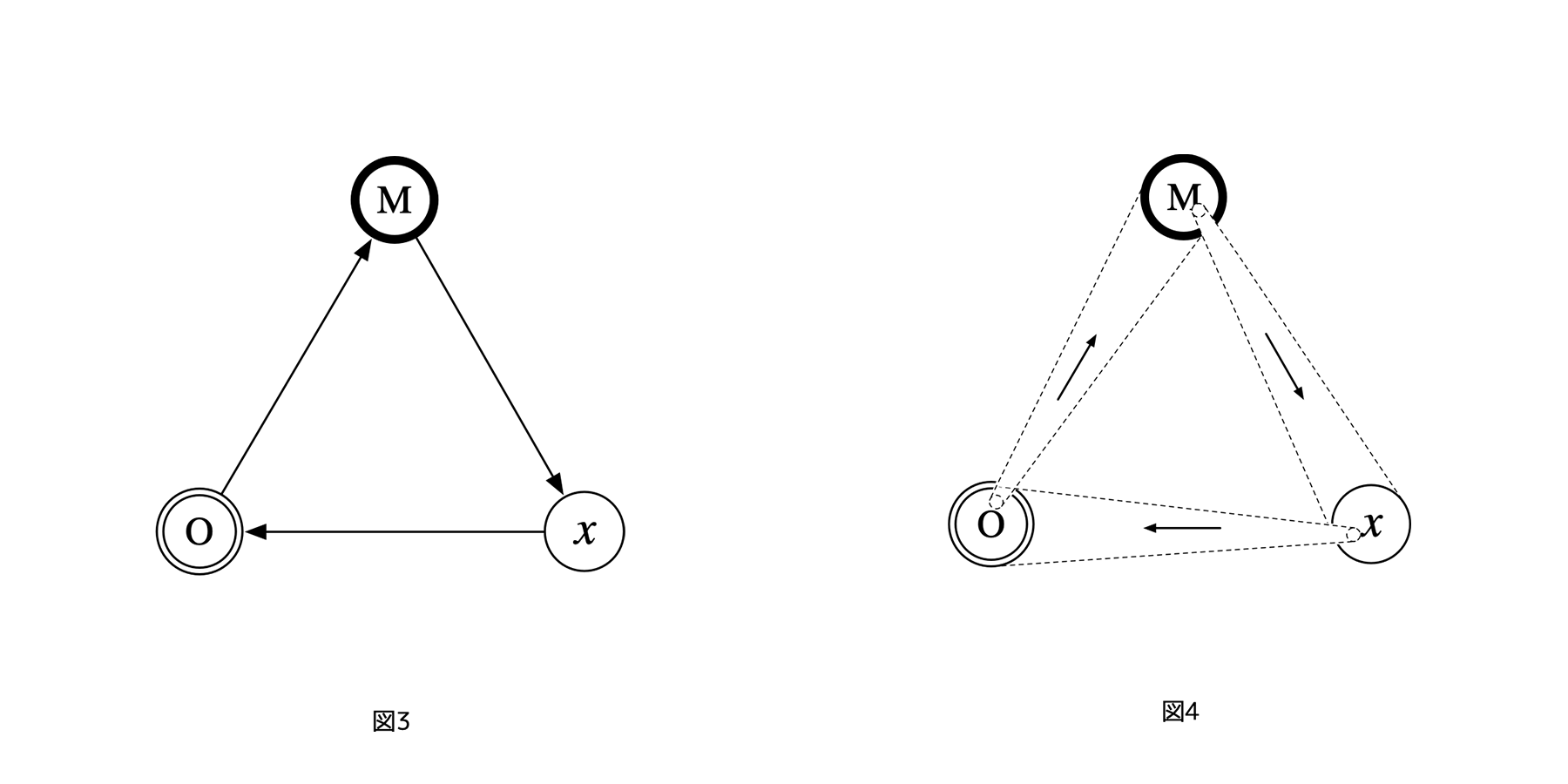［図3］［図4］
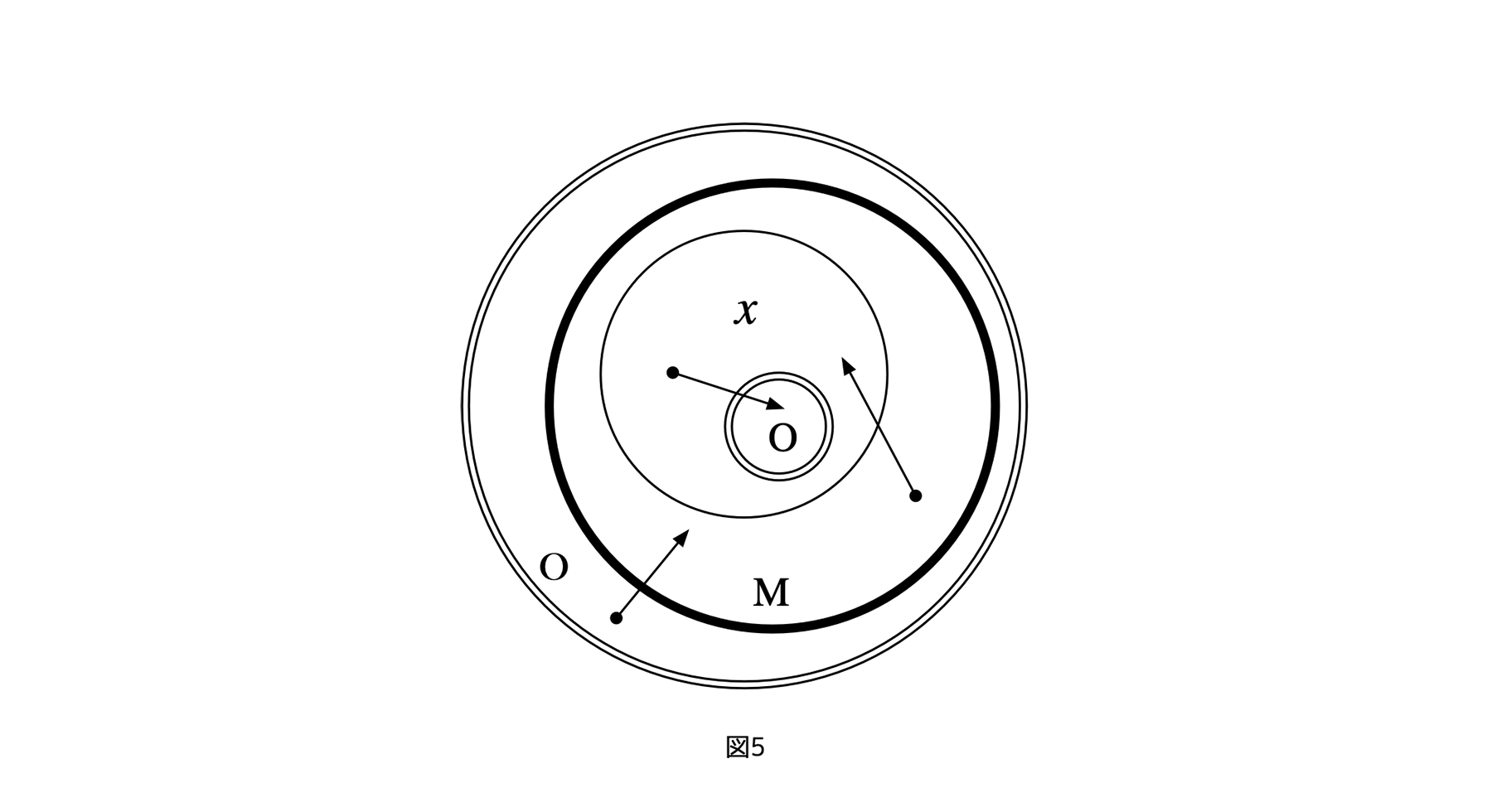［図5］
3レイヤーサイクルには
+ メタ・レイヤーとオブジェクト・レイヤーの立場が循環することで、誰かが一番上のメタ・レイヤーになることがない(局所的には上下関係があるが、全体としては上下が決められない)
という大きなメリットがある。その結果、トップダウンの「一番上位にいるレイヤーが機能不全に陥った場合、誰もそれを抑制できない」という難点が緩和される。
3レイヤーサイクルの難点
しかし、3レイヤーサイクルには難点が二つある。
+ 評価の矢印は一方向である必要がある。しかし、（メタとオブジェクトなど）隣接するレイヤー同士が「癒着（便宜、迎合）」し、双方向になりがちである
+ 一箇所でも癒着して双方向になると、事実上トップダウン（2レイヤー構造 前稿参照※4）に戻るが、それを是正する方法がない
ここで「迎合」は通常の意味より広くとる。たとえば、レイヤーOを制御するレイヤーMに対し、レイヤーOが、賄賂を送るなどの仕方で、「あなたに利益を与えるので、私への制御を甘くしてください」というシグナルを送るとする。このような、そもそもの制御方向に逆行するシグナルを送る行為全般を「迎合」としよう。
逆に、「便宜」は、本来強い立場であるはずのレイヤーが、なんらかの利益のため、本来の制御を偽り、手加減や相手の利益を優先をすることを指す。「強い立場」とは、「xにとってのM」、「Oにとってのx」、「MにとってのO」など、制御する側のレイヤーだ。
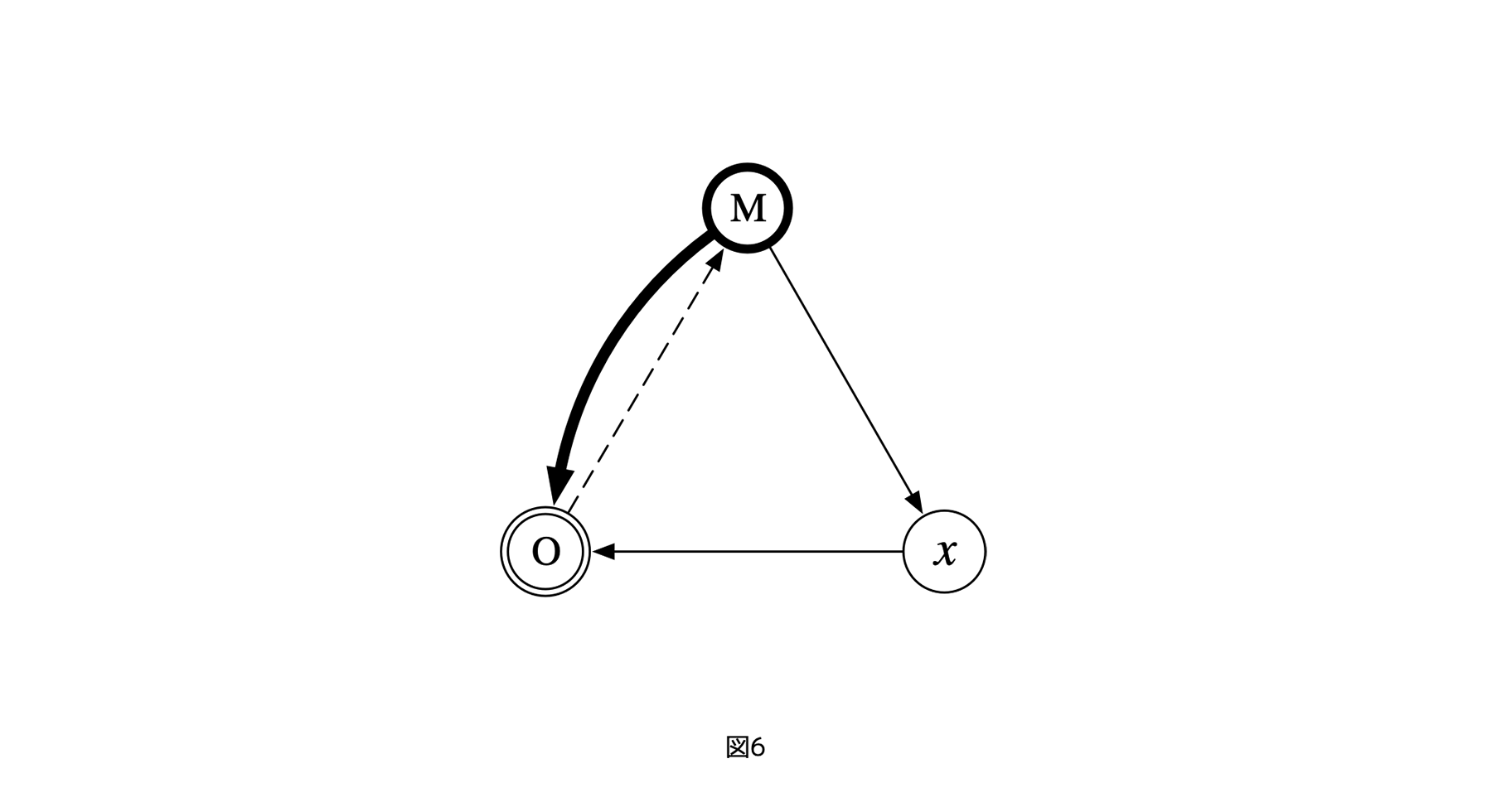［図6］制御OMの便宜への変化
図6では、本来の制御方向 ーこの場合は、O（オブジェクト）からM（メタ）なので言葉の意味とは逆になることに注意ー を逆転させた湾曲矢印MOは迎合、点線矢印OMを便宜と表現している。迎合や便宜の結果を、制御チャネルの「双方向化」と呼ぼう。
双方向化の問題点は、本来分権化するべきレイヤー群が結託することで、結託から排除されたレイヤーを、実質的にトップダウン評価できることだ。
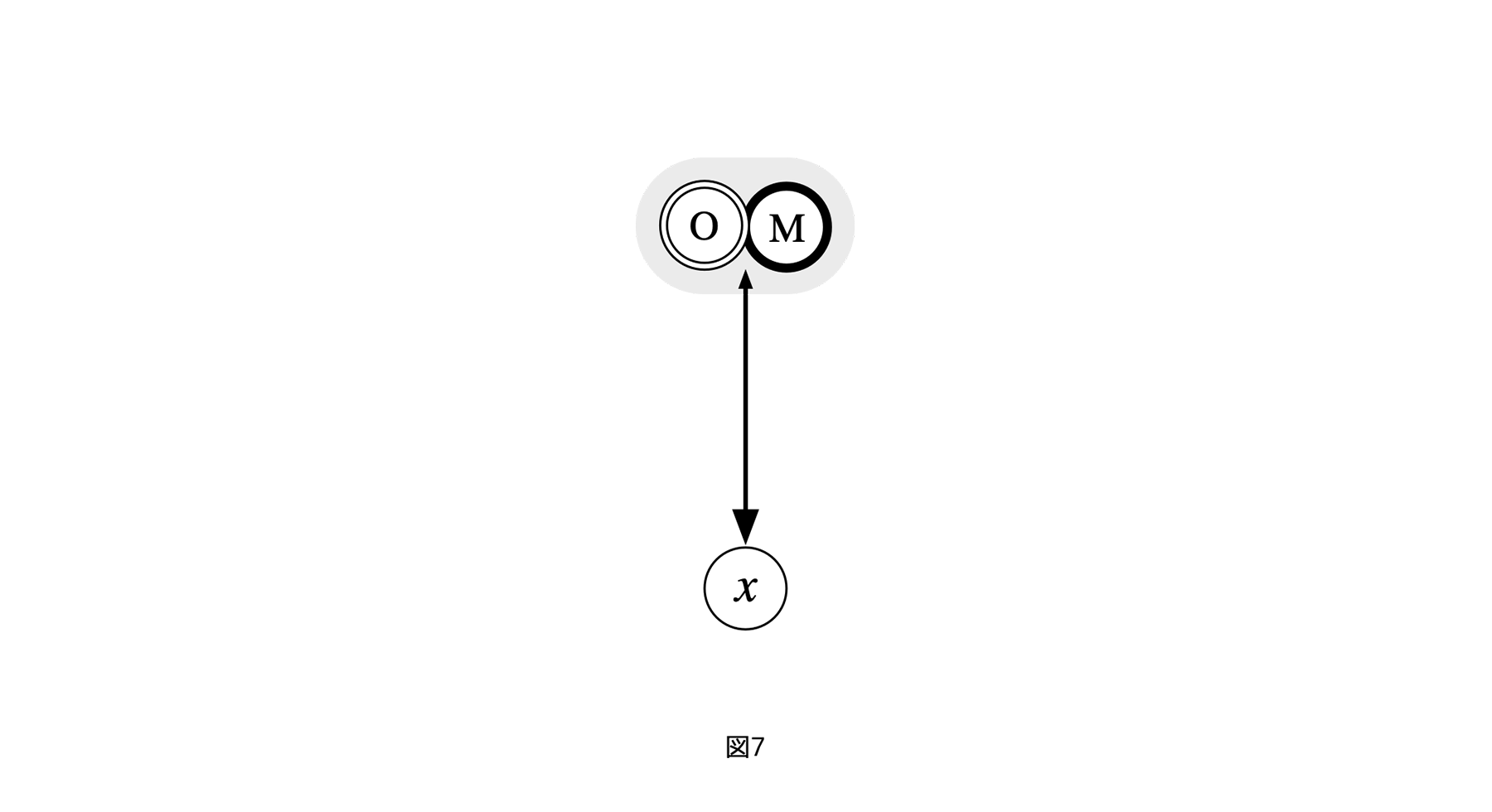［図7］
たとえば、図7のようにMOが結託し一体化すると、xに対するトップダウン構造が復活する。元々3つのレイヤーからなる構造なので、まだxからMやOへの制御も残る。だが、xからの制御はMとOという結託からの評価に対し、力が弱くなる。もちろん、この制御も前述のトップダウン評価が持つ難点を引き継ぐので望ましくない。
つまり、階層構造の欠点を克服するために、3レイヤーサイクルがあるが、制御者と制御対象の迎合・便宜という双方向化、それに起因するトップダウン制御への回帰が生じうる。このエッセイの目標は、この3レイヤーサイクルの難点を、可能な限り少ない変更、単純な構造で修正することだ。以下、まず、必要な概念と指針を方法論として準備する。その後、レイヤー数が3の場合からはじめ、レイヤー数や評価方法を増やし、その利点と難点を検討する。その結果、レイヤー数5が自然な要求を満たす最小のレイヤーとなるのが本稿の結論となる。
概念と指針
冒頭に述べた「フェアネス評価のターゲットが、評価者の利害関係からなるべく遠くなる」という指針は、次のように言い換えられる。
- なるべく自分のオブジェクトあるいはメタ・レイヤーから遠いレイヤー（＝利害関係者）が、「フェアネス評価」の対象になる構造を発見する
- 1の構造を「双方向制御」（および、それによる構造の破壊＝トップダウン化などの劣化）が生じないように維持する
以下、用語を定義し、これがなぜ、指針の言い換えになるのか説明する。
制御の双方向化、フェアネス評価、利害関係、メタ・フェアネス的課題
「制御の双方向化」とは、本来一方向であるべき制御が、先に述べた「迎合」や「便宜」のように、何らかの手段で双方向的になってしまったこと（癒着状態）だった。
先にも少し触れた「フェアネス評価」とは、あるレイヤーや、そのレイヤーによる他のレイヤーへの制御のあり方が、「色々な意味でフェア」であるか判定する評価である。たとえば、画家の描く絵を批評家がランク付けするとして、批評家の好む特定タイプの絵ばかり画家たちが描き始めたら迎合が起きている。それが公正な評価ではない、と指摘するのがフェアネス評価の一例だ。
あるレイヤーにとって、そのメタ・レイヤーやオブジェクト・レイヤーは直接の利害関係者なので、迎合・便宜を行うインセンティブが働きやすい。つまり、あるレイヤーがフェアネス評価を行うとき、そのレイヤーの直接の利害関係者がターゲットだと、フェアネス評価自体がアンフェアに操作されやすくなる。したがって、あるレイヤーのフェアネス評価の対象を、なるべく利害関係から遠くなるようにしたい。これが、権力分立構造デザインの第一目標になる。
なお、「色々な意味でフェア」と断るのは、《「フェアネス」の定義は様々であり、ここでは、その「「定義に依存しない（様々な種類の）フェアネス評価の運用」》で起きる問題を考えたいからだ。言い換えれば、フェアネス評価の矢印の内容は、「利害関係者を評価対象に含むと歪むようなタイプのフェアネス評価」なら、なんでも良い。
よって、ここで検討しているのは、「多様なフェアネスの定義が、ある構造に取り込まれた場合、そのフェアネスによる評価をフェアに運用しうるか？」という「メタ・フェアネス」的な課題だ。その最も近づきやすい素材として、3レイヤーサイクルを取り上げていると考えてもいい。
ちなみに、「フェアネス」という言葉、あるいは「正義」、「公正さ」という概念は、多くの場合運用の段階で、メタレベルから骨抜きにされ、現実主義的な観点から嘲笑される歴史を背負ってきた。しかし、フェアネスとその運用であるメタ・フェアネスは区別できるとするなら、両者を混同して捨て去る必然性はない。
本稿では、個別的なフェアネス定義が代入されうる場合を「フェアネス」、フェアネスの運用がフェアに行われうるかという検討をする場合を「メタ・フェアネス」と区別しておく。
フェアネス評価のターゲット
第二の指針は、フェアネス評価のターゲットに関わる。後述するが、フェアネス評価のターゲットは、「レイヤーそのもの」または「レイヤーによるレイヤーの制御（チャネル）」という2つの場合がある。
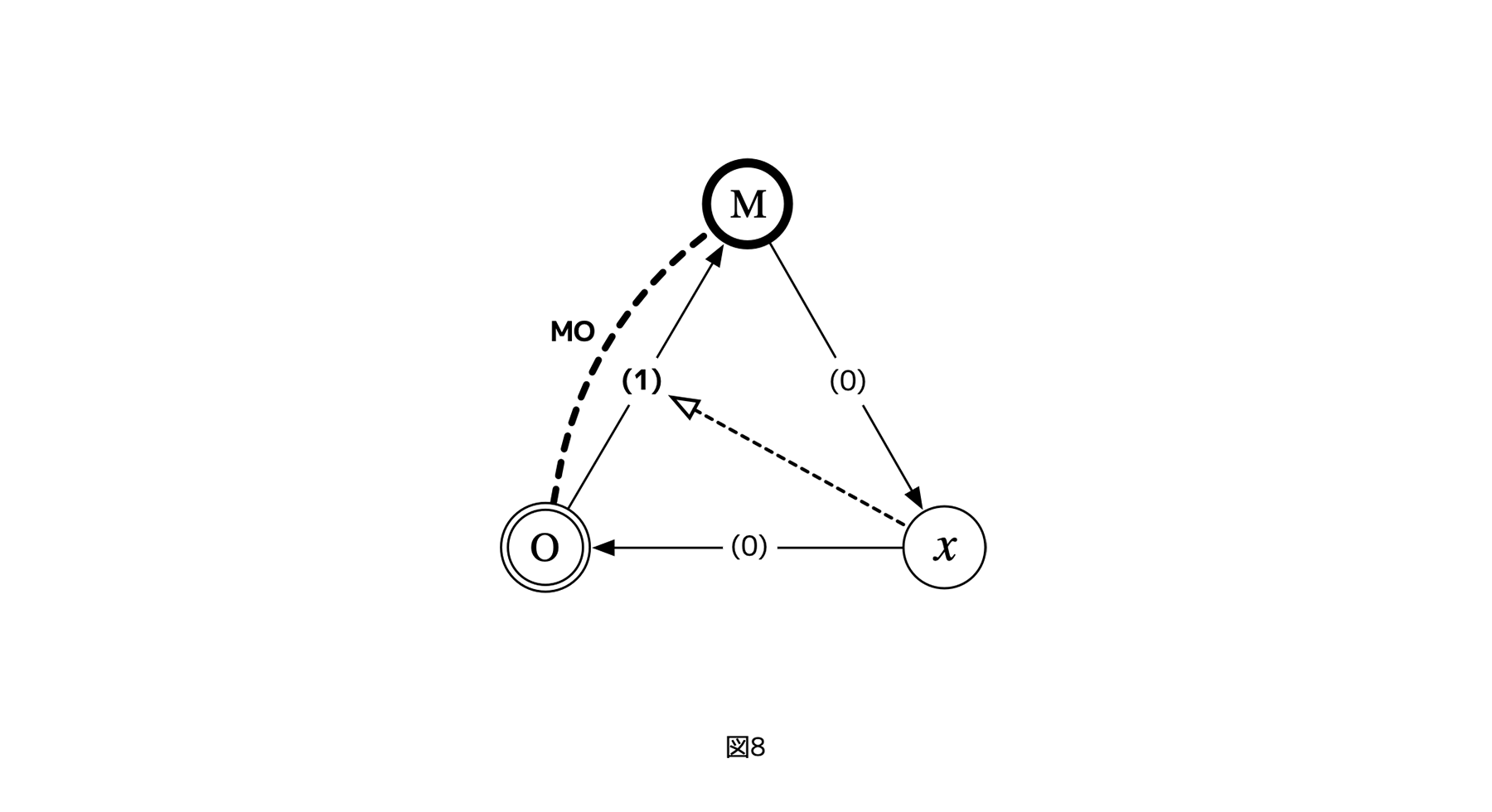［図8］
フェアネス評価は、たとえば図8のような状況で、チャネル(矢印)OMが一方向のままであり、迎合や便宜（まとめて癒着MO）で逆行していないかチェックする。先に述べた第一の指針と組み合わせると、「チャネルの一方向性を、なるべくそのチャネルの利害関係から遠いレイヤーが、フェアネス評価する」となる。
フェアネス評価が理想的に機能すると仮定すれば、3レイヤーサイクルは、（フェアネス評価によって全て解消されるので）双方向性によるトップダウン化が起きず、分権を存続できる。しかし、上図でフェアネス評価を行う評価者x自体が、Mに評価される利害関係者であることを無視できるだろうか？
利害関係ランクと評価構造
ここで、利害関係や利害関係者の「遠さ」を、もう少しはっきり定義しよう。まず、利害関係を考える基準として仮に選ぶ参照レイヤーxを決める。このxに直結してxを制御するメタ・レイヤーMや、逆にxに評価されるオブジェクト・レイヤーOを、「（xからみた）ランク1の利害レイヤー」と呼ぶことにしよう。xを制御したり、xに制御されたりということで、MやOは、常識的な意味での「x利害関係者」そのものである。
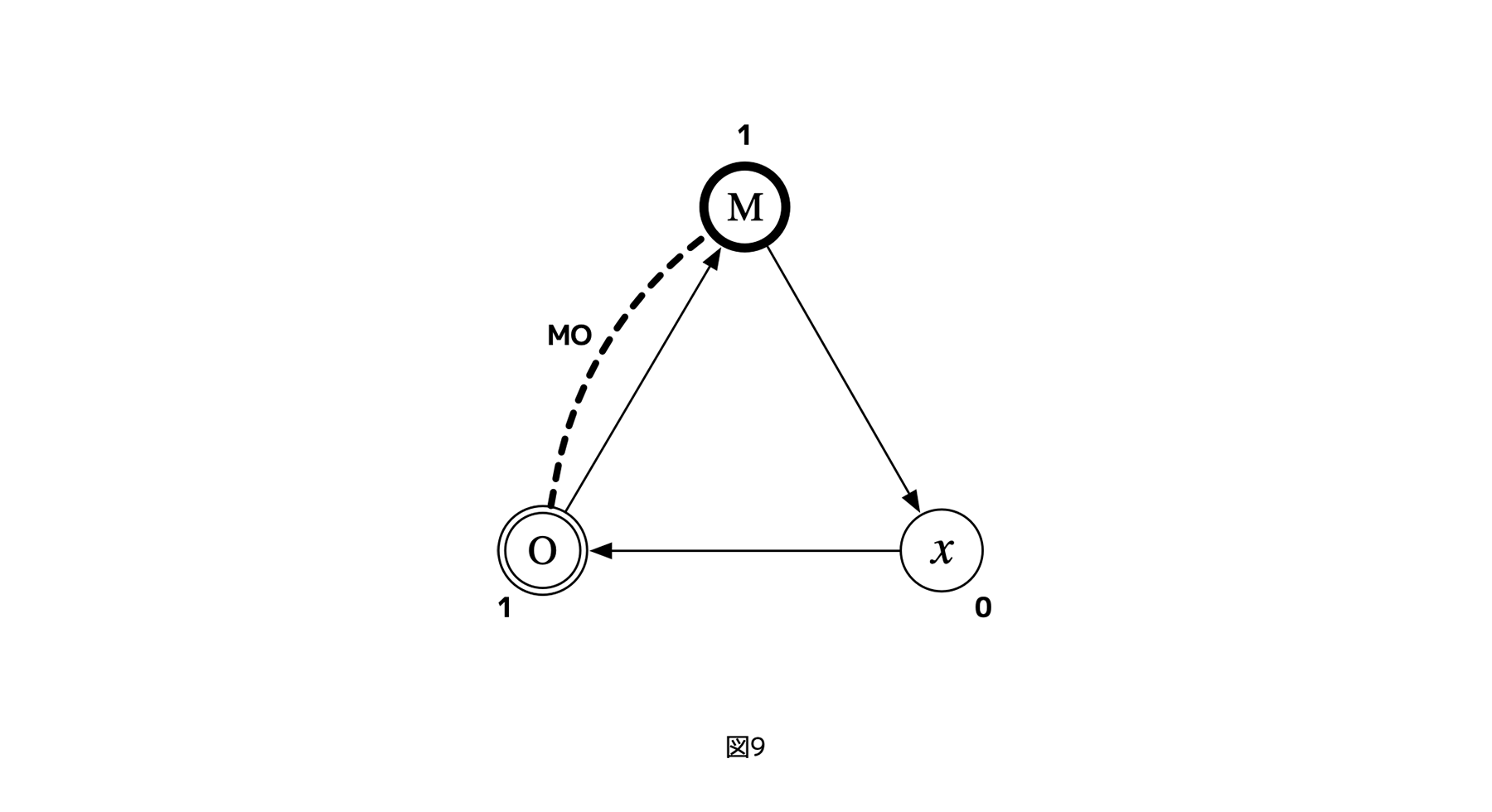［図9］MとOはランク1の利害レイヤー
次に、レイヤーからレイヤーへの制御であるチャネル(矢印)に対しても、ランクを定義したい。フェアネス評価は、利害関係に対しても行われるからだ。ここでは「チャネルの起点または終点になる利害アクターの最も低いランク」を、その制御＝チャネルのランク、つまり「利害関係」のランクとする。たとえば、3レイヤーサイクルで「（xからみた）ランク1の利害関係」は、OからMへの制御関係（チャネルOM）となる。なぜなら、定義に従うとチャネルOMの起点または終点になる利害レイヤーMとOは、ともに、xからみて、ランク1の利害レイヤーである。そして、MとOの中で最も低いランクは1である。よってチャネルOMのランクは1となるからだ。なお、「最も低い」ランクを選ぶ理由は後述する。
図10のグレーの網点で囲まれた集合（M、O、チャネルOM）が、xからみたランク1の利害レイヤー／利害関係である。なお、癒着である便宜MOは、ランク1の利害関係OMに付随して現れる現象（OMの反転としてのMO）だが、これもランク1の利害関係に含めて扱う。
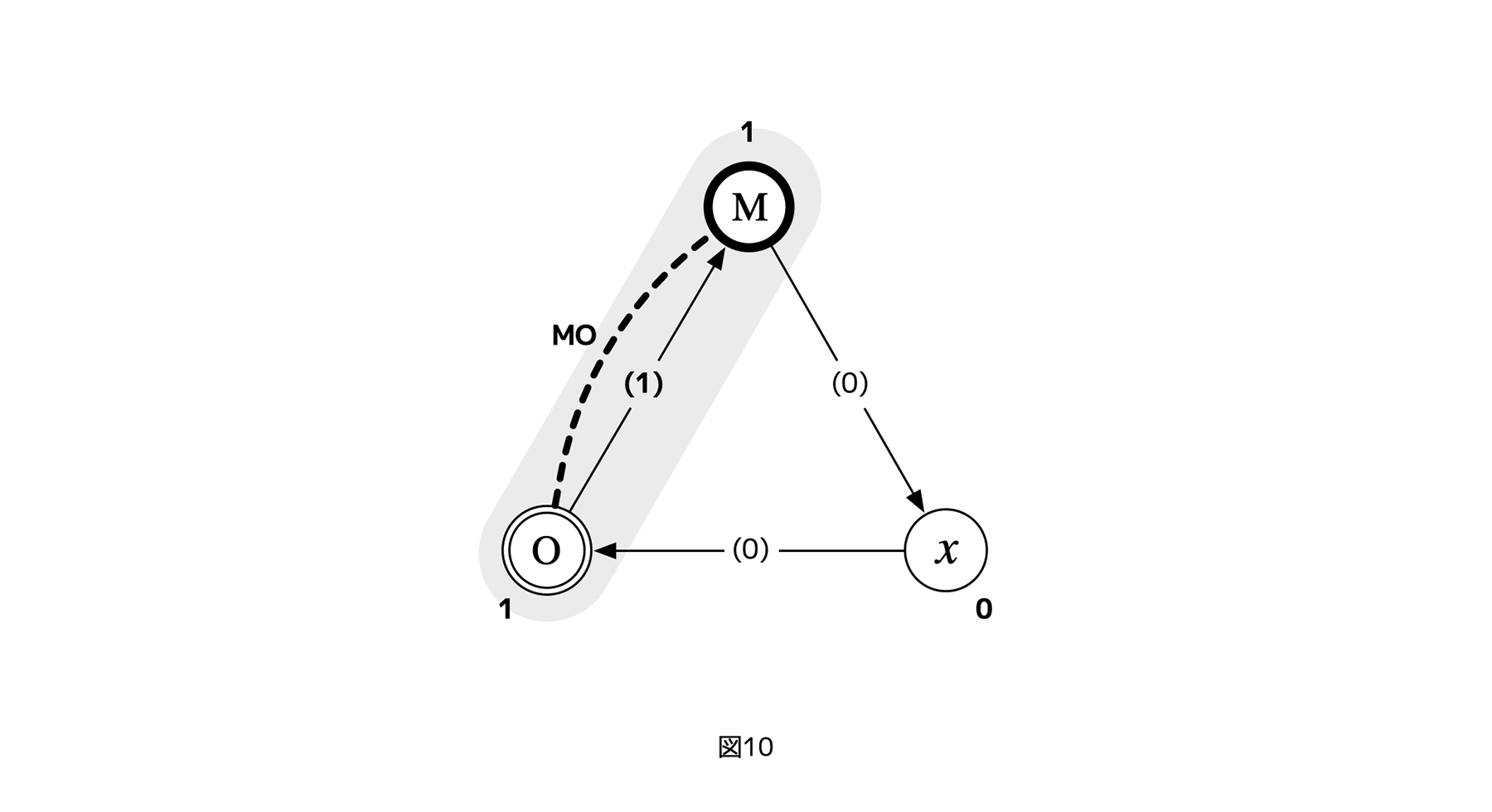［図10］
なお、もしx自身を「（xからみた）ランク0の利害レイヤー」とすれば、オブジェクトおよびメタのレイヤーとxをつなぐ矢印(チャネル)MxやxOは、「ランク0の利害関係」となる。これらの矢印(チャネル)（MxやxO）が、ランク1の利害レイヤー（M,O）とランク0の利害レイヤーxを含む。そのため、最低ランクの0が、MxやxOのxからみたランクになるからだ。ここでは矢印(チャネル)の起点と終点で利害レイヤーのランクが異なる。ゆえに、（1, 0という2つのランクから）最低のランクを選ぶ必要性がある。
以下、不要な場合「xからみた」は適時省略する。省略が可能なのは、図形の構造上、「xをどこに定めても利害関係に影響が出ない」という対称性が保たれているからだが、人間にとってはどこかに基準を定めた方が分かりやすいので補う場合もある。
フェアネス評価と利害レイヤー／利害関係のランク、あるいは、メタ・フェアネス強度で表現された指針
「フェアネスの評価を行うターゲットが、評価者の利害関係からなるべく遠くなる」という指針を、ここまでに定義した概念で少しリファインしてみよう。
指針1. （図式内に存在する）任意のレイヤーxにとって「（xからみた）利害関係ランク」が、なるべく高い（＝遠い）制御、もしくは、「（xからみた）利害レイヤーランク」がなるべく高いレイヤー、を「レイヤーxからみたフェアネス評価のターゲット」にする
指針2. 指針1の、「フェアネス評価ターゲットランク」が、参照レイヤー（たとえばx）の取り方に依存しない
指針3. 構造変化、あるいは実運用によって、新たな制御や評価の双方向化が導出されない
・・・となるだろう。ただし、指針1のままだと「なるべく高い」の基準がないので、ここでは
指針1′. フェアネス評価ターゲットを、「ランク2以上」の利害関係または利害レイヤーにする
・・・と具体化する。また指針1、指針2に現れる「あるレイヤーxを参照としたフェアネス評価ターゲットの最小ランク」を簡単のため「xのフェアネス強度」と呼んでおく。なお、「強度」と言っているのは、ｘがフェアネスを損なうことなくフェアネス評価を行える限界を決める量につけた名前だからだ（また、この量がグラフの部分とその数によって決まる外延量ではなく、分割すると変化する全体構造に依存した量で、（カント的な意味での）強度量だからという意図もある）。
指針3.は「フェアネス評価やレイヤーの追加による権力分立のグラフ構造変動や、権力分立構造の実運用が、新たに（元々存在しなかった）双方向評価を生み出してしまわない」という意味だ。具体例は後述する。
以下、この指針に従い、様々なレイヤー数の構造や、フェアネス評価のターゲットについて検討する。その際、
指針+ なるべくレイヤー数、評価数が少ない構造で、指針を満たす
・・・という前提も置く。主に計算や認識などのコストから、「少ない方がいい」という理由だが、自明ではない。これらのコストが大きく下がったので、レイヤー数はいくらあってもいいから、フェアネス強度を恐ろしく高めたい、という事態が起きても不思議はないからだ。ただし、本稿では、その方向性は追及しない。
なお、グラフ中の様々なレイヤーを参照したとき、上記指針を満たす「最小の」フェアネス強度は、図式の持つグラフ構造によって決まる内在的、トポロジー的属性である。この量をそのグラフの「メタ・フェアネス強度」と呼ぶことにする。「最小」を選ぶ理由は次の通り。たとえば、あるレイヤーxのフェアネス強度が2だとして、別のレイヤーyのフェアネス強度が（図式の構造上）どうしても1になるとする。このとき、そのグラフ全体のメタ・フェアネス強度は、1と考える必要がある。なぜならこれは、グラフ全体としては、最もフェアネス強度が低いところから癒着が始まるとするのが自然であるためだ。
ただし、指針2が満たされている場合、フェアネス強度は、参照レイヤーのとり方に依存しないので、「最小の」という条件は自動的に満たされ、この点を気にする必要はない（本稿では、基本的に指針2が満たされたグラフ構造を扱っているが、何らかの非対称性が入っていた方が、同じ指針に基づいて優れている可能性は十分ある）。
また、上の定義で「メタ」という接頭辞がつくのは、「メタ・フェアネス強度」が、個別的で多様なフェアネス定義たちではなく、（「フェアネス」の内容はなんであれ）フェアネス評価を実行するときのグラフ構造だけで決まる一階上の構造だからだ。それは「そのフェアネス定義による評価自体がフェアに運用される構造はありうるか？」という問いへの答えになる。たとえば、通常の三権分立は、以前の原稿※5の定義では2レイヤー構造を持つが、それはそのままでは運用が難しい。
よって、我々の問題は、
問題+ メタ・ フェアネス強度2以上を達成する、最小レイヤー数の（対称な）グラフ構造を見つけること
と言い換えることもできる。
指針からみたレイヤー数の検討
論旨を見失わないために、結論を先取りしておくと「指針を全て満たす最小レイヤー数は5である」というのが本稿の結論になる。レイヤー数3、4では
+ ランク1利害レイヤーを、フェアネス評価ターゲットに含めない
+ フェアネス評価の追加が、新たな双方向制御を導出しない
・・・の両方を同時に満たすようにできず、メタ・フェアネス強度2以上を達成できないからだ。
以下、3レイヤーサイクルにフェアネス評価を導入したケースからはじめ、次にレイヤー数に応じた利点・難点について述べる。その後、図式の修正を指針に沿って行っていくと、レイヤー数は最小で5つ必要になる。結論であるレイヤー数5の5レイヤーサイクルだけを検討しないのは、他の図式にも利点があることと、他の図式の難点を経由しないと、適切なレイヤー数の最小値が5であるとここで考える理由の説明が難しくなるためである。
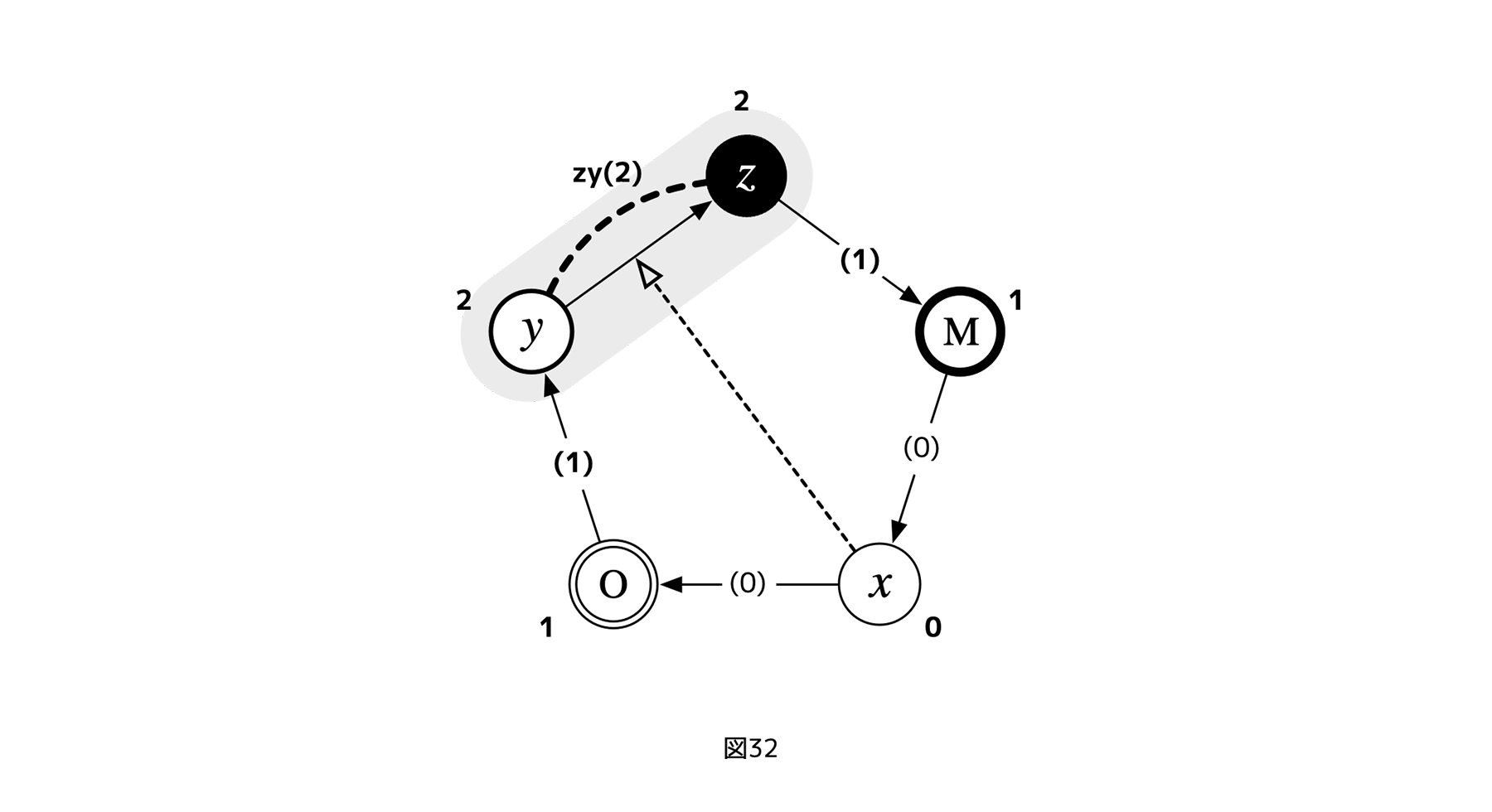
3レイヤーの場合
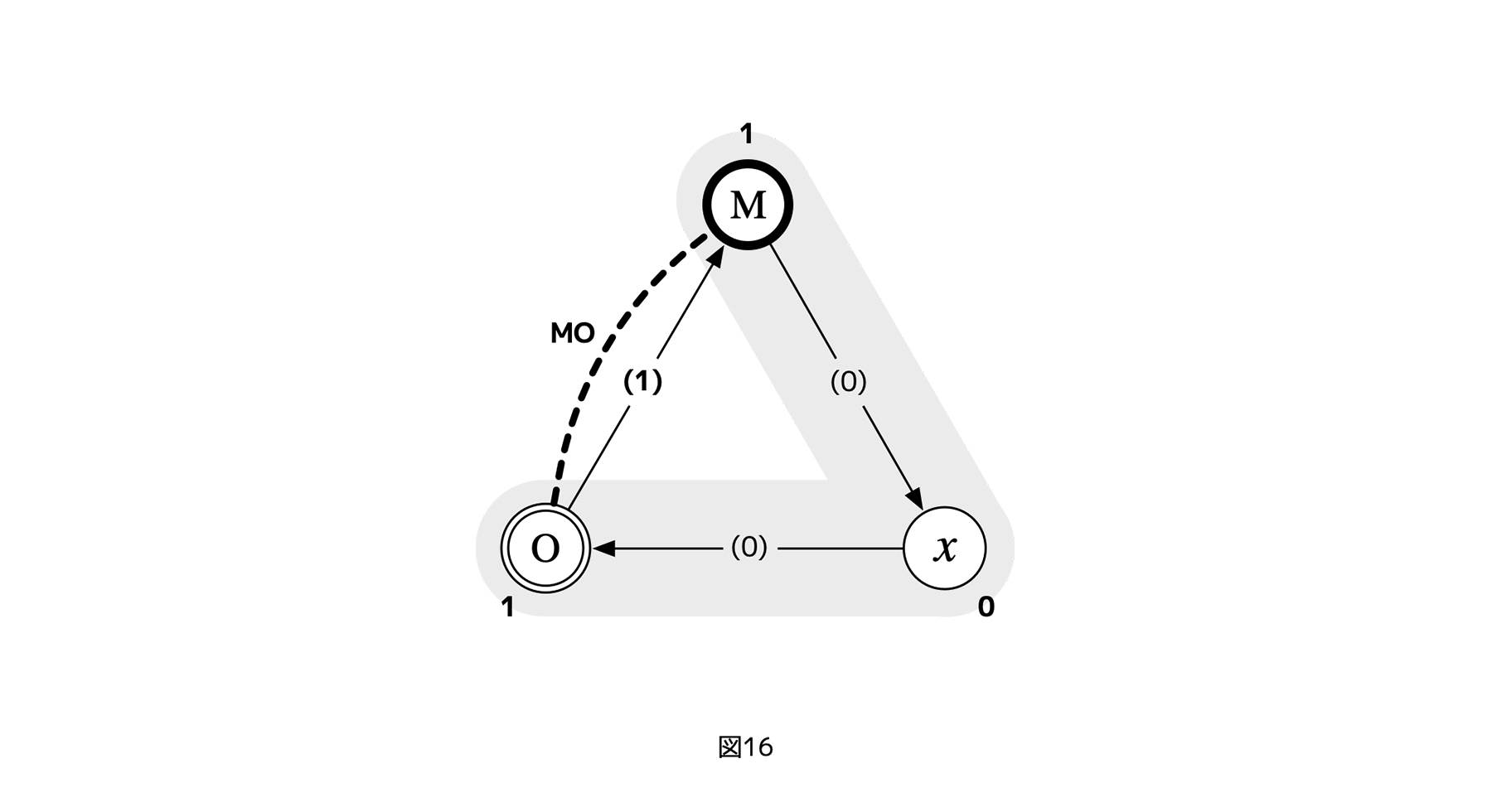
まず、3レイヤーサイクルにランク1利害関係をターゲットとしたフェアネス評価を入れた図式を考える。利害関係からできるだけ離れるという指針より、フェアネス評価は、利害レイヤー以外を起点にする必要がある。だから、たとえば、OMという制御を対象にしたフェアネス評価を行うことができるのは、M,O以外のレイヤー、つまりxだけである。つまり、3レイヤーサイクルの場合、フェアネス評価の入れ方は一つしかない。
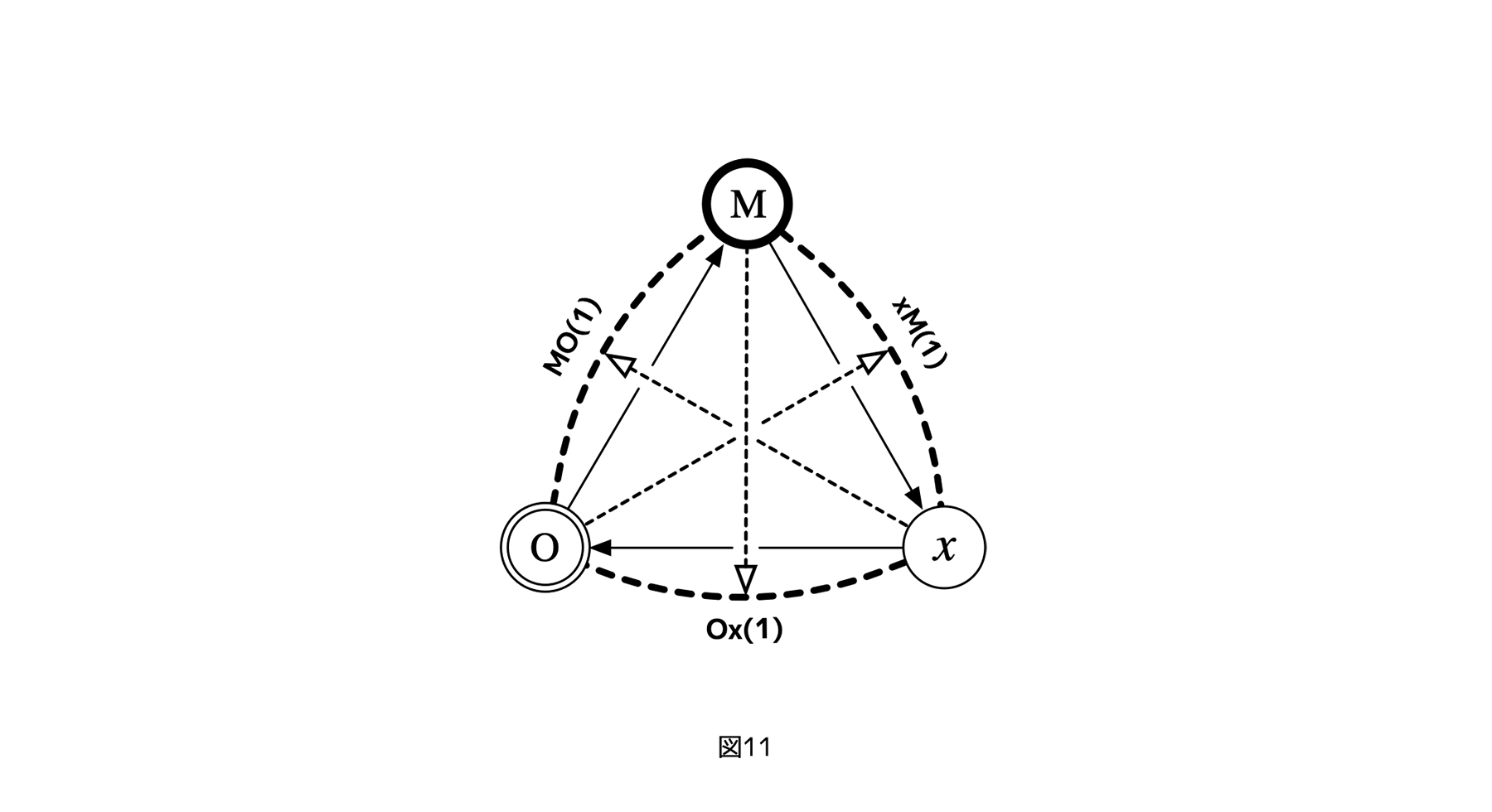［図11］
よって、そのときの構造は、図11のように描ける。点線で示した矢印M-Ox(1)、x-MO(1)、O-xM(1)が、それぞれ、Mから制御xOへのフェアネス評価、xからOM、OからMxに対するそれを表す（括弧内は、フェアネス評価の起点となるレイヤーを参照レイヤーとした場合の利害関係のランク数）。なお、ここでたとえば、制御xOに対するフェアネスの記号をOxなどと逆転するのは、フェアネス評価が、制御方向の逆転をチェックするものであるという性質を強調するためだ。
これらのフェアネス評価矢印は、上図では三角形内部を通過するように描かれ、一見交差しているように見える。しかし、実際は、この図が埋め込まれている平面には意味がないので、下図のように三角形外側を廻るように描いても同じ図式を表現している。つまり、図12、図13は同じ状況を表現するが、以後は簡便のため、図11、または図12のように描く。
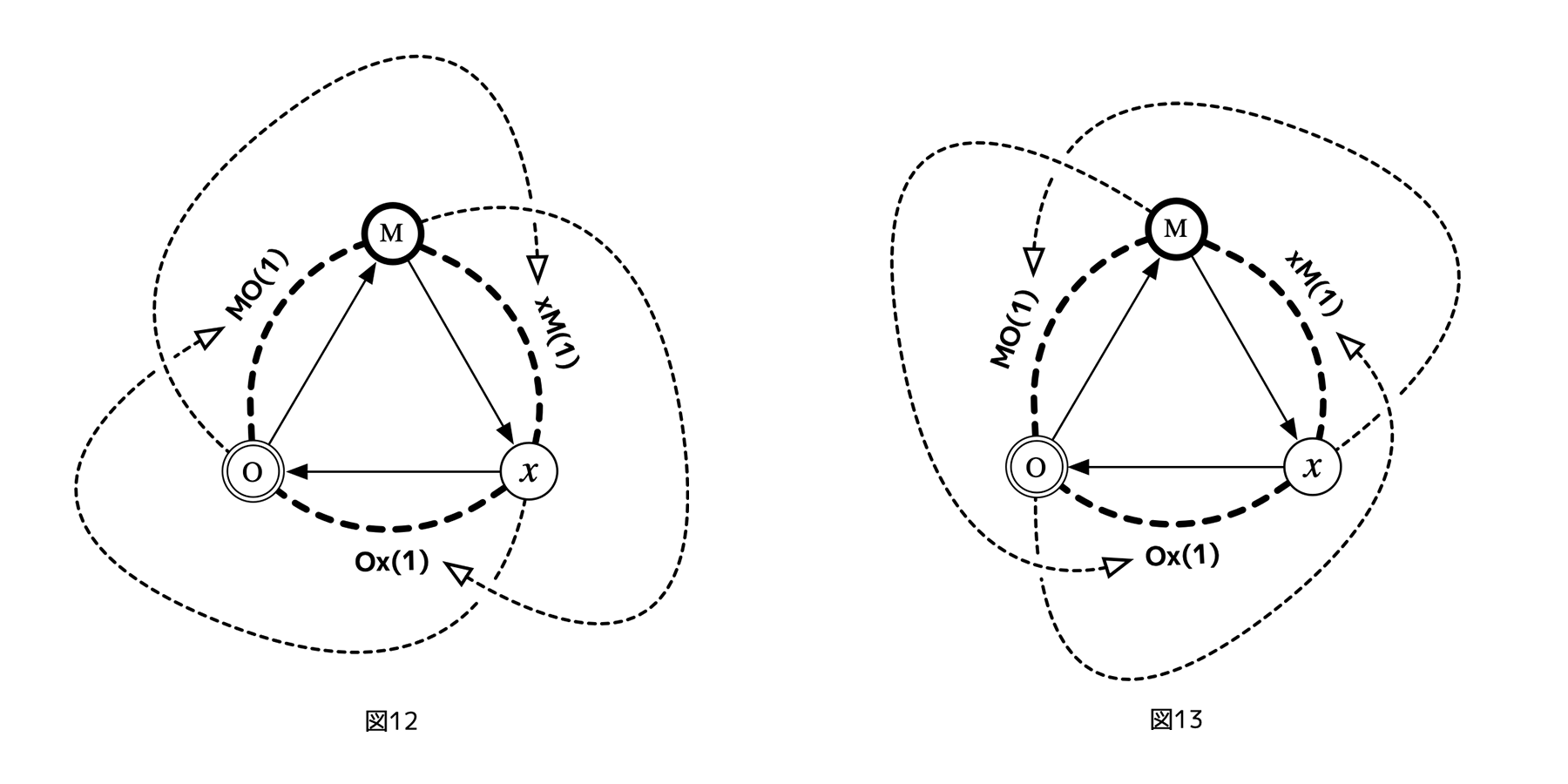［図12］［図13］
つまり、3つの図は同じ図式を表現しているが、最初の図に存在する三角形の重心が特に意味を持たないことを示すために下の2つの図を載せている（なお右図においてチャネルへ向かうフェアネス評価の矢印が左図とは逆の方向に旋回しているが、当然、矢印の向きが時計まわり反時計回りのどちらでも意味は変わらない）。
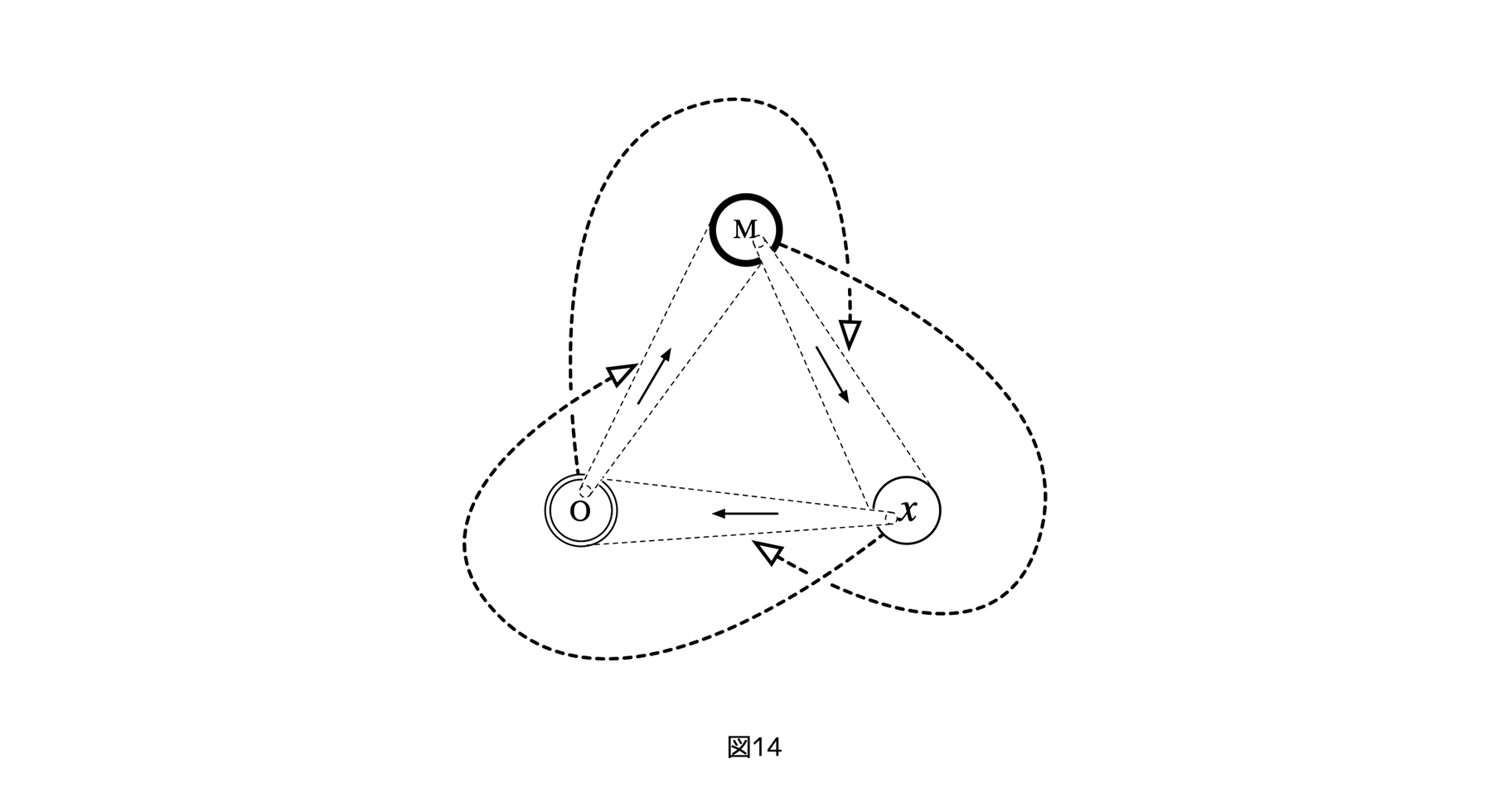［図14］
また、4つめの図14は、先の図4に対応するもので、階層の概念を図の表記に反映させた場合、レイヤー、メタ・レイヤー、オブジェクト・レイヤーが相互に入れ子になっていることを示す。他の図では、簡単にするため、このような入れ子関係はみえなくなっていることに注意されたい。
なお、我々が入れ子関係に注意をうながすのは、このような相互入れ子構造自体は、多くの分野でみられること、逆に、それにフェアネス評価のような矢印がついた構造はあまりみられないことが興味深いからであり、同時にそれが「アクター」などの行為者を表す概念ではなく、「レイヤー」という同一のフレームに重ね合わされる概念を使う理由でもあるからだ。
その点を再確認するため、ここに前にみた、フレームとして重ね合わせになった3レイヤーサイクルの図5にフェアネス評価の入った図15を載せておく。
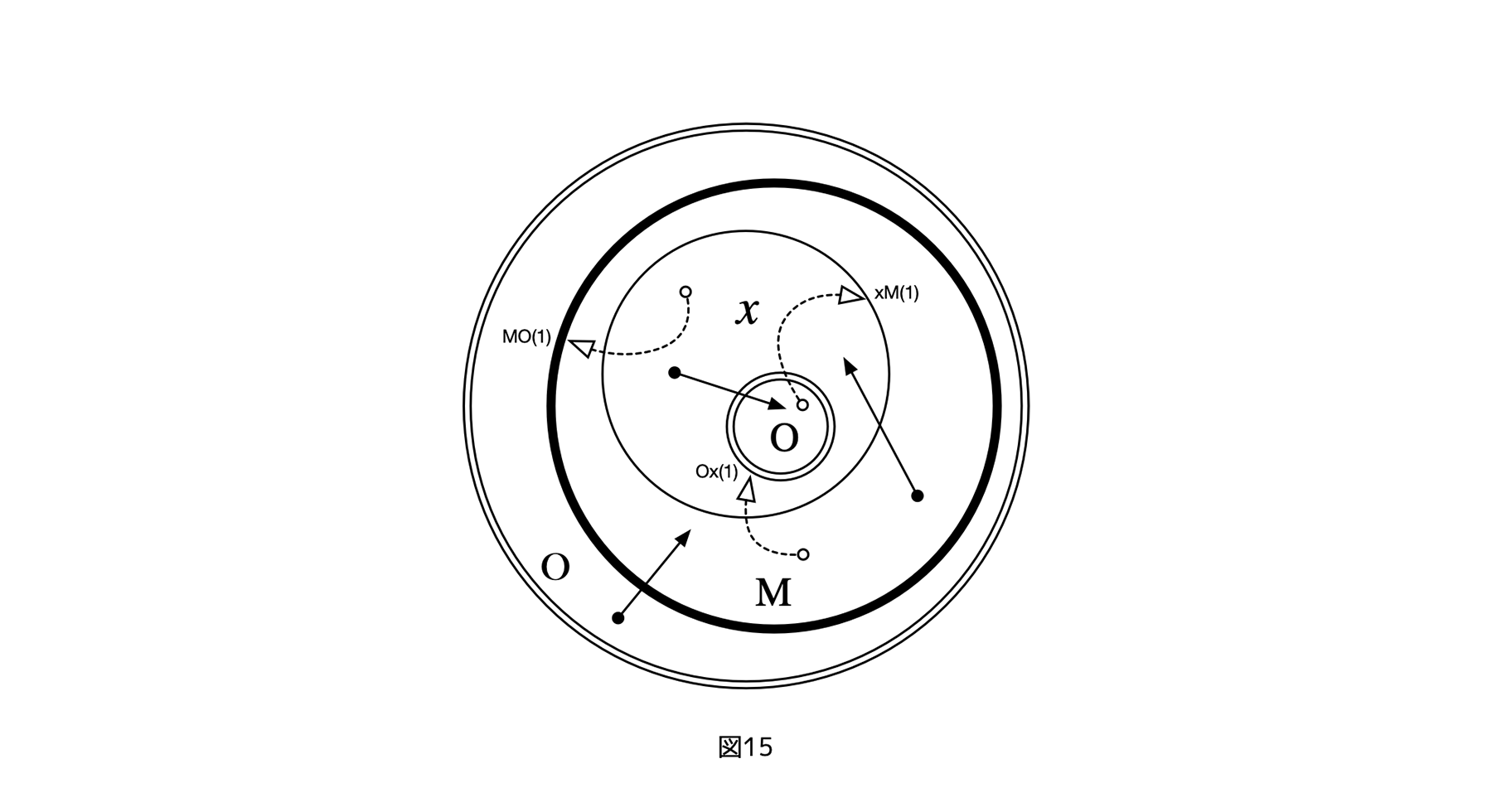［図15］
この「3レイヤーサイクル」でフェアネス評価が正常に機能すると仮定する。すると、もし、3レイヤーサイクルに癒着が発生し、一箇所が双方向制御になりかけたとしても、それを癒着に無関係な第三者のレイヤーがチェックすることで補正できる。たとえば制御OMに癒着が発生しかけても、xからのフェアネス評価x-MO(1)が正常に機能すれば、先に見たような（結託したMとOに一方的にxが制御されるという）トップダウン構造が固着化する前に、3レイヤーサイクルに戻すことができる。
3レイヤーでのフェアネス評価の難点
しかし、このような構造のフェアネス評価を追加しても、三つしかレイヤーがない場合、
+ フェアネス評価ターゲットとなる利害関係（図16でMO）が、その利害関係の起点または終点（MまたはO）に、フェアネス評価の起点となるレイヤーx自身の、メタ・レイヤーM、オブジェクト・レイヤーO（共にxにとってのランク1の利害アクター）が含まれないようにできない（xから始まる網掛け範囲にMやOが入ってしまう）。
［図16］
・・・という難点が残る。換言すれば、3レイヤーサイクルのメタ・フェアネス強度は1である。
つまり、あるレイヤーにとって、メタ・レイヤー、オブジェクト・レイヤーは両方とも自分の直接的利害関係者（ランク1利害レイヤー）なので、フェアネス評価する際にどちらかに有利な評価をするインセンティブが生まれてしまう。ちなみに、両方を考慮に入れて二股をかけるというのは、古典的な他者の操縦方法である。そして、両者を天秤にかけた結果、有利な方と結託すれば、3レイヤーサイクルがトップダウン制御に変わるので、不安定である。
3レイヤーサイクルの利点
以上の難点を踏まえた上で、再度3レイヤーサイクルを評価してみる。
3レイヤーサイクルには、
+ フェアネス評価を導入できる最小のレイヤー数
+ レイヤー間の利害関係が解釈しやすく、動作が単純
・・・という利点がある。
フェアネス評価によって図式がトップダウン型に潰れるのを防ぎ続けるというアイデア自体は、3レイヤーサイクルの段階でも説明可能だし、意味を持つ。また、3レイヤーサイクルは4レイヤーや5レイヤーなどの図式を考える際、ミニマムなモデルとして今後も利用できる。
レイヤー数の少なさは重要なファクターである。なぜならば、レイヤー数3と4の違いが認知や計算にもたらす複雑さの増加は累乗的なものになる可能性があるからだ。レイヤーの増加は、「レイヤーが一つ増える」という語感よりもはるかに大きなコストを伴う。つまり、各レイヤー内にいるメンバー数（レイヤーは基本的に多数のアクターから構成されるグループを想定していたのを思い出してほしい）や選択肢など、本来の計算量の基準をNとすると、二者関係ならO(N2)、三者関係や四者関係はO(N3)、O(N4)という計算コストになっていくという言い方もできる。また、人間が権力分立構造を解釈するとき、3より増やしていける数はそう多くはない、というもの、あなたが人間なら納得していただけるだろう。
4レイヤーの場合
3レイヤーサイクルの難点は、3というレイヤー数に由来する。そこで、レイヤーを一枚増やしての解決を模索してみよう。
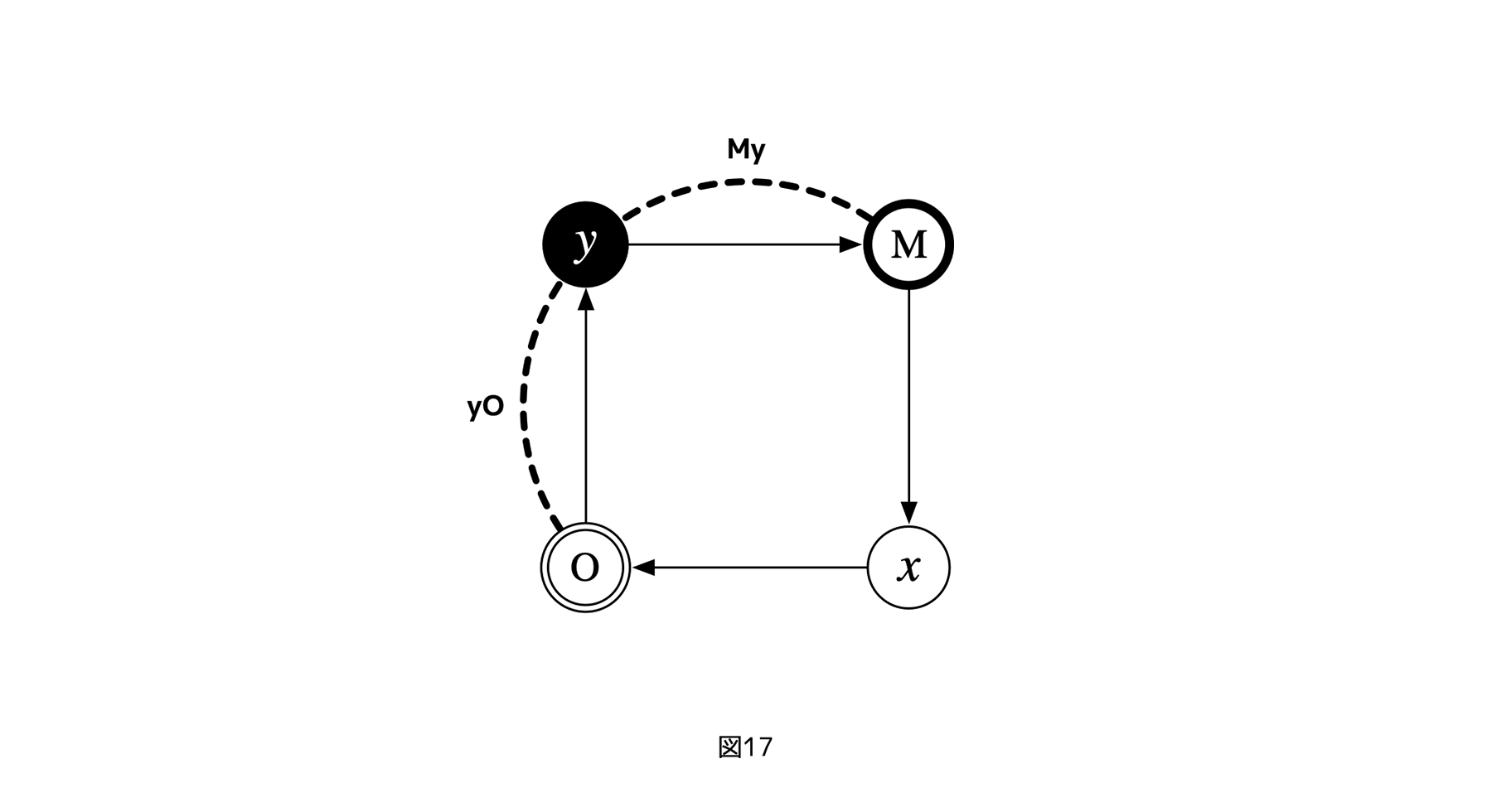
図17は、3レイヤーサイクルに新しいレイヤーyを追加したものであり、新しい利害関係My、yOが付随して現れる。以下この図式とフェアネス評価の関係について議論する。
［図17］
4層以上のレイヤー数の場合、フェアネス評価のターゲットは2つの場合がある。それぞれの利点があるので、別々に検討する。
4レイヤーサイクル
まず、フェアネス評価のターゲットが（レイヤー間の利害関係の評価ではなく）レイヤーそのものである場合を考える。
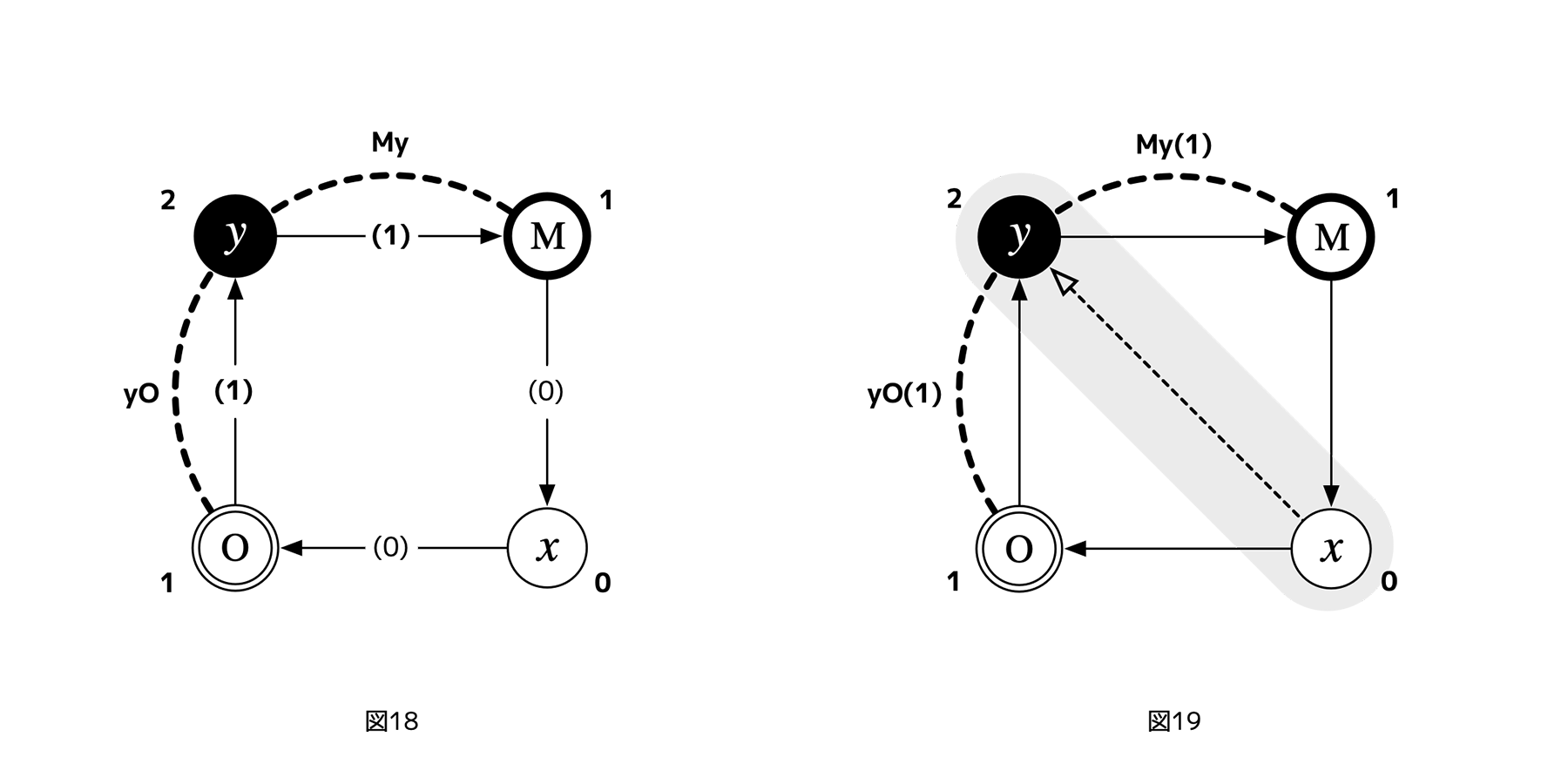
仮にxを参照レイヤーとすると、xにとってのランク2の利害レイヤーであるyが、（xから最も遠い利害レイヤーなので、指針に従い）xからのフェアネス評価ターゲットになる。図18は、xからみた（レイヤー、関係の）利害ランク、図19はxからyへのフェアネス評価を追加した図である。
［図18］［図19］
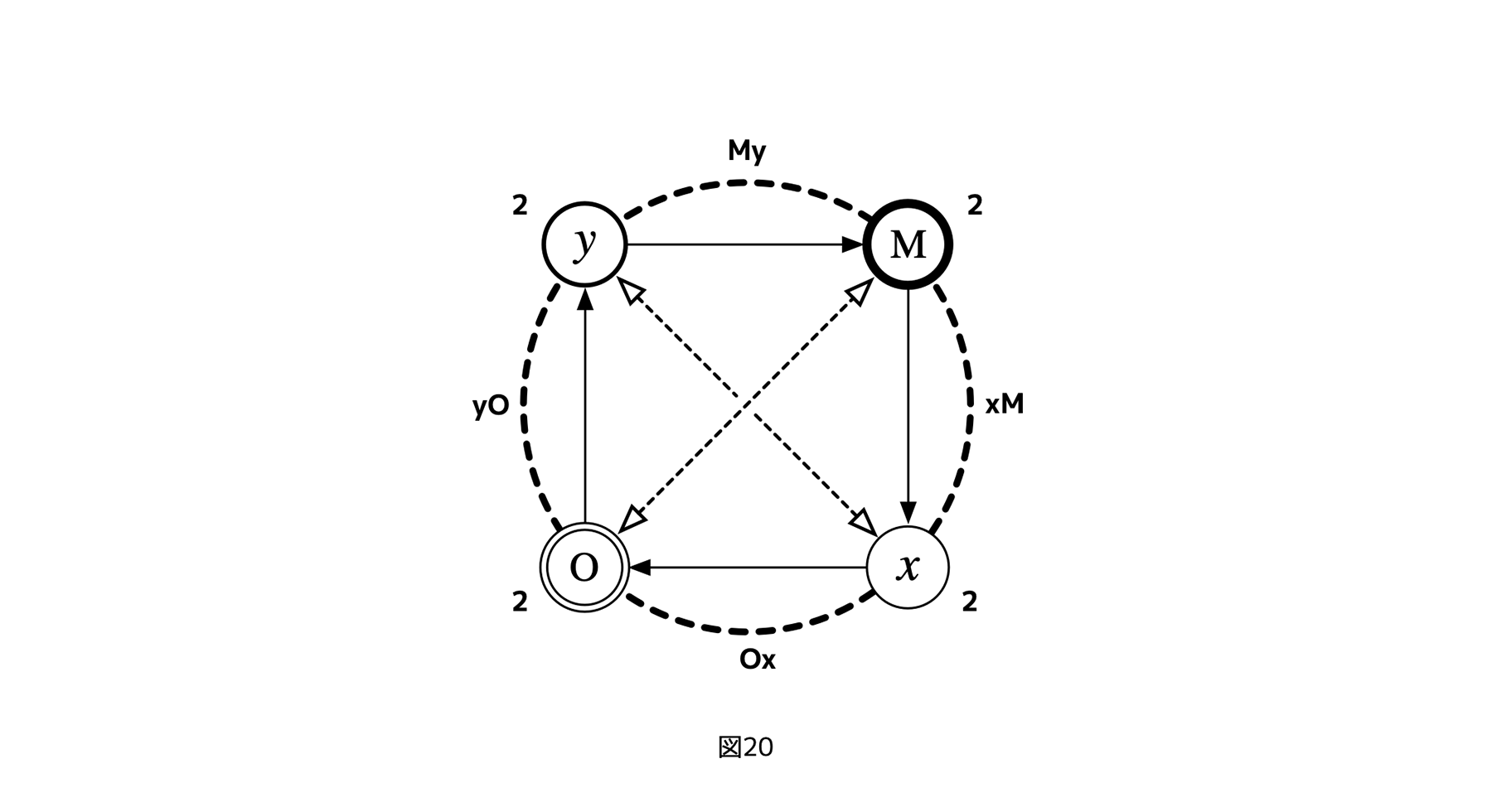
この場合、xが対角線上のレイヤーであるyを評価するので、この図式を「対角4レイヤーサイクル」と呼ぼう。この方針で、全てのレイヤーからのフェアネス評価矢印を追加すると、図20のようになる。
［図20］
対角4レイヤーサイクルに至ったことで、初めて
+ xを起点とするフェアネス評価のターゲットが、ランク1の利害（＝ランク1の利害レイヤーM、O、ランク1の利害関係My、yOおよびその逆）を含まない
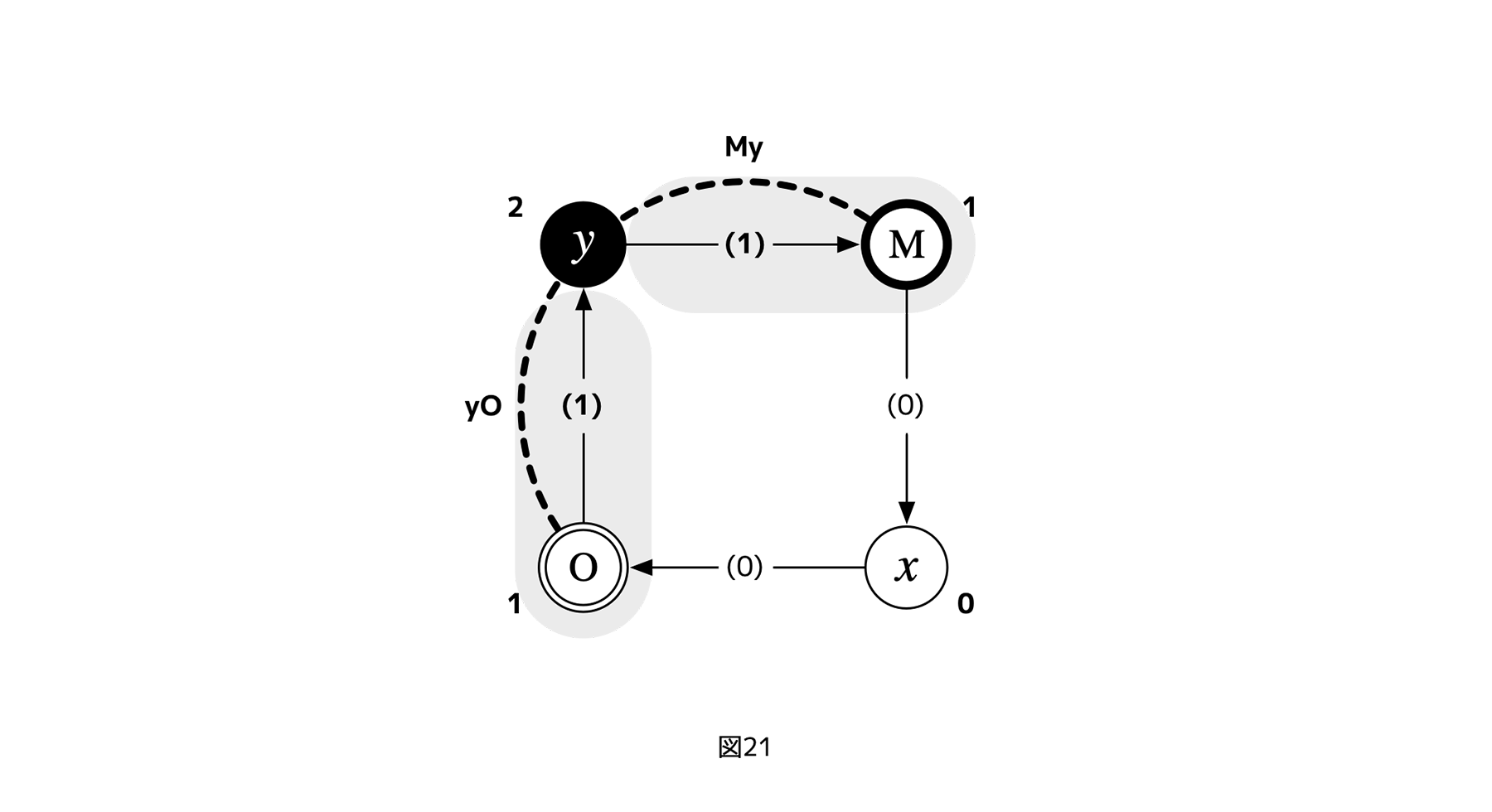［図21］
・・・という状態にできる。なお、「利害関係のランク」は、ある関係、たとえばMyに含まれる利害レイヤーの最低ランクだったことを思い出してほしい。この場合、Myに含まれるyのランクは2、Mは1なので、結果Myという関係のランクは（xからみて）1となる（図21の網掛け部参照）。
3レイヤーサイクルでは（ランク2の利害レイヤー＝yが存在しないので）図形上不可能だったが、四項にすることでフェアネス評価対象の利害ランクを2以上にし、xの直接的（＝ランク1の）利害レイヤーおよび利害関係を、xのフェアネス評価対象から外すことができる。また、レイヤー間の関係では無く、レイヤーをフェアネス評価の対象とする対角4レイヤーサイクルには、認知的にも計算量的にも難しい「制御の評価」をフェアネス評価とせず、しかも、3レイヤーサイクルの難点であるランク1利害関係に関与するフェアネス評価を無くせるという利点もある。
対角4レイヤーサイクルの難点
しかし、4グループのレイヤー達に対し、対角線は二本しかないので、図20のようにフェアネス評価自体が双方向評価にならざるを得ない。つまり、指針を満たすようにランク2の利害レイヤーをターゲットにするなら、xはy、yはxをフェアネス評価のターゲットにするしかない。M、Oのペアについても同様である。よって、対角4レイヤーサイクルは、フェアネス評価が、新たに避けるべきだった「フェアネス評価同士の双方向評価」を導出してしまう。だから、双方向評価を禁止する方針に矛盾してしまう。
非対角4レイヤーサイクル：利害関係をターゲットとしたフェアネス評価による双方向化の回避
対角4レイヤーサイクルで導出されてしまう双方向評価を避けるため、フェアネス評価のターゲットを利害レイヤーから利害関係に戻してみる。
この場合、xからyに至る経路が2つあることに呼応して、
+ レイヤーxは、自分のオブジェクト・レイヤーOのオブジェクトにあたるレイヤーyへの制御Oyをフェアネス評価する
または、
+ レイヤーxは、自分のメタ・レイヤーMのメタにあたるレイヤーyからの制御yMをフェアネス評価する
という図式［図22］になる（チャネル(矢印)に描かれた数字は、参照レイヤーをxとした場合の利害ランク。利害関係なので、先の「利害関係ランク」に対する定義に従いランク2のyではなく、ランク1のMのランクが、関係自身のランクになることに注意＝網掛け部分）。
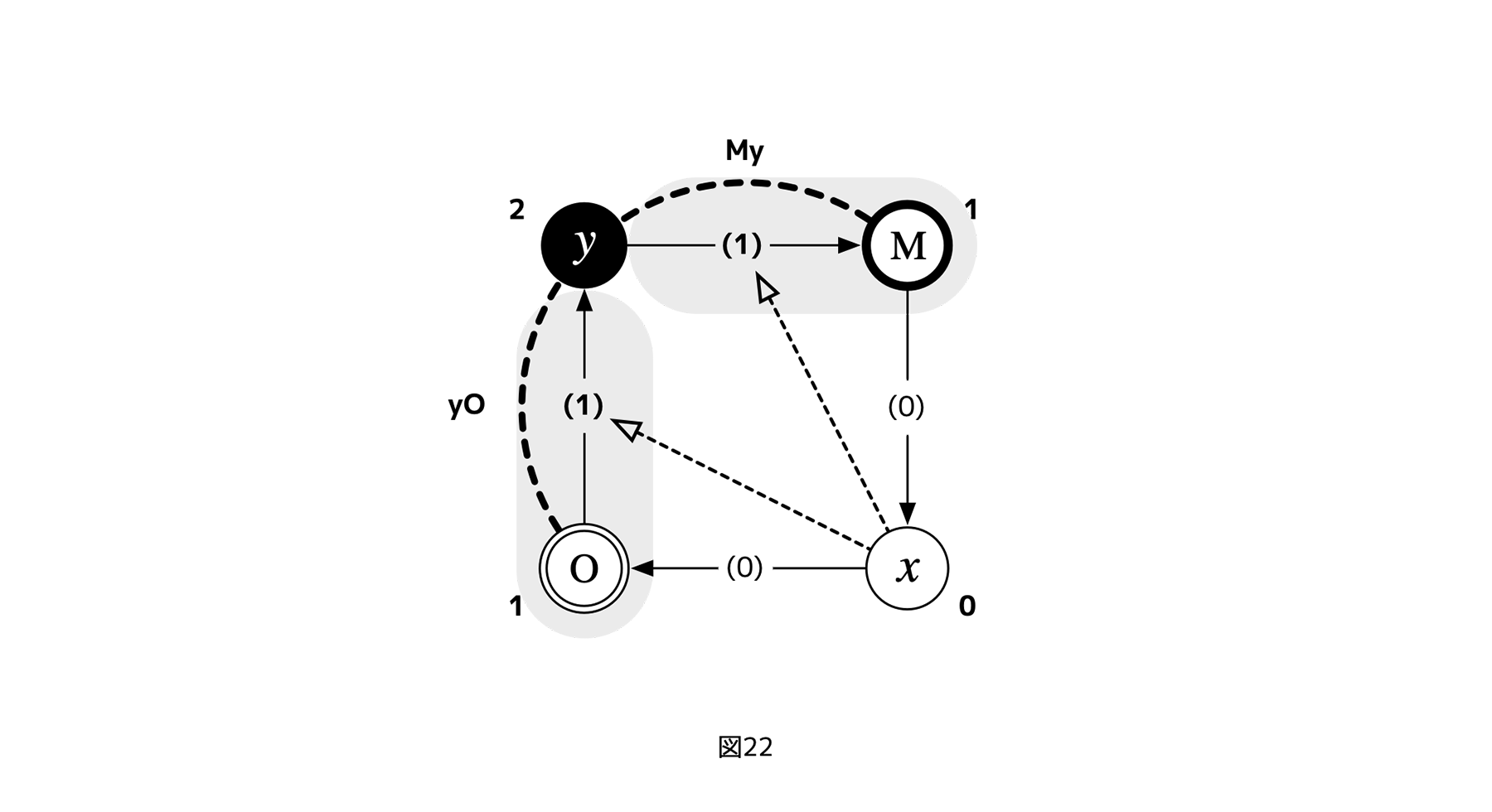［図22］
こうすると、どちらの場合でも、フェアネス評価が3レイヤーサイクルと同様に「制御の評価」を意味し解釈が難しくなってしまうが、かわりに、図23、図24のように、
+ すべてのフェアネス評価はターゲットを共有しない
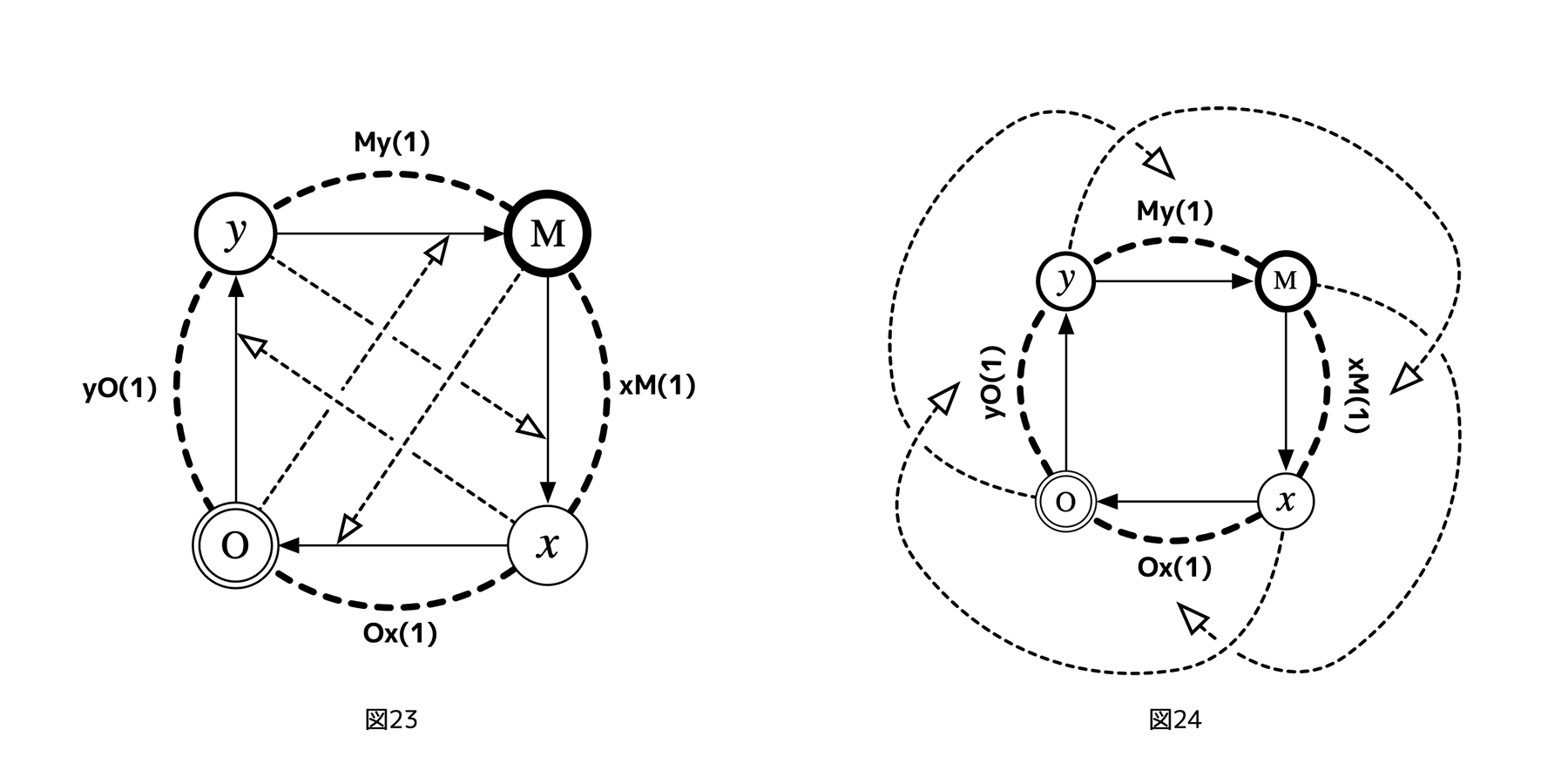［図23］［図24］
という風にできる。つまり、フェアネス評価が互いにターゲットを共有しないことで、（フェアネス評価自身によって追加された）利害関係が双方向評価にならず、かつ、フェアネス評価のターゲットとなる利害関係を、方針通り、全て同時に1以上のランクにできる（ただし、先に述べた対角4レイヤーサイクルの場合、ターゲットとなるレイヤーの利害ランクは2なので、この点では対角4レイヤーサイクルの方が優れている）。なお、我々が元々考案した図式は、3レイヤーサイクルや、後に述べる5レイヤーではなく、このタイプの非対角4レイヤーサイクルであった。
（4レイヤーでの）利害関係に対するフェアネス評価の難点
フェアネス評価として「制御の評価」を入れたことで、非対角4レイヤーサイクルは、3レイヤーサイクルをふたつ結合しただけになってしまったともいえる。
したがって、3レイヤーサイクルと類似する難点が生じ、
+ フェアネス評価のターゲットとなる利害関係が、その起点もしくは終点に、フェアネス評価者自身のメタ・レイヤー、オブジェクト・レイヤーのどちらも含まないようにできない
たとえば、利害関係yOへのxによるフェアネス評価の場合、yOは、xのオブジェクト・レイヤーであるOを含む。それを回避するため、もし、より遠い利害関係Myをターゲットにしたとしても、今度はxのメタ・レイヤーであるMが、利害関係Myに含まれる（図23上にある網掛け参照）。よって、非対角4レイヤーサイクルで達成可能なメタ・フェアネス強度は1である。ただし、3レイヤーサイクルの場合と違い、オブジェクトかメタ、どちらか一方をフェアネス評価者の直接の利害関係から除外することはできる。
また、非対角4レイヤーサイクルの場合、参照レイヤーxからみて、フェアネス評価のターゲットは、
+ メタ・レイヤーMとオブジェクト・レイヤーOへの距離が非対称になる。
という余計な属性を持ってしまう。
これは、先に見たように、4レイヤーサイクルへのフェアネス評価の入れ方が、xからyへの経路に応じ二通り存在することに対応する。たとえば、yが関係する利害関係yOへのフェアネス評価をxがする場合、利害関係Myを評価する場合に比べ、xの介入余地が大きくなる。また、そもそも利害yOへのフェアネス評価と、yへのOの制御は、とても内容が似通っていて、このことはx、O、y間に余計な結託を生む要因になりかねない。かといって、利害関係Myをxからのフェアネス評価の対象にすると、今度は、Mというx自身を制御するレイヤーを、利害関係Myへのフェアネス評価を通じ、間接的に制御できてしまう。
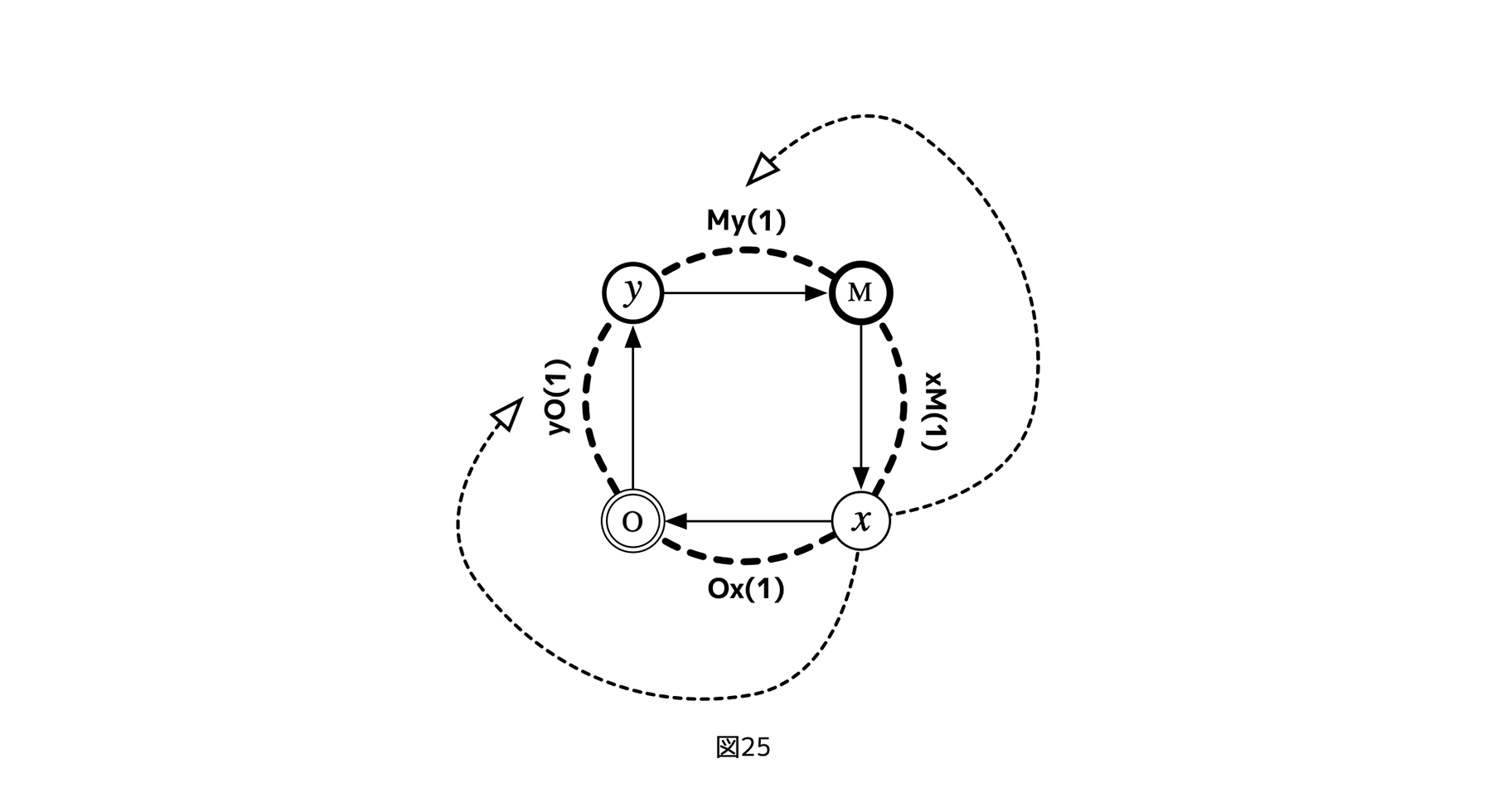［図25］
4レイヤーサイクルの利点
以上、順を追って4レイヤーサイクルが、冒頭の方針を達成する可能性を検討した。
対角4レイヤーサイクルは、
+ ランク2以上の利害ランクへのフェアネス評価を導入できる
という3レイヤーサイクルには無い利点を持つ。
さらに、後に述べる5レイヤーサイクルに比べれば、レイヤー数が少ないので、
+ レイヤーなど、図式要素の意味が解釈しやすい
という利点もある。
一方、対角4レイヤーサイクルには、
+ フェアネス評価自体が追加の双方向評価を導出してしまう
という大きな難点がある。
だが、これを避けるため、非対角4レイヤーサイクルとすると、
+ メタ・フェアネス強度が3レイヤーサイクルと同じ1にまで落ちる
…という難点を避けられない。
よって、4レイヤーまでの図式では、方針を達成することができそうにない。
5レイヤーの場合
4レイヤーサイクルの難点を避け、すべての利点を兼ね備えた図式を作りたいとすると、以下で述べるように、5レイヤーが、冒頭の方針で与えた条件を全て満たすことのできる最小のレイヤー数だということになる。4レイヤーサイクルと同様、5レイヤーサイクルでも、フェアネス評価のターゲットをレイヤーにするか、利害関係にするかで2種類の場合分けができる。
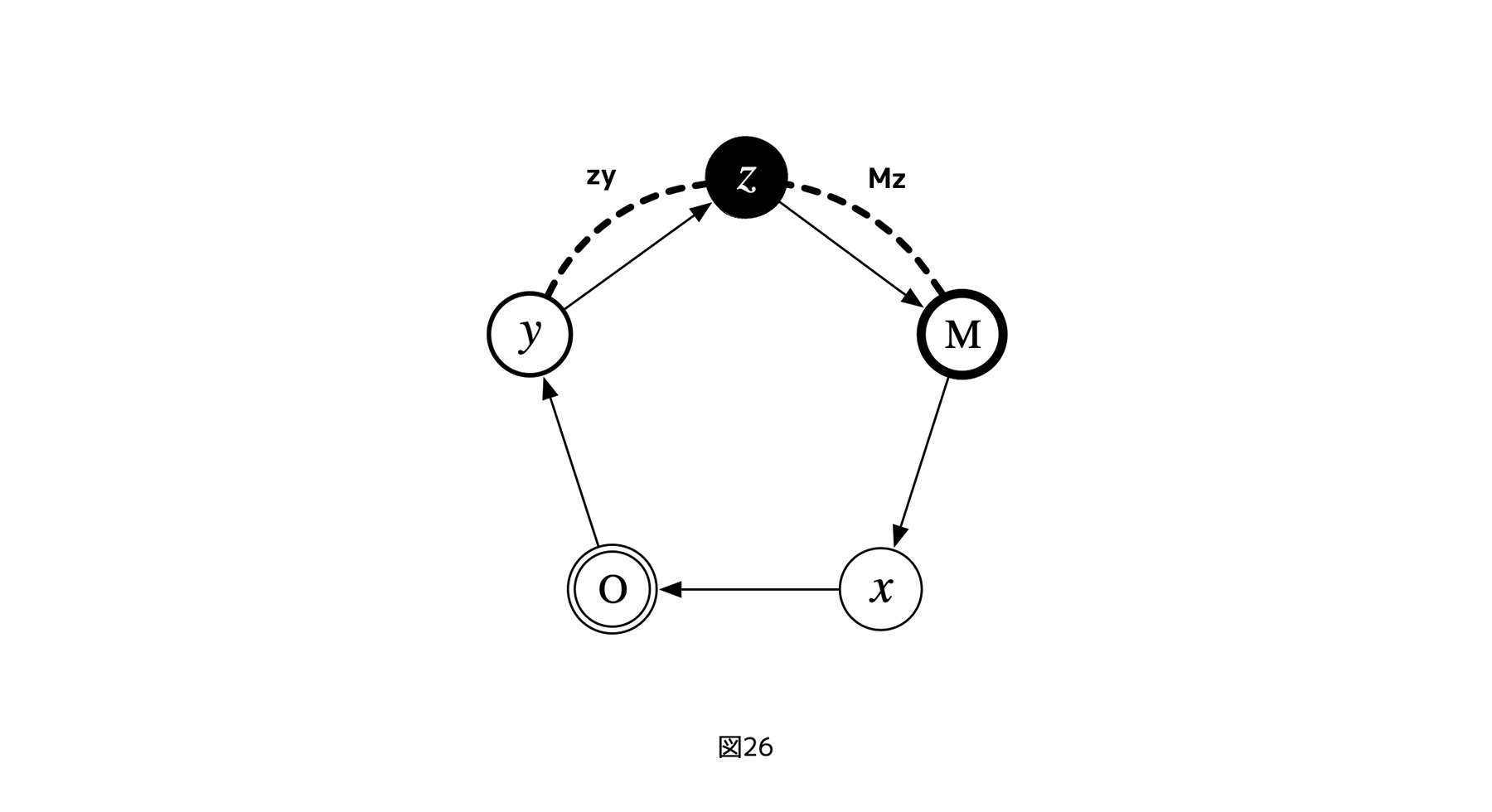［図26］
非対称5レイヤーサイクル
フェアネス評価のターゲットをレイヤーにした場合、下図のような評価構造になるだろう。図27では、xを参照レイヤーとした利害ランク、図28では各フェアネス評価矢印の起点からみた終点のランクの数値が記入されている（図29は図28の別表現）。
この図式を、「非対称5レイヤーサイクル」と呼んでおく。たとえば図28にあるように、あるフェアネス評価矢印を軸とした左右反転に対し、図が対称にならない（xzM, xzyOの形状が違う）から「非対称」と呼んでいる。次に述べる「対称5レイヤーサイクル」との対比でこのネーミングになっている。なお、4レイヤーサイクルと同じネーミングルールなら、「対角5レイヤーサイクル」としてもいいが、対角線がフェアネス評価になることが問題になるわけではないのでその名前は採用していない。
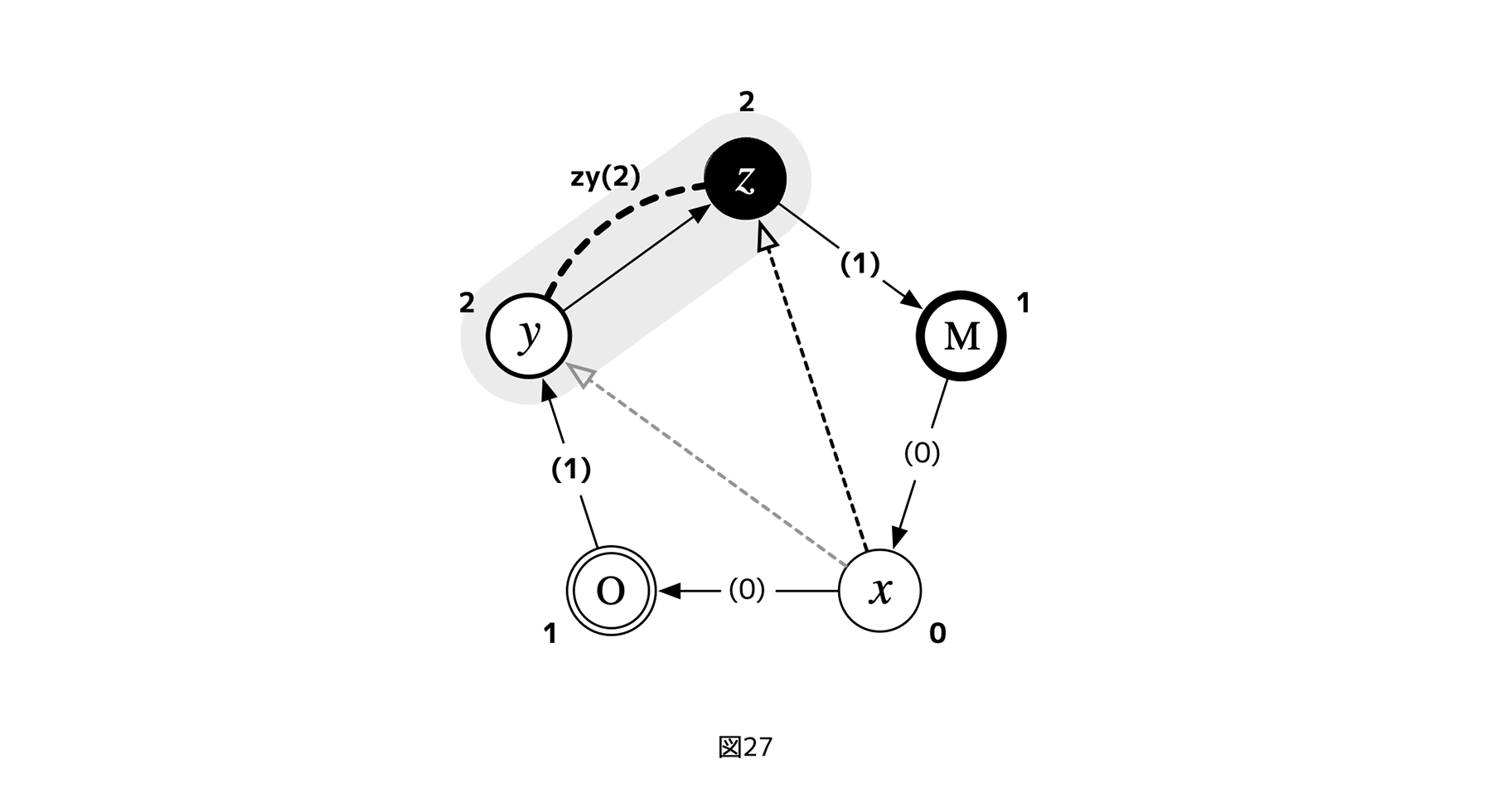［図27］
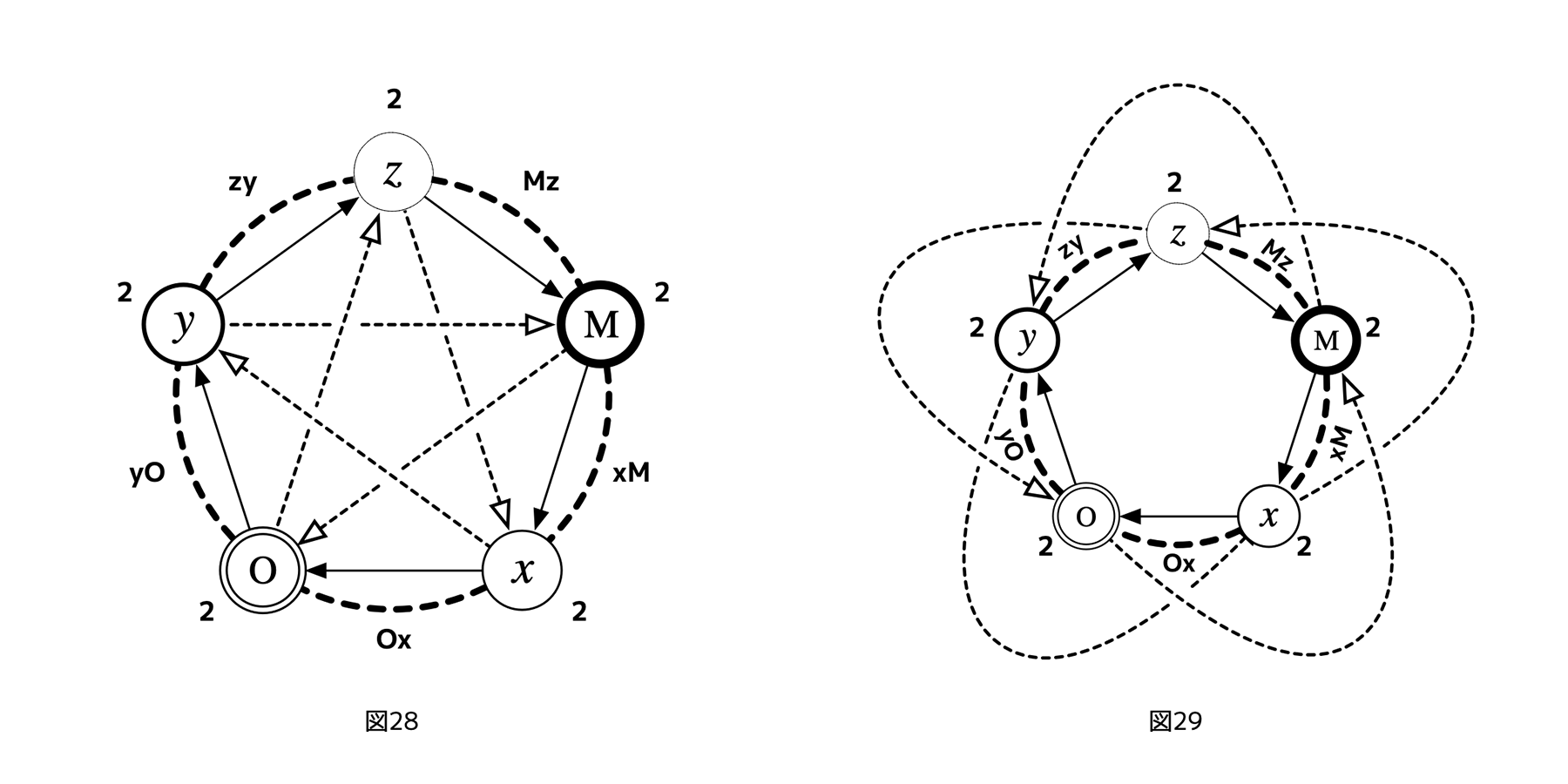［図28］［図29］
非対称5レイヤーサイクルの利点
非対称5レイヤーサイクルの利点は、4レイヤーサイクルのときに予告したように、ここで初めて、図式全体のメタ・フェアネス強度が2になる。つまり、フェアネス評価矢印の追加によって新たに双方向利害関係を導入することなく（指針3）、すべてのフェアネス評価の起点から測った終点の利害ランク（＝フェアネス強度）を同時に（指針2）、2以上（指針1’）にできる。したがって、指針の1’、2、3が、ここで全て実現できたことになる。
よって、指針を満たすという意味では、非対称5レイヤーサイクルで十分だが、まだ付加的な問題が生じる。
非対称5レイヤーサイクルの難点
非対称5レイヤーサイクルの場合、フェアネス評価者からみたフェアネス評価ターゲットのランク数が、数え上げ時にレイヤーを辿る経路に依存する。たとえばレイヤーxを参照とするzのランク数は、Mを経由した場合は2となるが、Oとyを経由した場合は3となる。これが次の難点を生むことになる。
その難点は、たとえば、xOという制御に対し、Oからのフェアネス評価OMとxへの制御Mxを合成したOMxという、xOに対する「事実上の双方向制御」を、Oが自身のフェアネス評価OMを利用して簡単に得ることができることだ（図30）。つまり、Oは、本来中立であるべきOMというフェアネス評価を用いて、xに対して影響力を行使できる。
これは、おそらく実用上も欠点となる。また、これを避けるため、フェアネス評価矢印のだけを全て逆転させたとしても、OMxという経路は無くなるが、今度は、Ozxが生じてxOが双方向制御になってしまう（図31）（他にも、たとえばxOに対し、OyMx、OyZx、OyzMxなどの双方向化も可能ではあるが、レイヤー数が多くなると同意を得るのが難しいので、3レイヤーに比べて実現可能性が低くなる）。
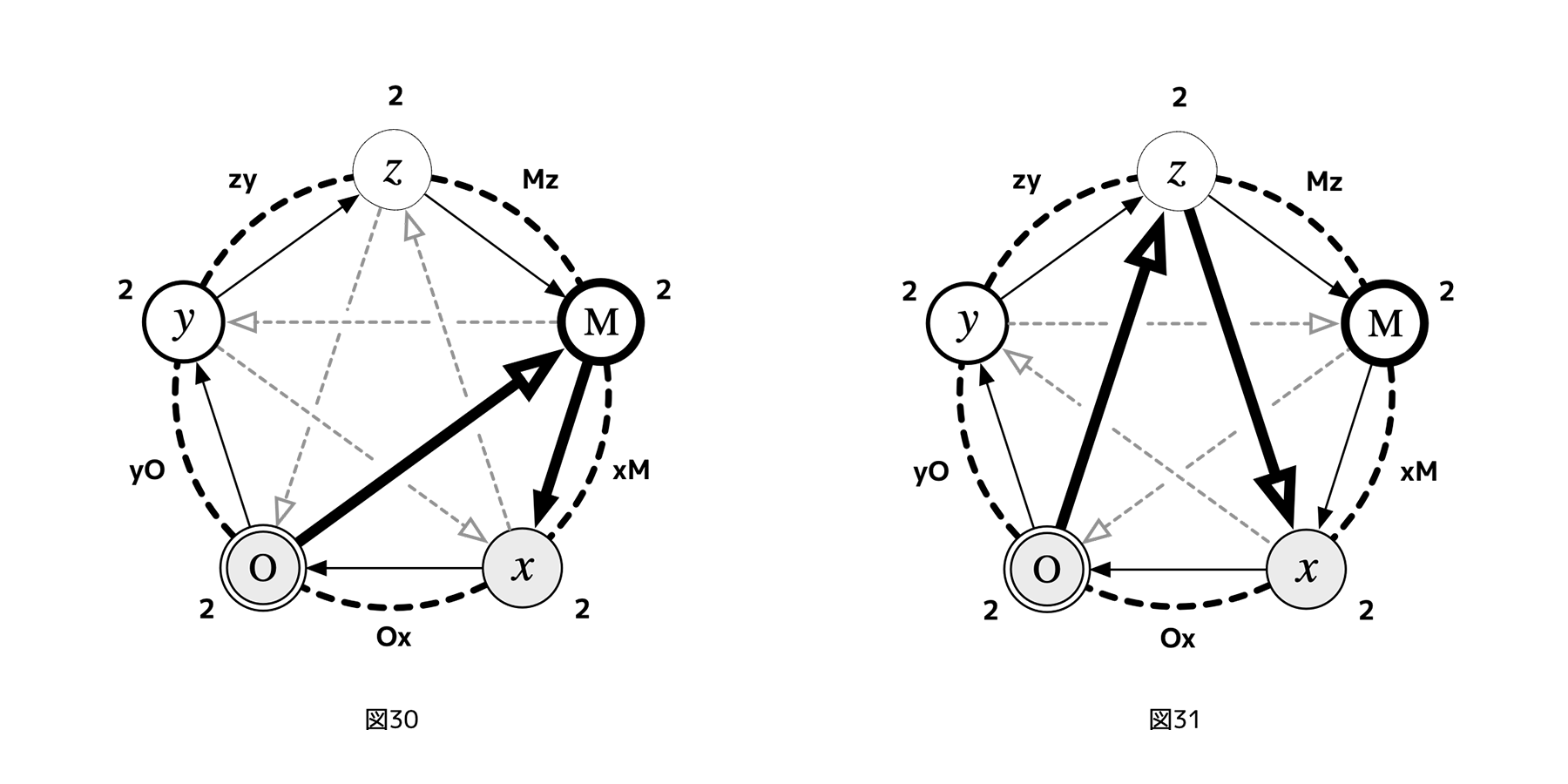［図30］［図31］
これは対角4レイヤーサイクルとは異なるタイプの双方向制御の出現である。つまり、3レイヤー、4レイヤー、5レイヤー、それぞれの図式で双方向化が違う形で出てきて、抑制する仕方も異なる。難点となる制御の双方向化は、3レイヤーの場合、フェアネス評価者の利害レイヤーが、フェアネス評価のターゲットとなる利害関係に含まれること、4レイヤーの場合、対角線上のフェアネス評価が双方向になること、5レイヤーの場合、フェアネス評価を利用した双方向制御の合成が可能になること、である。そして、3レイヤーの場合はレイヤーの追加、4レイヤーの場合は非対角フェアネス評価の利用によって抑制を図っていた。
5レイヤーの場合どうなるだろうか？非対称5レイヤーサイクルの双方向化を抑制するためには、対称5レイヤーサイクルが必要になる。
対称5レイヤーサイクル
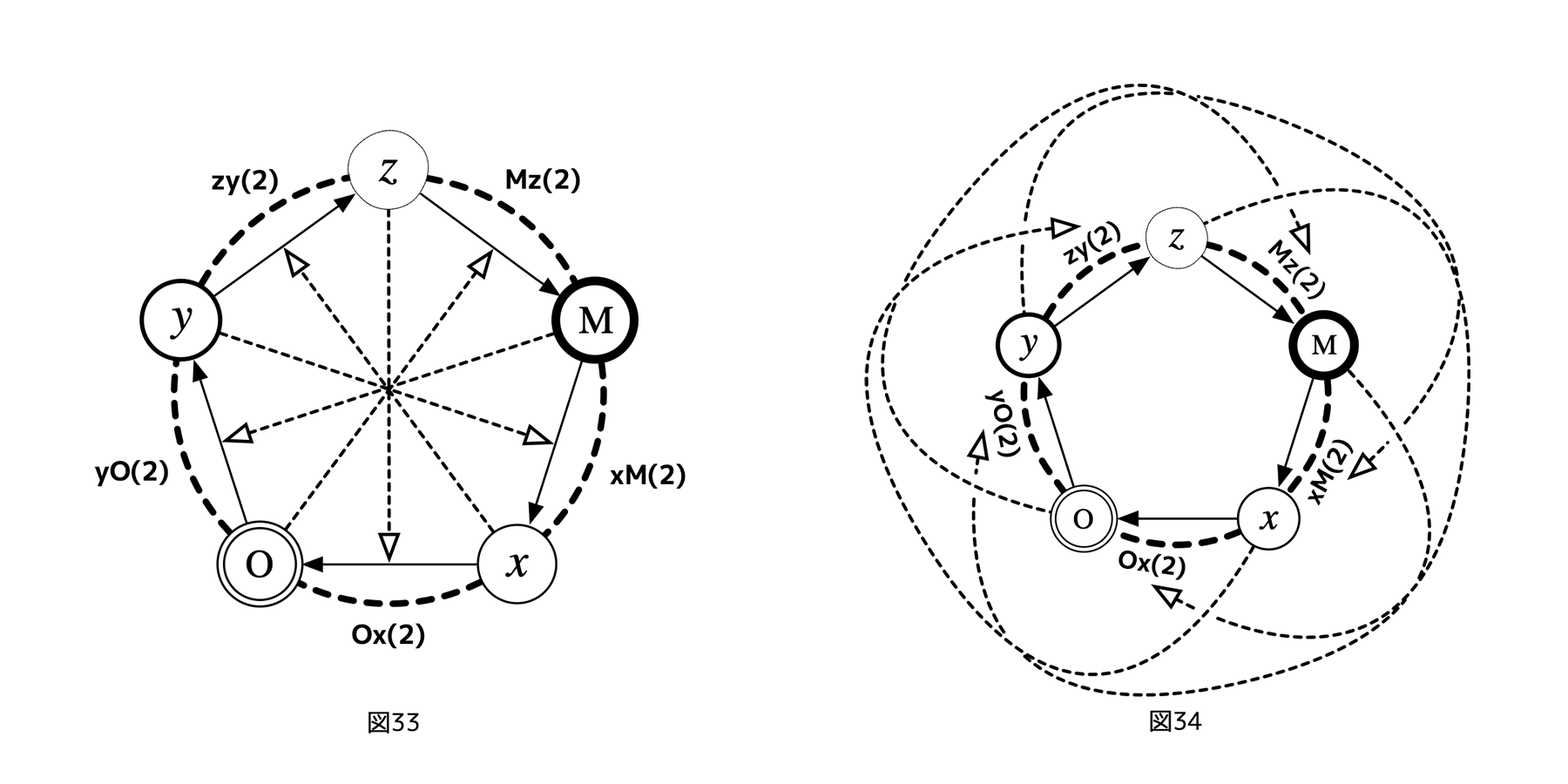
非対称5レイヤーサイクルの双方向化を抑制するために、以下に示す対称5レイヤーサイクルを導入する。対称5レイヤーサイクルでは、フェアネス評価のターゲットを利害レイヤーではなく利害関係へと移行させる。例えばxを参照レイヤーとすると、そのターゲットは、図32にあるように、zyという利害関係になり、この関係のxからみた利害ランクは2である。参照レイヤーをxにしたまま、同時に全てのフェアネス評価を記入すると、図33、図34のようになる。
［図32］
［図33］［図34］
対称5レイヤーサイクルの利点まとめ
ここまでで達成した条件を列挙する。
1. 任意のレイヤーxにとって「（xからみた）利害関係ランク」が、なるべく高い（＝遠い）制御、もしくは、「（xからみた）利害レイヤーランク」がなるべく高いレイヤー、を「レイヤーxからみたフェアネス評価のターゲット」にする
2. 1の、「フェアネス評価ターゲットランク」が、参照レイヤー（たとえばx）の取り方に依存しない
3. 構造変化、あるいは実運用によって、新たな制御や評価の双方向化が導出されない
これらの条件が満たされていることは、対象5レイヤーサイクルの図形的な性質からも明らかである。
指針1－3に加えて、経路依存性を利用したフェアネス評価の悪用（双方向制御）も消すことができた。結託するレイヤーが3以下の双方向化も抑制できた。
つまり、こうすることで、フェアネス評価するターゲットの利害ランクを同時に2以上にでき、しかも、非対称5レイヤーサイクルと違い、フェアネス評価と制御の合成による経路依存、即ち、フェアネス評価者のターゲットに対する非対称性、が生まれないようにできたわけだ。
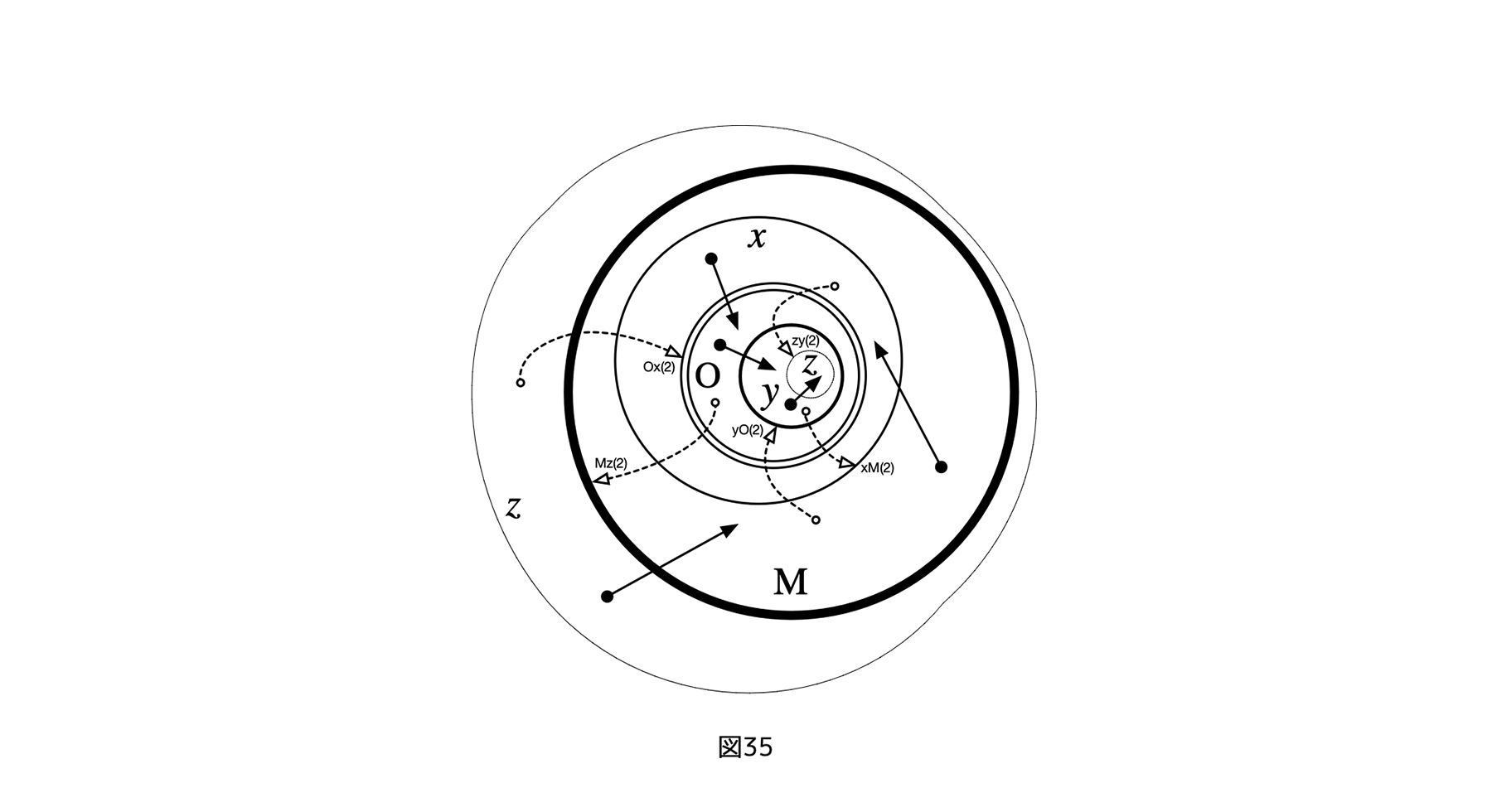［図35］対称5レイヤーサイクルのフレーム表現
補足：対称5レイヤーサイクルの具体例に対する検討
以上の考察は、具体例を全く伴わない抽象的な図式の特性についての議論だった。実際、レイヤーサイクルは、最初たんに「図式」と呼ばれていた。なので、レイヤーサイクルが具体例を持ちうるのかどうかは自明ではない。
では、対称5レイヤーサイクルに当てはめることが適当であるような、具体的なレイヤーは何かありうるだろうか？
レイヤーを大きな社会に対して具体化した場合：足りない、あるいは不明なメカニズム
現在特に目立つレイヤーで、前稿「権力分立と希望の幾何学※6」で提案した、世界、国民、政府とは別に独立性の強いもの二つを挙げると、たとえば、戦争（軍隊・警察は含まない）、金融（中央銀行など）が考えられる。法的には、戦争は政府、あるいは世界の一部、逆に現実的には金融は政府の一部、となる場合もある。つまり、政府、金融、戦争の関係は曖昧であり、歴史を見れば常に融合と分離を繰り返してきている。
仮に、戦争と金融を、世界、国民、政府に加えるとして、サイクルのどこに挿入すべきだろうか。中央銀行などの金融当局は、世界の状況に左右されて動き、国民の生活を下支える（あるいは崩壊させる）から、世界→金融→国民、という形で金融を入れることができる。一方、戦争はたとえば外国の侵入のような世界の動きに対して行使され、世界（外国）を制御するから、政府→戦争→世界となるだろう。
先に「戦争（軍隊・警察を含まない）」と書いたのは、軍隊が直接国民に向けられる事態を除外するためだ。その状況では、軍隊は警察力として、政府によって行使（行政）されていると解釈しないと、国民と戦争が直接つながってしまう。たとえば、クーデターや暴動の鎮圧などでも、建前上、なんらかの法的根拠を伴って行う（非常事態宣言、など）ことになっているから、戦争→政府→国民、と解釈はできるだろう。
つまり、5レイヤーサイクルの具体例として、世界→金融→国民→政府→戦争（→世界）を考えることができる。
各レイヤー間の権力関係は、具体的には以下のような事象として現れる。
- 世界→金融 世界情勢の変化や、国家間の取り決めの結果として、金融は自らの施策を変更することになる。
- 金融→国民 金融緩和、あるいは引き締めは、国民の生活に直接影響を与えることになる。
- 国民→政府 国民は、選挙、デモ、世論形成などの方法で政治に参画する。
- 政府→戦争 政府は軍事力の発動を決定する、また、戦争を回避する外交的努力をする。
- 戦争→世界 他国への侵攻、第三国からの武力介入、要人の暗殺といった形で、戦争は自国以外の国(=世界)の支配を目指す。
では、フェアネス評価は、具体的にどのような形で行われると想定出来るだろうか。フェアネス評価の対象は形式的には以下のようになる。
- 政府→「世界→金融」
- 戦争→「金融→国民」
- 世界→「国民→政府」
- 金融→「政府→戦争」
- 国民→「戦争→世界」
これを具体的に考えるとどうなるだろう？
政府が「世界→金融」をフェアネス評価する。これは、世界が金融を支配すべきなのに、逆に金融が世界をコントロールしているとき、政府が金融規制を行う、と言い換えることができる。
戦争が「金融→国民」をフェアネス評価する。これは、金融が国民をコントロール（景気制御など）すべきなのに、逆に金融が国民にコントロール（財政ファイナンスなど、短期的に国民に都合の良い制御を行う）されているとき、戦争が国民に規制を行うと言い換えられる。この場合、具体例を思い浮かべるのは困難だ。強引にひねり出すならば、戦争時の国債発行の必要性が、平時の野放図な国債発行、金融緩和に抑制的に働く、ということが考えられる。これはつまり、戦争があり得るという可能性が、人々を抑制的に振る舞わせるということだろう。
世界が「国民→政府」をフェアネス評価する。これは国民が政府をコントロールすべきなのに、逆に政府が国民を制圧してしまっているとき、世界が政府に対して圧力をかける。現実的に分かりやすい例で、ある国のクーデター後に起きた圧政が国際世論の非難対象になるなどが考えられる。
金融が「政府→戦争」をフェアネス評価する。これは、政府が戦争をコントロールすべきなのに、逆に戦争が政府をコントロールしている状況に対して、金融がフェアネス評価を行うという形式である。この場合、金融は、国債発行を抑制することで、戦争に突き進む政府の動きを抑えることが期待される、などが考えられる。
国民が「戦争→世界」をフェアネス評価する。これは、戦争（の損失が無限になりうる恐怖）が世界（外交関係）をコントロールすべきなのに、逆に戦争が世界（外交関係、得失が計算可能なゲームとして考えたときの利害関係）にコントロールされているとき（第一次世界大戦など）、国民が、世界市民的なコントロールで戦争状態の暴走を抑制する、という形として考えられる。だが、これを可能にする仕組みはまだ考え出されていない。
戦争が「金融→国民」を評価する場合と、国民が「戦争→世界」を評価する場合の2つは、解釈が多少、牽強付会だと言わざるを得ないだろう。恐らくここには、現在の世界にまだ存在していない仕組みが入るはずだ。たとえば、当初は形式的整合性のためだけに生み出された虚数という概念が、後に物理の計算になくてはならないものになるというように、形式的な思考の産物は、未だ発明されてない何かの位置を指し示している可能性がある。むしろ、そこを考えられるようにするところに形式的な議論の意味があると考えたい。
身近な対象に対して具体化した場合：フェアネス評価による「メッセージ」
実は4、5レイヤーサイクルは、具体例無しに、先に冒頭に書いた原則が守られるにはどうすればいいか、という形で抽象的に考えられた。4つ以上のレイヤーを持つ権力分立では、同じ役割を持つレイヤーであったとしても、そのレイヤーの挿入箇所によって、サイクル内の前後や位置によるフェアネス評価対象の違いなど、で意味が変わる。そのため、そのことを考慮に入れた洗練が本来求められる。
しかし、ここでは、この恣意性を度外視して、一つ例を考えてみる。具体例を通じて、今までは考慮に入れていなかった、フェアネス評価を通じて暗黙の意図を伝えようとする「メッセージ」というものを定義するためだ。なお、その目的のため、レイヤーを「人」に擬人化している。
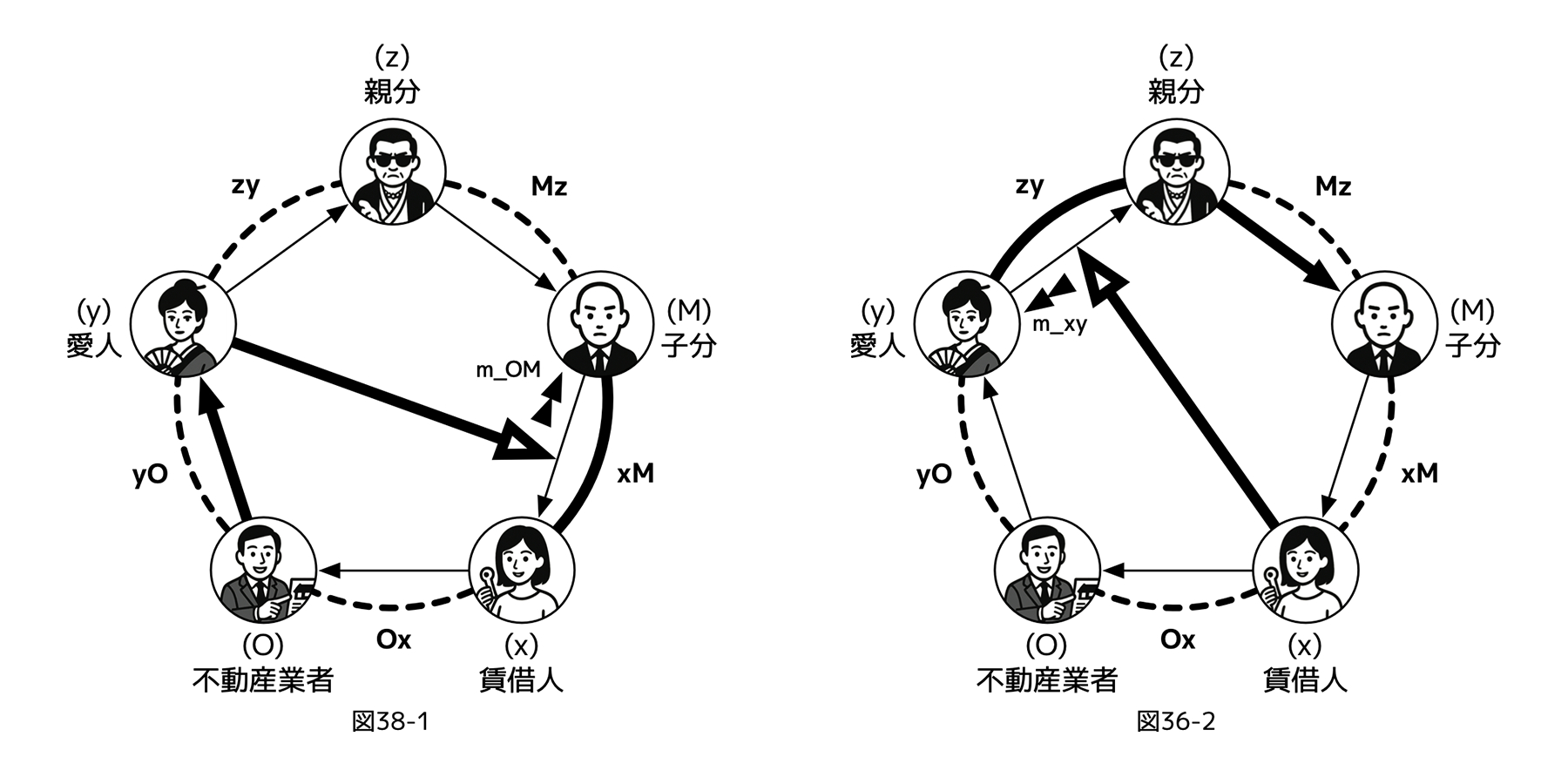
図36の非対称5レイヤーサイクルで、たとえばレイヤーxからの制御xOに対し、長さを度外視して、可能な双方向化経路O…xを例を作ってみる。O(Mz)Mx、Oy(xM)x、Oyz(Ox)x、 OyzMx（ただし、括弧内は経路に含まれる中継点がレイヤーではなく、制御チャネルであることを表す）などがあるだろう。たとえばO(Mz)Mxは、Oが自身の行うフェアネス評価を介してMzを制御し、それはMを介して、Mxを変えうるから、結局、Oxという癒着的制御の迂回路版になっている。つまり、ここで上げた例は、制御xOを双方向化するために可能な「仮想」制御（＝事実上virtualの、 Oxという方向を持つ元々存在しない制御の合成）の例となっている。
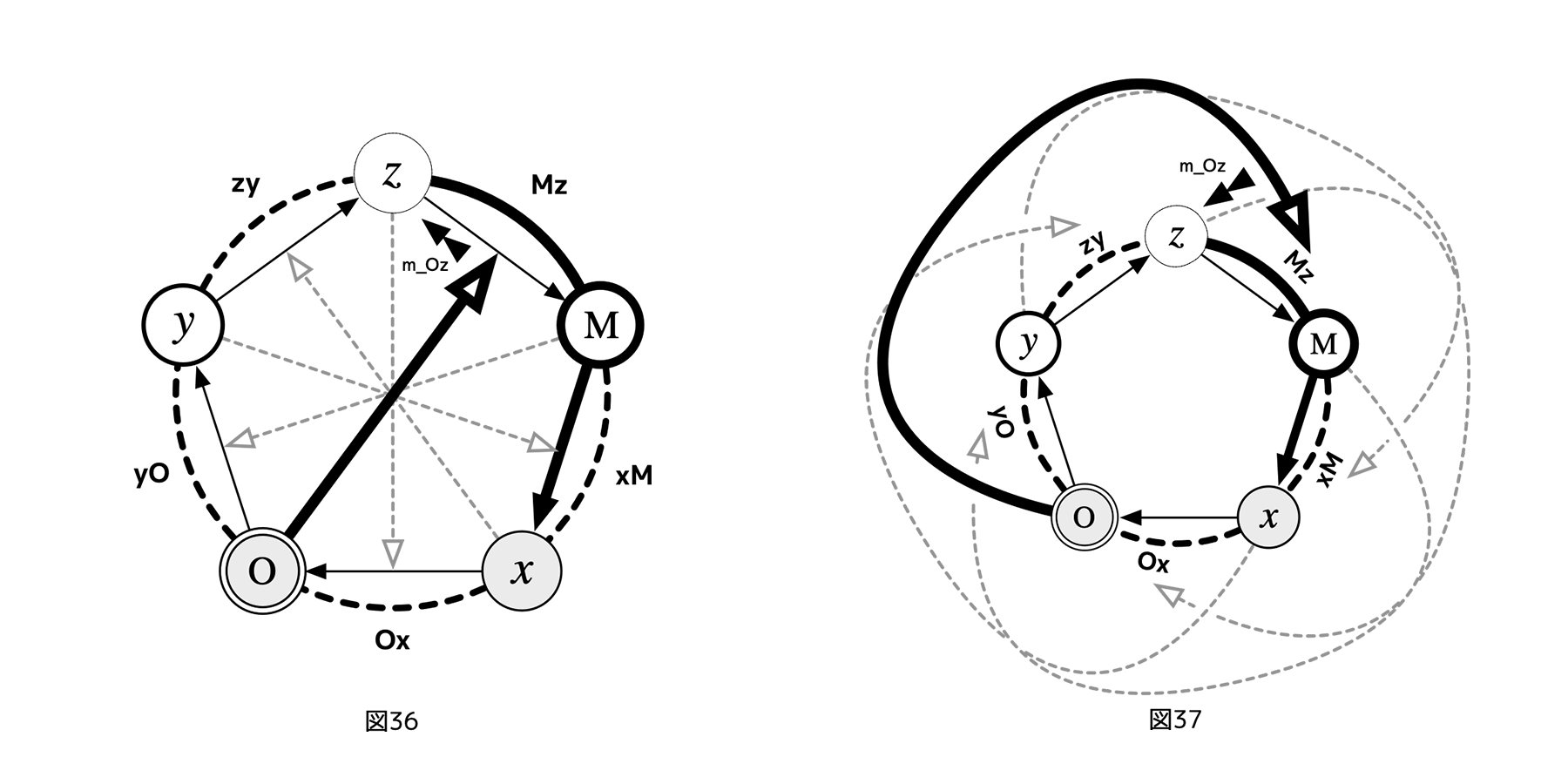
ここで、最も短い経路で、Oがxからの制御xOに対抗する操作を試みる。すると、
（1）Oから、（本来あるべき方向とは逆の）癒着した制御Mzに向かうフェアネス評価への影響（Mzの存在をあえて見逃すなど）を通じて、「経路O(Mz)Mxを使う＝図36、図37」
（2）yへの制御Oyを通り更に、yから癒着した制御xMに向かうフェアネス評価への影響を通じて、「経路Oy(xM)xを使う＝図38、図39」
という2つの方法がありうる。
（1）経路O(Mz)Mxを使う「メッセージ」
［図36］［図37］
（1）の場合（上図）、制御MzへのOからのフェアネス評価O(Mz)を歪めることで、制御Mxを（Oが望むように）変更することができる必要がある。たとえば、Oが、xからの制御xOのあり方に不満をもつときに、Mがxへの制御を通じて脅かす、などが考えられる。しかし、OはMに直接接続していないので、フェアネス評価を用いてその目標を達成するには、Oからのフェアネス評価O(Mz)のターゲットである制御Mzに含まれるレイヤーzが、なぜかOからMzへのフェアネス評価に含まれる操作（＝意図不明ならノイズ）だけで、Oの望むように制御zMでMに働きかけ、その結果、制御Mxに影響を与える、という「間接的にzを巻き込んだ操作」が必要になる。これは、一人のレイヤーに対するフェアネス評価を操作するだけで双方向化できた非対称5レイヤーサイクルに比べ、Mzというzを含んだ利害関係を媒介とする分だけ難易度が高く（つまり、実現性が低く）なる。
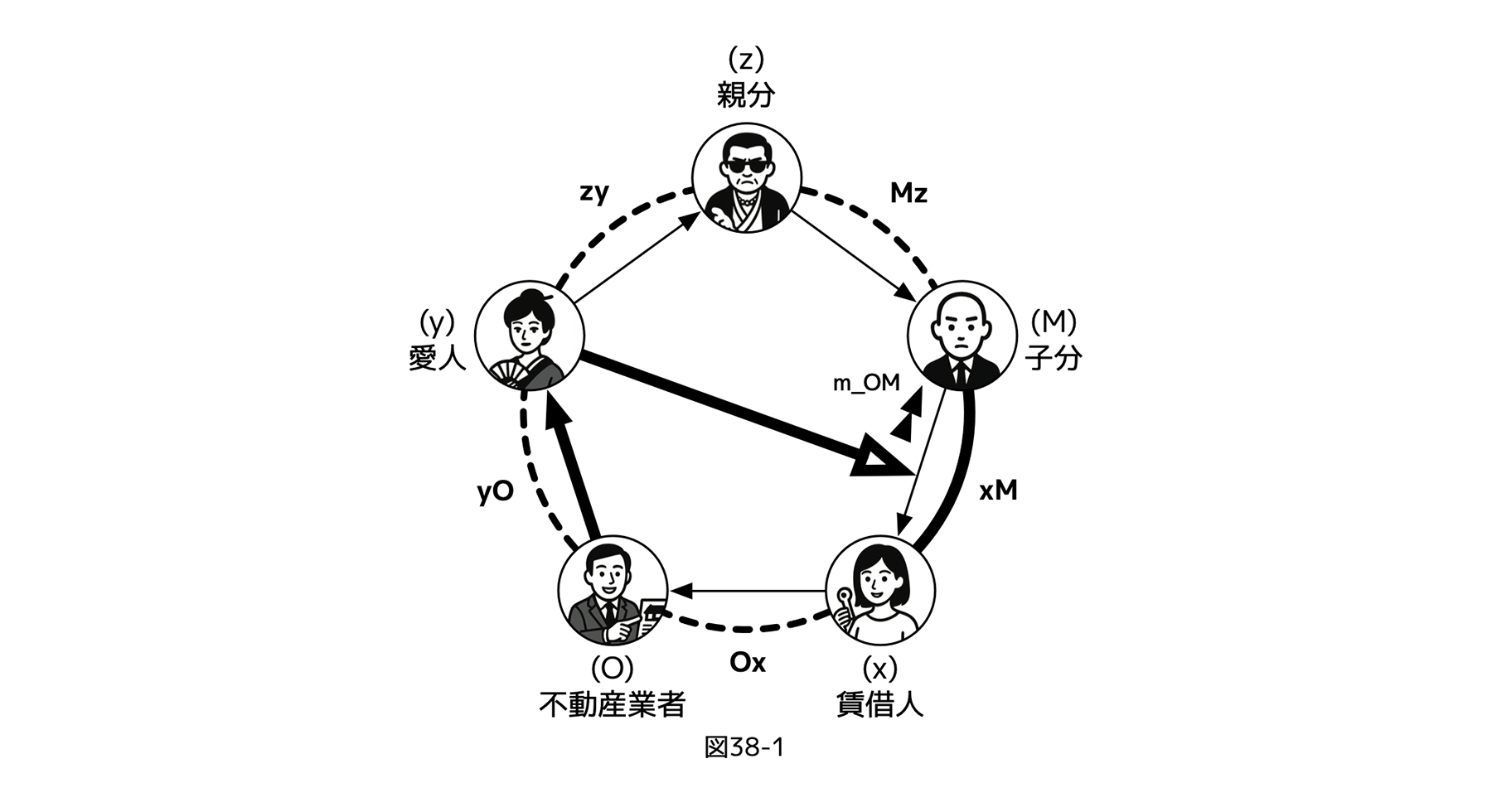
ここで、先にみたように世界→金融→国民→政府→戦争というレイヤーで具体例を考えるとあまりに複雑になってしまう。そこで想像しやすいように擬人化を採用し、（1）を、zをヤクザの親分、Mをその子分、xを家を借りるひと、Oを公正でない取引をする不動産業者、yをヤクザの愛人と具体化してみる（下図参照）。
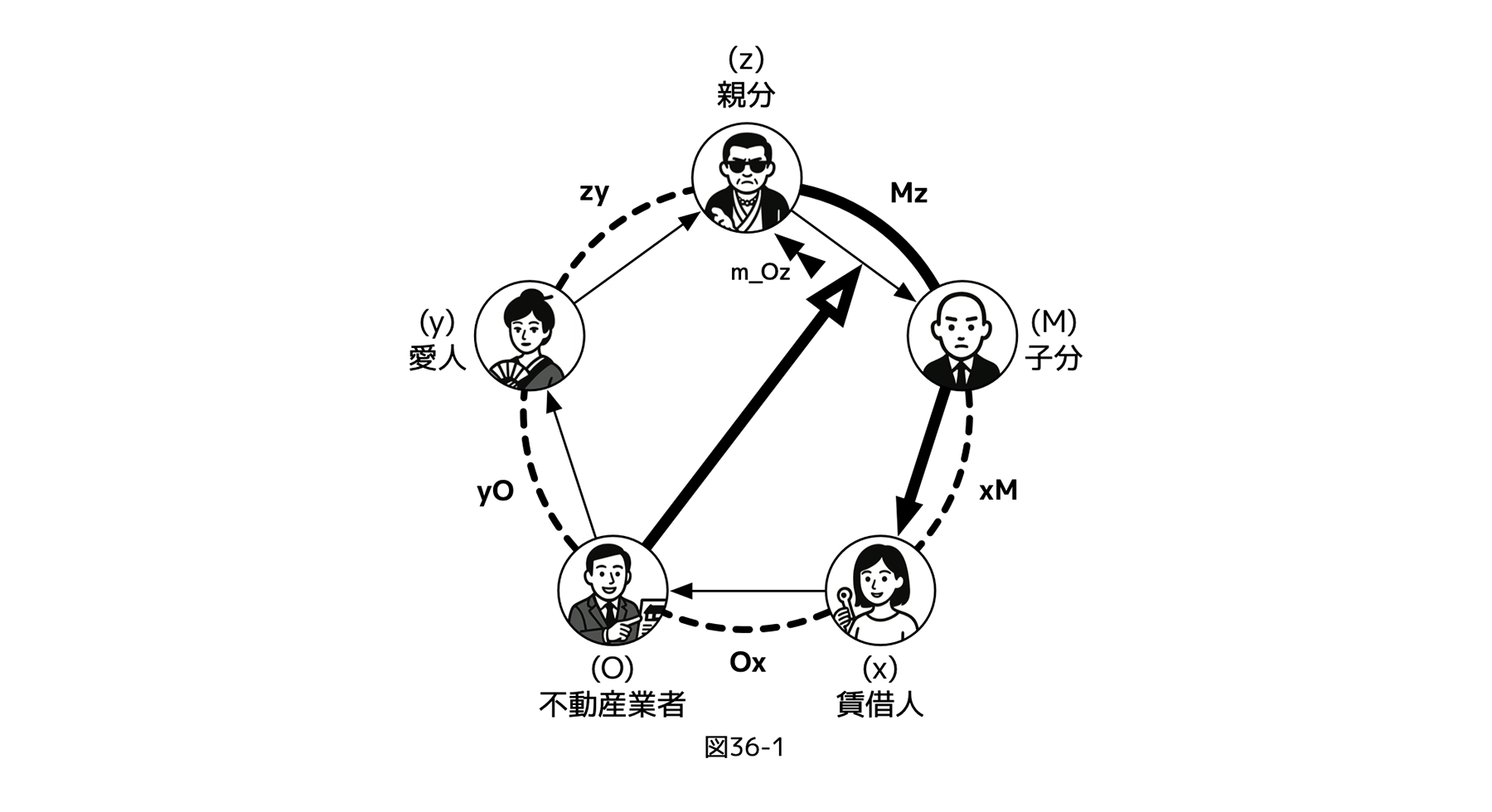［図36-1］
図36-1のような権力分立構造があるとき、不動産業者Oは、（たとえば）手数料の二重取りを貸借人xに告発（矢印x→Oの評価）されたくないため、「（制御）親分→子分」へのフェアネス評価の仕方やニュアンスを通じて親分zに働きかけ（＝zに理解可能な「メッセージ」を送る）、zの子分Mを通じ、貸借人xに告発しないように圧力（Mによるxへの暴力のほのめかし、など）をかけようと試みることができる。図36-1上でその「メッセージ」は、不動産業者Oのフェアネス評価矢印の終点から、z方向へ向いた二重三角形（メッセージ「m_Oz」）で示されている。
具体的に説明すると、不動産業者Oは、「親分zの子分Mに対する制御」へのフェアネス評価を変化させることで親分zに働きかけ、メッセージを受けた親分zが子分Mに対して、貸借人xに告発をやめるように圧力をかけるように指示する、ということになる。
これは一見すると、ここまでの議論では正しい操作ということになる。しかし、癒着的制御Mz(親分→子分)をターゲットとしたフェアネス評価O(Mz)は、「（zMではないから）親分zを直接操作できない」ところにポイントがある。もし、親分zと不動産業者Oとの間に図式外の関係が無いなら、親分zは、制御Mz(親分→子分)に対する不動産業者Oのフェアネス評価変更操作という「メッセージ」を、無意味な変更（＝ノイズ）としてしか解釈できないはずだ。
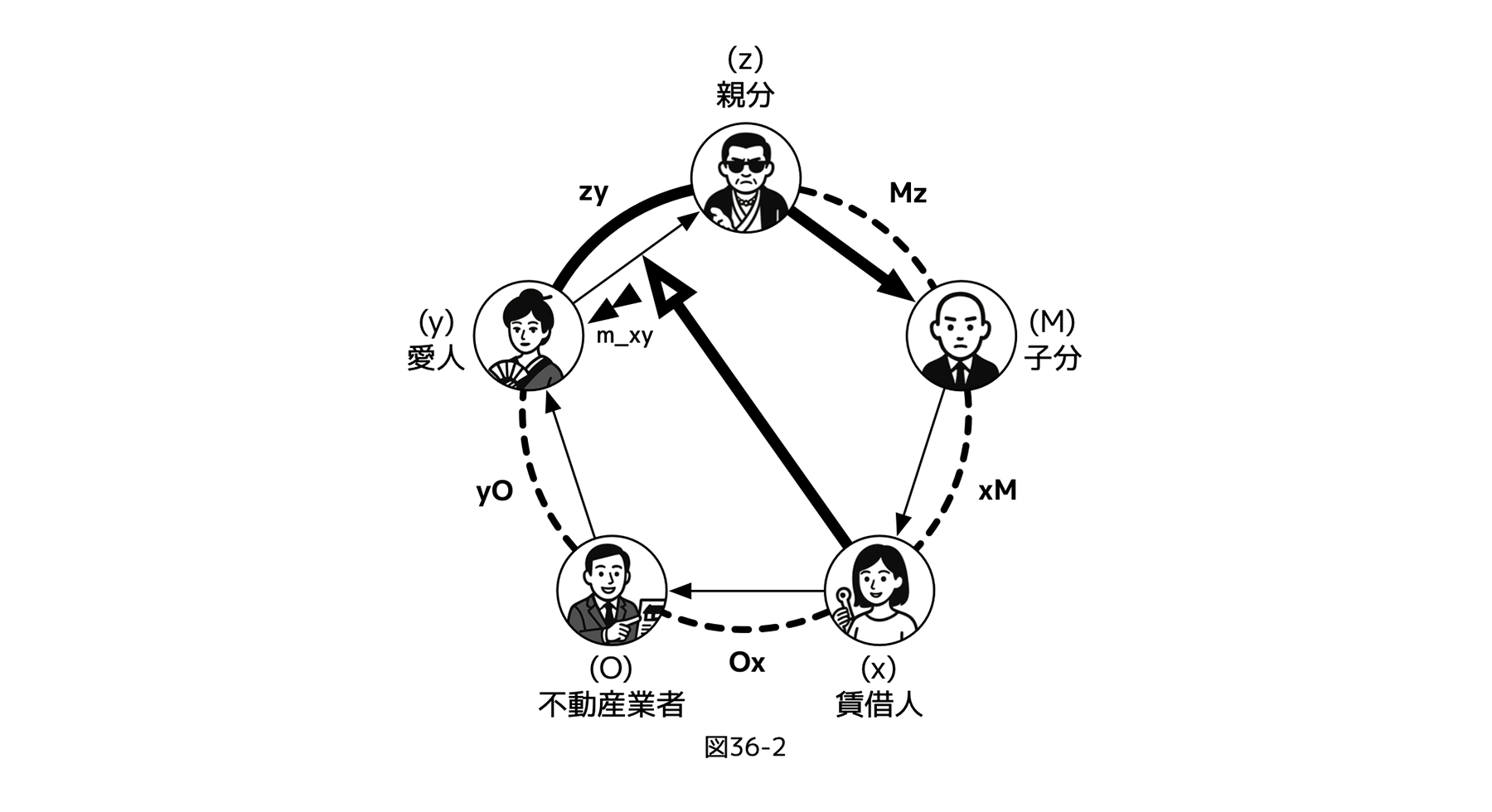［図36-2］
一方、親分zに不動産業者Oの「メッセージ」が解釈可能ならば、さらに愛人yにも賃借人xからの「（先ほどとは別の）メッセージ」が解釈可能だと（つまり、図式外のやりとりを）仮定することもできるだろう。全体で図式外メッセージを送り合うことが可能な状況（図36-2）だ。このとき、賃借人xは、制御yz(愛人→親分)のフェアネス評価者でもあるので、もし、賃借人xが制御zy(愛人→親分)へのフェアネス評価x(zy)を通じた「メッセージ」を愛人yに送り、その結果親分zへの働きかけが可能なら、zMxという経路を使った脅しに対抗できるだろう。
具体的には、貸借人xが、「愛人yの親分zに対する制御」への評価を変化させることで愛人yに働きかけ、メッセージ（例えば、浮気の事実を掴んでいる、など）を受けた愛人yが親分zに、子分Mを貸借人xにけしかけるのをやめさせる、となる。
するとこの場合、賃借人xは制御zy（親分-愛人）を通じた親分zの操作を通じ、不動産業者Oの制御Mz(子分-親分)を通じた親分zの操作と張り合うことができる。
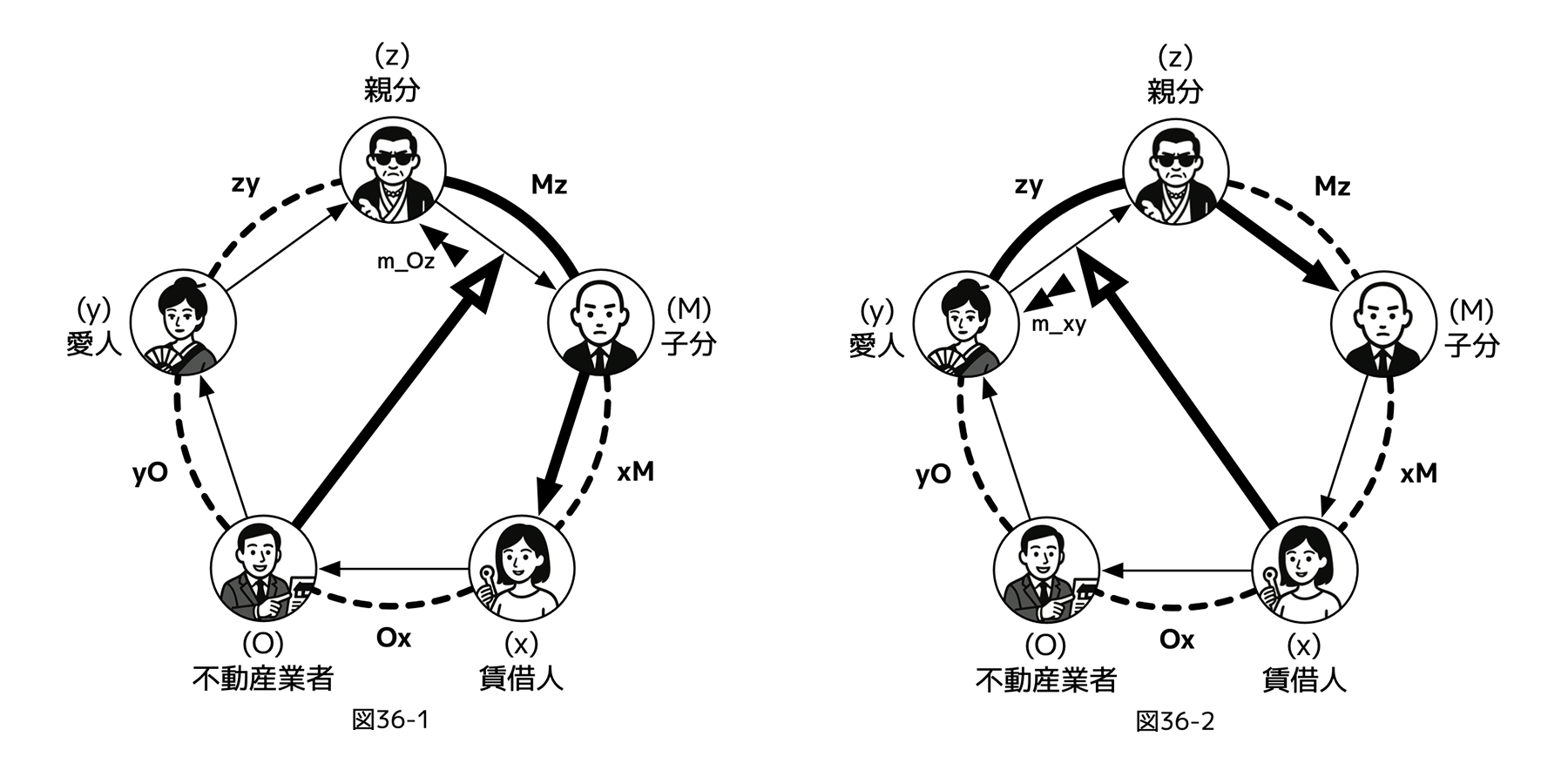［図36-1］［図36-2］
つまり、「メッセージ」の解釈（＝「不動産業者Oから制御Mz(親分→子分)へのフェアネス評価O(Mz)を通じた子分Mの操作、つまり、m_Oz : O(Mz)→M」と「貸借人xから制御zy(愛人→親分)へのフェアネス評価x(zy)を通じた親分zの操作、m_xy : x(zy)→z」）の、どちら一方しか可能でない場合のみ、xO(貸借人→不動産業者)の双方向化が可能になる。
あるいは同じことだが、両方の「メッセージ」が同時に解釈可能な場合も、解釈不能な場合も、双方向化はできない。結局その制約は、親分zという（賃借人xや不動産業者Oからみた）ランク2のレイヤーが関係することで生じ、対称5レイヤーサイクルの双方向化を（一人のレイヤーだけを操作すれば良かった非対称5レイヤーサイクルに比べ）難しくしている。
わかりやすく言えば、
+ 利害関係の当事者（xやO）の第三者（yやM）の第三者（z）を当事者が説得するのは、難しいということだ。そして、この難しさ＝フェアネス強度が全てのレイヤーにとって等しく成立するように組み合わせたのが、対称5レイヤーサイクルという権力分立構造となる
「第三者に何らかの利害調停を依頼するのはフェアである」という常識があるが、それはほとんど3レイヤーサイクルそのものだ。そして我々は、「第三者による利害調停がうまくいかなくなる論理」を経由し、「第三者の第三者」をシンメトリックに組み合わせたこの図式にたどり着いたことになる。
（2）経路Oy(xM)xを使う「メッセージ」
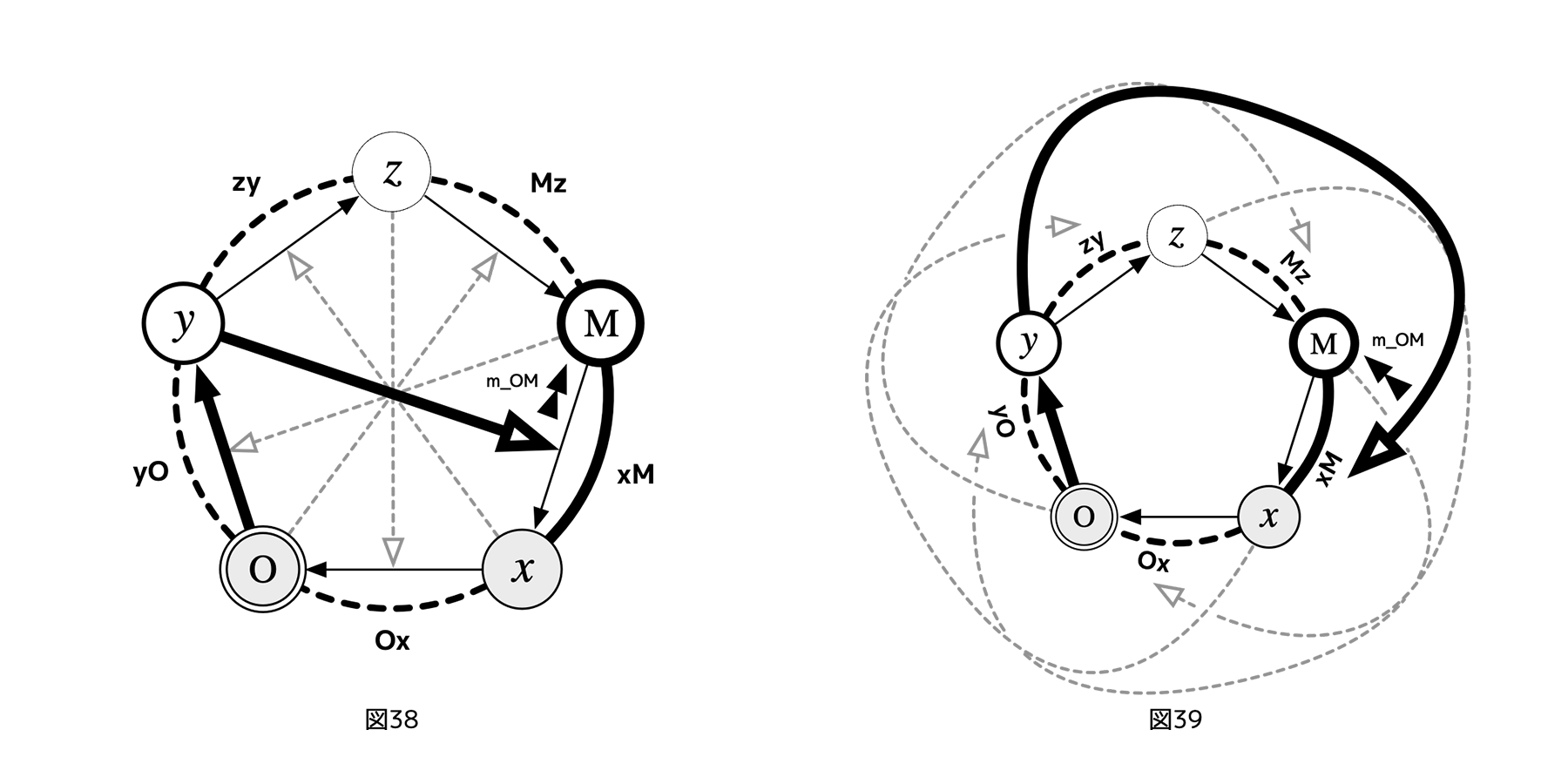［図38］［図39］
次に、（2）の場合(上図)、Oは、直接的支配関係にあり、かつ（1）では無関係であったyを通じ、制御xMへのフェアネス評価y(xM)を操作させ、xによるOへの制御xOに対抗しうる。
しかし制御yOは、Oからランク2の位置にいるMによってフェアネス評価M(yO)されている。このとき、「制御xMへ向かうyのフェアネス評価y(xM)」を、MがOからの「m_OM： y(xM)→ M（図の黒い二重三角形）」として解釈でき、かつ、「（メッセージに従い）Mが癒着yOへのフェアネス評価M(yO)の不正な変更を選択する」場合に、経路Oy(xM)xによる操作が可能になる。
（1）と同様、モデルケースを考えてみよう。zがヤクザの親分、Mがヤクザの子分、xが貸借人、Oが不動産業者、yはヤクザの愛人とする。不動産業者Oは手数料の二重取りという不正をxによって告発（制御）されるのを防ぐため、今回はヤクザの愛人yを懐柔することになる。愛人yは制御xM(子分→貸借人)へのフェアネス評価y(xM)を介し、ヤクザの子分Mに（不動産業者Oの意図を託した）「メッセージm_OM」を送り、子分Mが恫喝などの手段で貸借人xの告発を取り下げさせるということを試みることになる。
［図38-1］
不動産業者Oは、愛人yに圧力をかけ、愛人yは「子分Mの貸借人xへの制御」への評価を変化させることで、例えば、それまで良好だった評価をいきなり下げられた場合、そこに何かしら隠された意図を感じ、「親分zへの裏切り行為の秘密を知っているのではないか」などの勘ぐりが生じる（＝「メッセージm_OM」）。ここで図式以外の伝達手段（メッセージの意味を解釈する方法）があれば、この揺さぶりを通じて、子分Mに貸借人xに告発を取り下げるように圧力をかけさせることができるだろう。
しかし、「メッセージ」の理解可能性を（1）の場合と同様、すべてのフェアネス評価について同等と仮定するなら、この場合でも、貸借人xは、制御zy(愛人→親分)へのフェアネス評価x(zy)（たとえば貸借人xは「愛人yの浮気暴露」などができると仮定する）を通じ、親分zへ「メッセージ（m_xy : x(zy)→z）」を送り、親分zの子分Mに対する支配（制御）を、貸借人xに有利に変更してもらう（浮気暴露により、親分zは愛人yに興味がなくなったので、子分Mが愛人yの言うことを聞かないよう言う、など）ことで、身を守ることができる。よってこの場合も、「メッセージ」の解釈可能性がどちらか一方のペアでのみ偏って可能なときに限り、双方向化が起きる。
［図38-1］［図36-2］
ここで「メッセージ」と呼ぶものは、図式の外に伝達手段がない場合はノイズでしかないと書いたが、それが脅迫メッセージとして解読できるなら、ノイズとは言い切れない。上述したケースでは、フェアネス評価の「メッセージ」を全てのレイヤーが解釈できるか、もしくはすべてのレイヤーが解釈できなければ、問題は生じなかった。しかし、片方だけが「メッセージ」として機能し、もう一方は機能しないので、対抗できない、というような状況は現実には生じ得る。
元々、図式外の関係が存在していなければ「メッセージ」が解釈できないので、問題は生じない。しかし、図式外の関係は、恐らく、あらゆる権力分立が形骸化する潜在的、かつ本質的な理由であり、しかも、それが生じるのはほぼ不可避だ。ここでの結論は、対称5レイヤーサイクルでは、図式外「メッセージ」が存在しても、偏在していなければ（＝等しくどこにでもあれば）図式の効力に影響しない、と解釈できる。以上のような検討は、図式外「メッセージ」が存在するケースを少しずつ対処可能なものにしていく一里塚になるだろう。
なお、そもそも現実の権力構造に照らし合わせれば、上のような事例では、（レイヤーサイクルのような権力分立ではなく）ヤクザの親分が単独で権力を握るトップダウン構造となっているのが自然だ。だから、この例はあくまで、5レイヤーサイクルの運用をシミュレーションして理解しやすくすることを目的にしている。
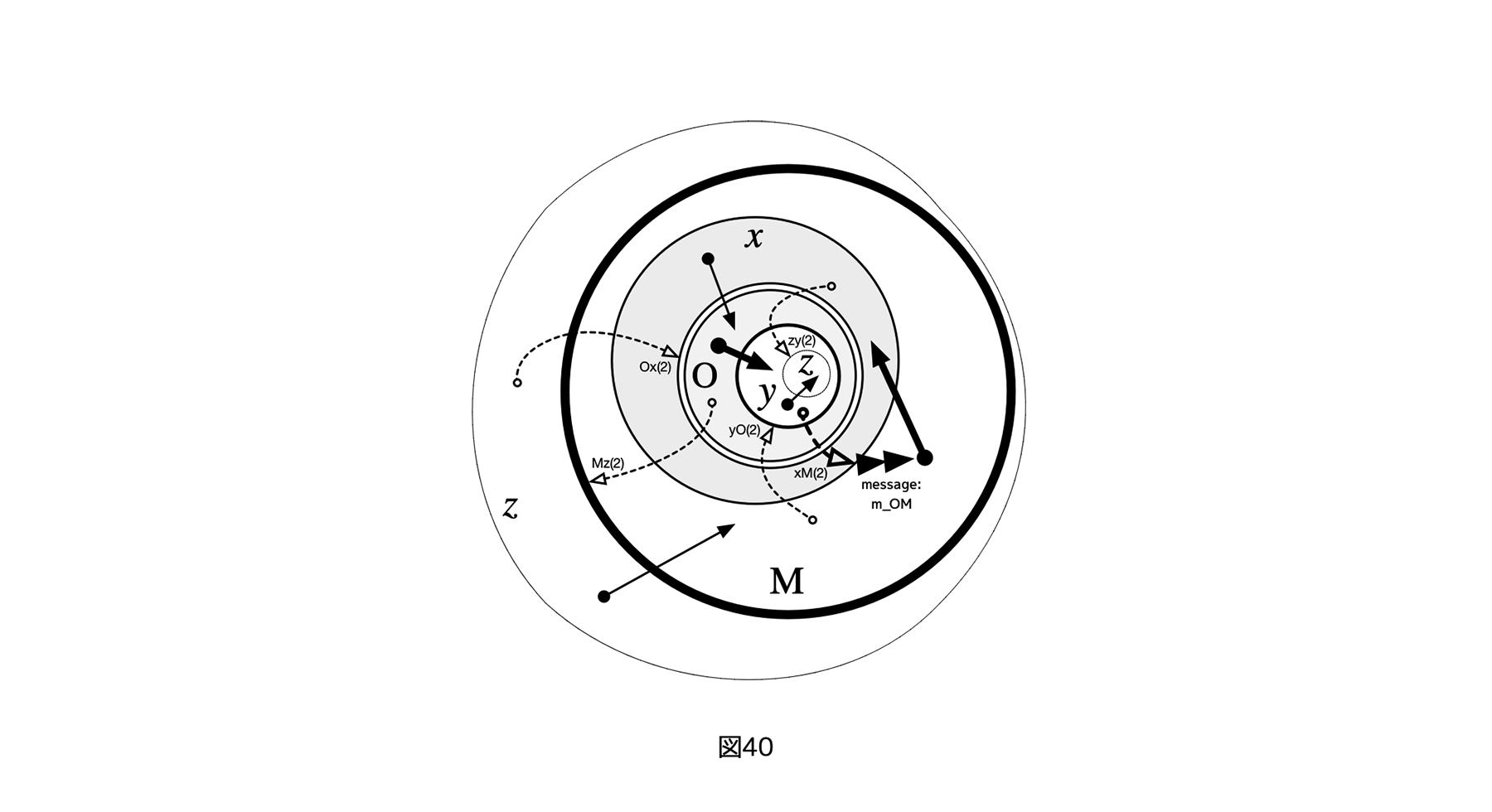［図40］メッセージ付き対称5レイヤーサイクルのフレーム表現
結び
我々はまず、好ましい権力分立のありかたとして、(1)絶対的な権力者を認めない、(2)第三者機関の中立性をあてにしない、(3)権力を監視する者を監視する者を監視する者…といったメタレベルの無限後退に陥らない、という三つの条件を考え、それを満たす権力分立として3レイヤーサイクルという形式を提示した（権力分立と希望の幾何学）。
さらに、レイヤーサイクルにおける制御の双方向化や逆転という「劣化」を防ぐために、サイクル内にある直接の制御（利害）関係のないレイヤーによるフェアネス評価が必要だと考えた（「壺の断面が歪むとき※7」）。
このとき、3レイヤーサイクルではフェアネス評価のターゲットと主体の間に充分な距離をとることができないという問題が生じた。そこで、レイヤー数を一つずつ増やして順に検討したところ、フェアネス評価をする主体とターゲットの利害ランク（距離の遠さ）を2以上にでき、しかも、フェアネス評価と制御の合成による双方向制御を行うのが困難である構造として、対称5レイヤーサイクルにたどり着いた。
つまり結論として、好ましい権力分立を行うためにレイヤー数は最小で5必要だということになった（本稿）。
ただし、この議論は形式的なものであり、5つのレイヤーに具体的に何を当てはめることが適当であるかは分からない。ここでは仮に、世界、金融、国民、戦争、政府（そして、ヤクザの親分、子分、家を借りる人、不動産業者、親分の愛人）というレイヤーを当てはめ、その制御とフェアネス評価による介入のあり方の例を考えてみた。とはいえ、この具体例には牽強付会なところや空白が存在し、不十分なものであることは認めざるを得ない。
ここでの議論は、現状では具体性に乏しく、机上の空論と言うべきものだろう。しかしこれは夢想ではなく、形式的な議論である。だからこそ、先に「権力分立と希望の幾何学」でも触れた通り、市場が必要でなくなるほどの計算力をもつAIが意思決定を担うような極端な未来を想定したとしてもなお、その有効性があると期待している。
なお、本来この原稿で検討すべきだがしていないことが、具体例の恣意性以外にもいくつかある。
1）5レイヤーサイクルの具体例のところで軽く触れたように、レイヤーの挿入箇所の恣意性を除く方法はまだわかっていない。可能な入れ方全てを考慮して挿入箇所の恣意性の影響が出なくなるような方法も考えられるが、検討していない。
2）より一般の図式が存在する可能性は大きい。単純に、6以上のレイヤーまたは大きなＮの可能性があり、図形的特性、対称性が崩れた場合、単純な巡回ではなく、他の構造、トポロジーの可能性もある。
3）フェアネス評価の実装方法、チャネル自体を対象にするのが難しい場合、対象となる制御矢印の始点と終点に対する評価で置き換えることが考えられる。それがどの程度可能なのかは分からない。さらにフェアネス評価が持つべき性質や内容の特徴なども、未検討である。
4）結託を扱うゲーム理論やメカニズムデザインとの関係や、特に「フェアネス評価」が、ゲーム参加者によって行われる、ゲームのルールを順守しているかどうかのチェックであるという点が、どの程度本質的なものなのかはよくわからない。これに付随して、全体を進化ゲーム理論的な力学系としてみた場合の安定性、それぞれのレイヤーがメカニズムデザインを変え続ける場合の安定性、なども重要になるだろう。
5）哲学、精神分析の主体の構造との関係。レイヤーサイクルのような構造を着想したとき、ラカンやドゥルーズ＋ガタリといった思想家が述べていた主体の構造に関する図式が多少念頭にあった。マルチレイヤーサイクルを今の人間とは別の主体が持つ精神構造、たとえば5極構造を持つ主体のようなものとして解釈することは、きっとできるだろう。それは「超人」という曖昧な概念よりはもう少し、特定可能な、それゆえにレトリックに流されない、別の存在のあり方の形式になるかもしれず、それを「希望の幾何学」といってもいいのかもしれない。
［図41］
［図42］
［図43］
［図41］［図42］［図43］計算機設計によるロケットエンジン※8（各種制約条件をクリアし、実際に機能するが、人間は直接幾何を描いていない）
Credit:
原案：西川アサキ
草稿執筆：西川アサキ、古谷利裕
草稿修正：VECTION
同時編集：VECTION
作図：掬矢吉水
