可逆性
ものごとが可逆(reversible)であるとは、それが「逆に戻りうること。もとの状態に戻りうること※1」である。しかし、二項演算としての加減乗除の計算は、一般に可逆ではない。例えば、
\(4 + 3 = 7\)
であるが、足して\(7\)になる2つの数の組み合わせは、整数だけに限っても
\(7 = 7 + 0\)
\(7 = 6 + 1\)
\(7 = 5 + 2\)
\(7 = 4 + 3\)
\(\vdots\)
\(7 = -1 + 8\)
\(\vdots\)
のように無数にある。だから二項演算は不可逆、つまり計算の答えから元の数を一意に導くことができない。
可逆計算
可逆計算(Reversible Computation)とは、過去に遡ることができる計算のことである※2。例えば、ここで「\(\pm\)」という演算を定義してみる。この演算は、2つの数の入力に対して、その和(\(+\))と差(\(-\))の2つの答えを出力する。
\(4 \pm 3 = 7, 1\)
つまり演算 \(\pm\) は、
\(x \pm y = a, b\)( \(a = x + y\) , \(b = x – y\)
と定義できる。すると、入力 \(x, y\) は、出力(計算の答え)\(a, b から、以下の式で一意に逆算することができる。
\(x = \frac{a+b}{2}\)
\(y = \frac{a-b}{2}\)
だから、先の
\(4 \pm 3 = 7, 1\)
は出力から入力を逆に辿ることができる。
\(7, 1 = 4 \pm 3\)
これは、「\(\pm\)」の逆演算「\(\pm^{-1}\)」を用いて、
\(7 \pm^{-1} 1 = 4, 3\)
と書くこともできる。
この例のように、計算が可逆であるためには、入力と出力の数が同じであることが必要である。そして入出力の数が同じであれば、演算をつなげていくことができる。
\(4 \pm \pm \pm \pm 3 = 16, 12\)
\(\begin{pmatrix} 4 \\ 3 \end{pmatrix}\)\(\begin{pmatrix} 7 \\ 1 \end{pmatrix}\)\(\begin{pmatrix} 8 \\ 6 \end{pmatrix}\)\(\begin{pmatrix} 14 \\ 2 \end{pmatrix}\)\(\begin{pmatrix} 16 \\ 12 \end{pmatrix}\) \(\cdots\)
\(16 \pm^{-1} \pm^{-1} \pm^{-1} \pm^{-1} 12 = 4, 3\)
\(\begin{pmatrix} 16 \\ 12 \end{pmatrix}\)\(\begin{pmatrix} 14 \\ 2 \end{pmatrix}\)\(\begin{pmatrix} 8 \\ 6 \end{pmatrix}\)\(\begin{pmatrix} 7 \\ 1 \end{pmatrix}\)\(\begin{pmatrix} 4 \\ 3 \end{pmatrix}\) \(\cdots\)
\(4 \pm \pm \pm^{-1} \pm \pm \pm^{-1} \pm \pm \pm^{-1} \pm^{-1} \pm^{-1} 3 = 7, 1\)
\(\begin{pmatrix} 4 \\ 3 \end{pmatrix}\)\(\begin{pmatrix} 7 \\ 1 \end{pmatrix}\)\(\begin{pmatrix} 8 \\ 6 \end{pmatrix}\)\(\begin{pmatrix} 7 \\ 1 \end{pmatrix}\)\(\begin{pmatrix} 8 \\ 6 \end{pmatrix}\)\(\begin{pmatrix} 14 \\ 2 \end{pmatrix}\)\(\begin{pmatrix} 8 \\ 6 \end{pmatrix}\)\(\begin{pmatrix} 14 \\ 2 \end{pmatrix}\)\(\begin{pmatrix} 16 \\ 12 \end{pmatrix}\)\(\begin{pmatrix} 14 \\ 2 \end{pmatrix}\)\(\begin{pmatrix} 8 \\ 6 \end{pmatrix}\)\(\begin{pmatrix} 7 \\ 1 \end{pmatrix}\)\(\cdots\)
このように、計算を自由に進めたり戻したりすることができる。
あみだくじは可逆計算
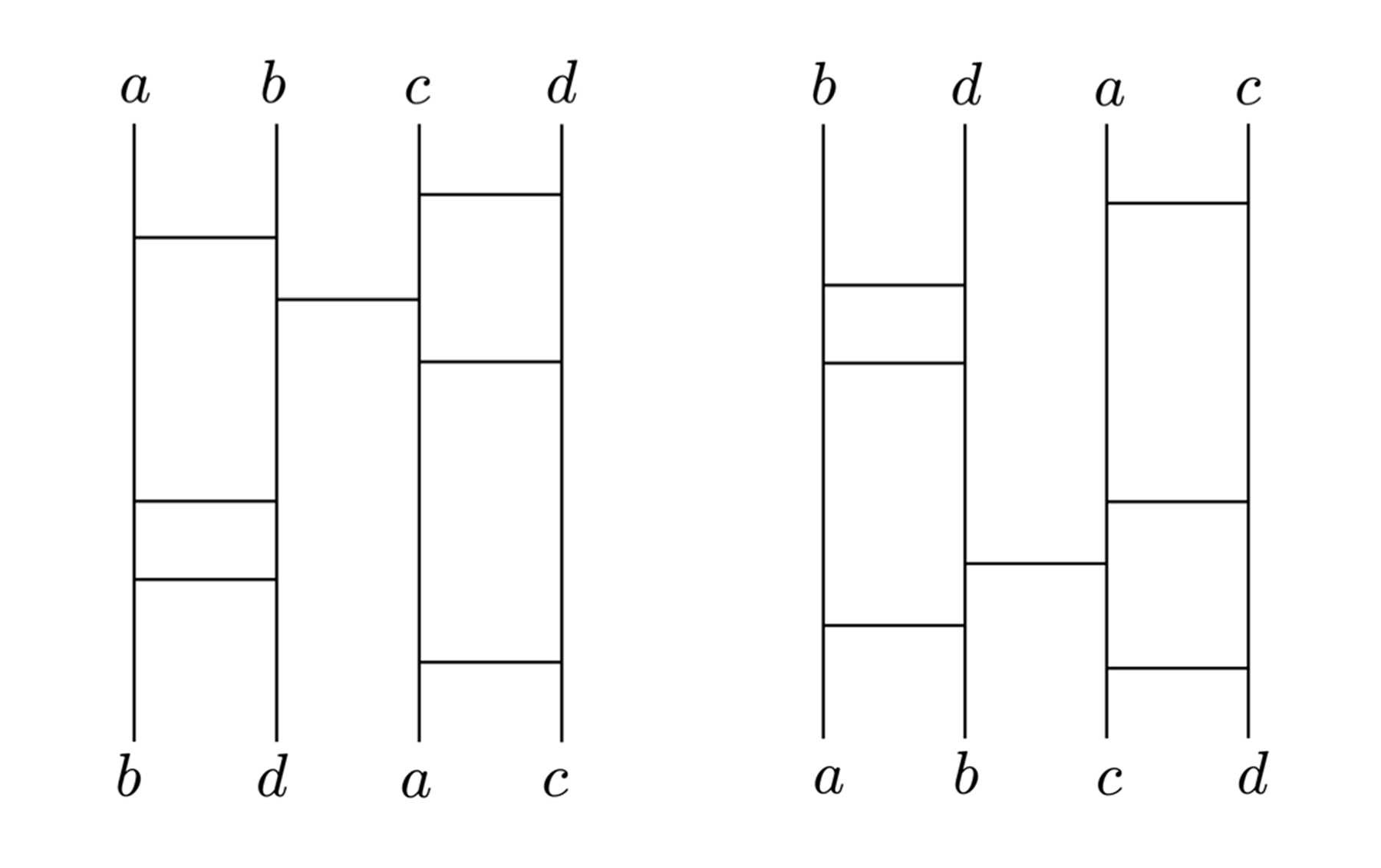
日常の中の可逆計算として「あみだくじ(Ghost leg)」をあげることができる。左側のあみだくじを上の入力(左側から\(a, b, c, d\))を、出力 \(a, b, d, c\) に変換する計算(関数 \(GL\))とすると、
\(GL(a, b, c, d) = (b, d, a, c)\)
と書くことができる。左側のあみだくじを上下さかさまにした右側のあみだくじは、その逆関数
\(GL^{-1} (b, d, a, c) = (a, b, c, d)\)
となり、以下のように可逆計算となる。
\(GL^{-1} ( GL(a, b, c, d)) = (a, b, c, d)\)
可逆オートマトン
さらにこの可逆計算の概念を、セル・オートマトンに拡げていく。セル・オートマトン(Cellular automaton)は、格子状のセルに単純な規則(アルゴリズム)を適用していくことで、セルの状態を時間発展的に変化させていく離散的計算モデルである。セル・オートマトンは非常にシンプルなシステムではあるが、そこから生まれるセルの状態や挙動が予測不能で豊かになり得ることから、計算や機械、自然や生命といった、複雑系のモデルやメタファーとしてよく用いられる。
ここでは、まず最も単純な、\(0\)(白)か\(1\)(黒)のいずれかの状態を取るセルによる、1次元のセル・オートマトンを考える。一般に、オートマトンは通常は非可逆だが、うまく規則を設定することで、可逆なオートマトンをつくることができる※3。

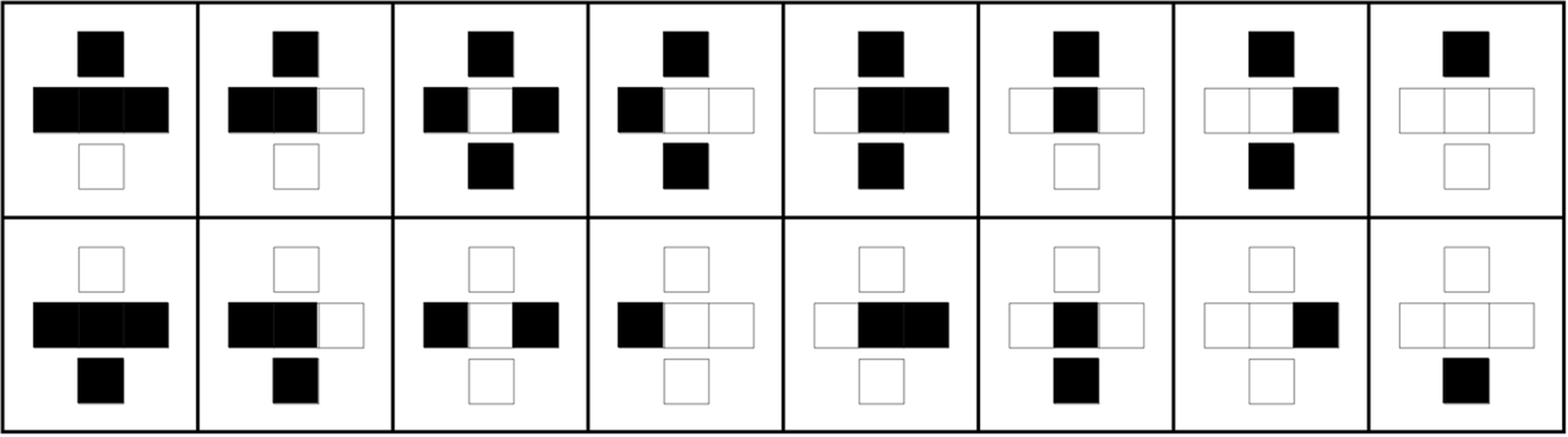
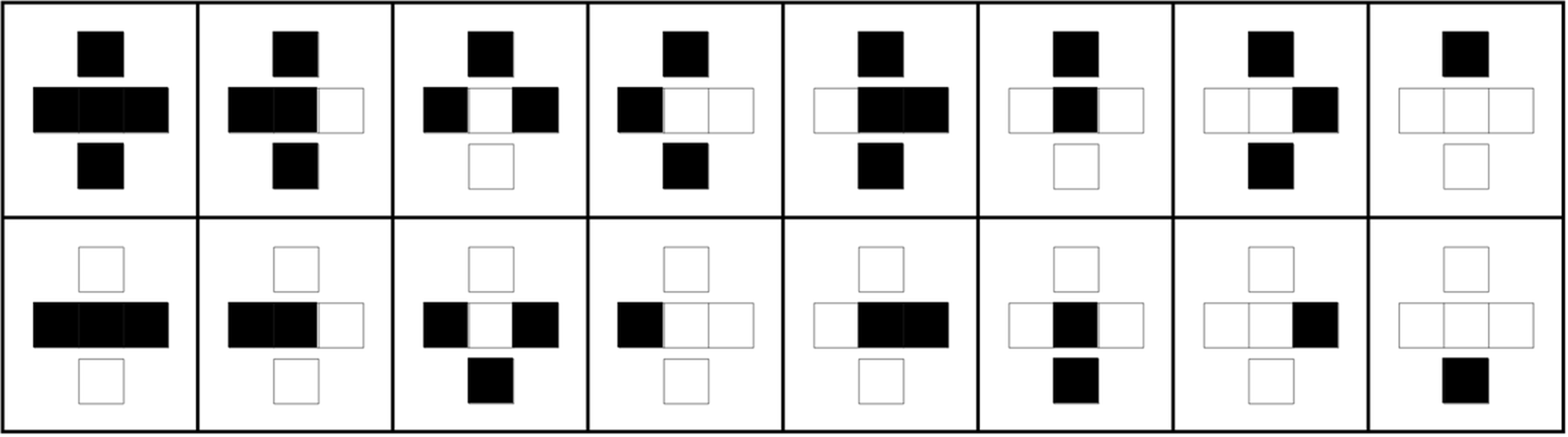
例えば、この図は可逆な1次元セル・オートマトンの一例である。右上に遷移の規則が図示されているが、これらはすべて、その要素(セルの状態)を上下逆にしても変化せず、過去と未来の役割を入れ替えることができる。このルールによって生成されるパターンは、上図のように時間の反転に対して、対称性を示している。
Mathematicaを用いた実験
実際に、この1次元可逆セル・オートマトンを、Mathematicaを用いていくつか実験してみる。
1次元セル・オートマトンのルール128(ウルフラム・コードによる表記)
RulePlot[CellularAutomaton[{128}]]
に、2ステップ前の中央セルの状態を加えて可逆化したルール128Rは、

となる。いずれのルールもそれ自体が上下対称、あるいは上下対称になるルールの組がある。これを、ランダムな状態の100個のセルから100ステップ実行すると、以下のような結果になる。
ArrayPlot[
ResourceFunction["ReversibleCellularAutomaton"][
128, {RandomInteger[1, 100], RandomInteger[1, 100]}, 100]]
シンプルで規則的な、時間的に反転可能なパターンが生成されている。しかし、可逆セル・オートマトンの中にも、もう少しいくつか、可逆オートマトンの例をみてみる。
ルール214R

ArrayPlot[
ResourceFunction["ReversibleCellularAutomaton"][
214, {RandomInteger[1, 100], RandomInteger[1, 100]}, 100]]

最初の単純な挙動の例とは異なり、このルールの場合、可逆性を有したまま、複雑な(ランダムに見えるような)パターンを生成する。そこで、同じルールでメッシュの数を500に増やして実行してみる。
ArrayPlot[
ResourceFunction["ReversibleCellularAutomaton"][
214, {RandomInteger[1, 500], RandomInteger[1, 500]}, 500]]

他にもいくつか、複雑な振る舞いをする可逆セル・オートマトンの例を見てみる。
ルール73R

同じく500個のセルを、ランダムな配置から500ステップ実行する。可逆セル・オートマトンのような特殊な系においても、通常のものと同様の複雑な挙動をとるだけでなく、「衝突」のような固有の振る舞いを見せることがわかる。
ArrayPlot[
ResourceFunction["ReversibleCellularAutomaton"][
73, {RandomInteger[1, 500], RandomInteger[1, 500]}, 500]]
ルール197R
ArrayPlot[
ResourceFunction["ReversibleCellularAutomaton"][
197, {RandomInteger[1, 500], RandomInteger[1, 500]}, 500]]
ルール37R
ArrayPlot[
ResourceFunction["ReversibleCellularAutomaton"][
37, {RandomInteger[1, 500], RandomInteger[1, 500]}, 500]]
情報は物理的である
 情報は物理的である
情報は物理的である
コンピュータは、1ステップごとのエネルギー消費が避けられない。関連した分析から、測定プロセスや通信チャネルに関する洞察が得られ、物理法則の本質に関する思索が促された。
—— ロルフ・ランダウアー
ウルフラムが、セル・オートマトンによってさまざまな自然現象や物理現象を説明しようとしている背景には、IBMリサーチの物理学者ロルフ・ランダウアー※4が1961年に提示し、議論が始まった「ランダウアーの原理※5」がある※6※7。
ランダウアーの原理のポイントは、以下の式によって、シャノンの情報量と熱を結びつけたことにある。
\(-\langle Q \rangle \geq k_B T H\)
- \(- \langle Q \rangle\):熱浴(環境)に放出する熱量 \([J]\)\(\large\)
- \(k_B = 1.380649 \times 10^{- 23} [J/K]\) (ボルツマン定数)
- \(T\):絶対温度 \([K]\)
- \(H = – ln P(E) ~[nat]\):ここで事象 \(E\) が起こる確率 \(P(E)\)とする (シャノン情報量)
この式の意味は「シャノン情報量\(H\)を《消去》すると、少なくとも\(k_B T H\)の熱が環境に放出される」ということである。つまり情報は作り出す時ではなく、例えばメモリークリアのように、それを《消去する》ときに熱を放出する。もちろん、この熱は実質的には極めて小さい。
- 1ビットのデータを消去(気温20度):
\(1.38 \times 10^{- 23} \times 293 \times ln(2) \approx 2.804 \times 10^{- 21} [J]\) → ランダウアー限界 - 1テラバイトのデータを消去(気温20度):
\(1.38 \times 10^{- 23} \times 293 \times ln(2) \times 8 \times 10^{12} \approx 2.243 \times 10^{- 8} [J] \approx 5.358 \times 10^{- 9} [Cal]\)
冒頭の可逆計算の例で示したように、可逆な過程において、入力と出力の数が一致している必要がある。しかし一般の二項演算の場合、入力の数より出力の数の方が少ないことがほとんどである。それは言い換えれば、入力の一部をゴミ(ガベージ)として、消去していることに相当する。ランダウアーの原理によれば、このとき熱が放出され、エントロピーが増大する。可逆な計算を行う際にエネルギーの消費はないが、不可逆な計算の場合、このゴミの情報量を消去するためのエネルギーが最低限必要となる。つまり、不可逆な演算の際に最低限必要とされるエネルギーは情報の消去量によって推定することができ、それが計算に必要なエネルギーをなるべく少なくしようとしたときの物理的な限界(ランダウアー限界)を規定する。
物質性や身体性とは切り離された、情報の純粋な表現として考えられていたデジタル・メディアであっても、メモリーにせよディスクにせよ、情報それ自体は必ず何らかの物理メディアで記録されなければならないことを考えれば、「情報と物質(物理メディア)、さらには情報処理と物理法則の間には、何らかの対応関係があるのではないか?」と考えるのは、ごく自然なことである。計算が論理的に可逆であるかどうかということは、その計算が計算機上で実行される際の物理的過程が、熱力学的に可逆であるかどうかということに対応しているというランダウアーの原理は、そうした疑問に対して、ひとつの指針と見方を与えてくれる。
ランダウアーの原理はその後、物理学者のチャールズ・ベネット※8や、リチャード・ファインマン※9などによって継続的に探求されていった。しかし同時に「情報のエントロピーと物理のエントロピーを同じものと考えて本当に良いのか?※10」あるいは「常識的には、情報は消去するより記録することの方が大変なこと(エントロピーが低くなっている)ではないか?※11」という疑問に根ざした異論も提示されている。とはいえ2012年には、1ビットメモリーの一般的なモデルを用いて、ランダウアーの原理が実在することが実験的に示されている※12。
可逆計算とエントロピー増大の法則
スティーブン・ウルフラムの『A New Kind of Science』の第9章「Fundamental Physics※13」では、この可逆セル・オートマトンを用いて、基本的なレベルでは可逆的な物理法則から、物質が拡散していったり、熱いものがだんだん冷えていくマクロレベルの不可逆的、すなわちランダム性が増大していくように見える日常的な現象の原理を説明している。
以下の例は、この章で示されているルール122Rの可逆的セル・オートマトンを用いて、単純なパターン(1, 0, 0, 1, 1, 1, 1, 0, 1, 1)が、箱の中で跳ね回り衝突しながら、時間を経るにつれて次第に乱雑になっていく(エントロピーが増大する)粒子のような振る舞いをすることを、実際に計算して確かめたものである。
ルール122R

ArrayPlot[
ResourceFunction["ReversibleCellularAutomaton"][122,
ConstantArray[CenterArray[{1, 0, 0, 1, 1, 1, 1, 0, 1, 1}, 97], 2],
1000]]

可逆オートマトンなので、最後の2ステップのパターンを初期値として計算を逆行すると、もとのパターンに戻っていく。
ArrayPlot[
ResourceFunction["ReversibleCellularAutomaton"][
122, {{1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0,
1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0,
1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0,
0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1,
1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0}, {1, 1, 0, 0, 1, 0, 1, 0, 0, 0,
0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1,
0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0,
1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0,
0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0}},
1000]]

しかしこの初期状態が1ビットでも異なると、元の状態には戻らず、乱雑な状態のまま計算が進んでいく。一旦エントロピーが増大すると、それを元の状態に戻すのは極めて難しい。つまり、現実的な実験では、ランダム性を減少させるような初期条件を設定することは(ほぼ)不可能であり、ミクロにみれば可逆の物理現象であっても、それは常に乱雑になる方向へと不可逆的に進んでいく(エントロピー増大の法則)。
ArrayPlot[
ResourceFunction["ReversibleCellularAutomaton"][
122, {{1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0,
1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0,
1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0,
0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1,
1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0}, {1, 1, 0, 0, 1, 0, 1, 0, 0, 0,
0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1,
0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0,
1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0,
0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1}},
1000]]

戻せるデザイン
情報が物理的であるならば、この可逆計算というモデルによって、デザインというフィジカルな活動を思索できるかもしれない。そこでまず「デザインプロセスにおける時間の向き」という視点で、可逆計算のメタファーによるデザインを考えてみる。
可逆であることとは異なるが、デザインにおいてフィードバック、あるいは双方向的な関係はさまざまな観点から議論されてきた。代表的な例として、以下のようなものが挙げられる。
- インタラクション(行為のフィードバック)
- リサイクル/再利用/再資源化(マテリアルのフィードバック)
- ユーザーやマーケットからの反応(社会のフィードバック)
- 存在論的デザイン(デザインすることのフィードバック)
可逆計算において、順方向の演算と逆方向の演算は全く同等の重みを持っていて、どちらかが優先されることは無い。フィードバックの場合、双方向的な関係がドライビング・フォースとなって、デザインオブジェクトは刻々と変化していくが、時間の向きは常に一定である。それに対して、可逆デザインは、いわばデザイン(プロセス)における「Undo」機能を有している。それはつまり、時々刻々変化するデザインオブジェクトの状態を時間を遡って元に戻したり、戻した後にまた別の向きに進めることができること、つまり「戻せるデザイン」である。そのもっとも単純な例は、以下のように状態\(a\)が、シーケンシャルに行き来できる状態である。この場合、それぞれの状態のスナップショットを保存しておけば、簡単に可逆なプロセスをつくることができる。

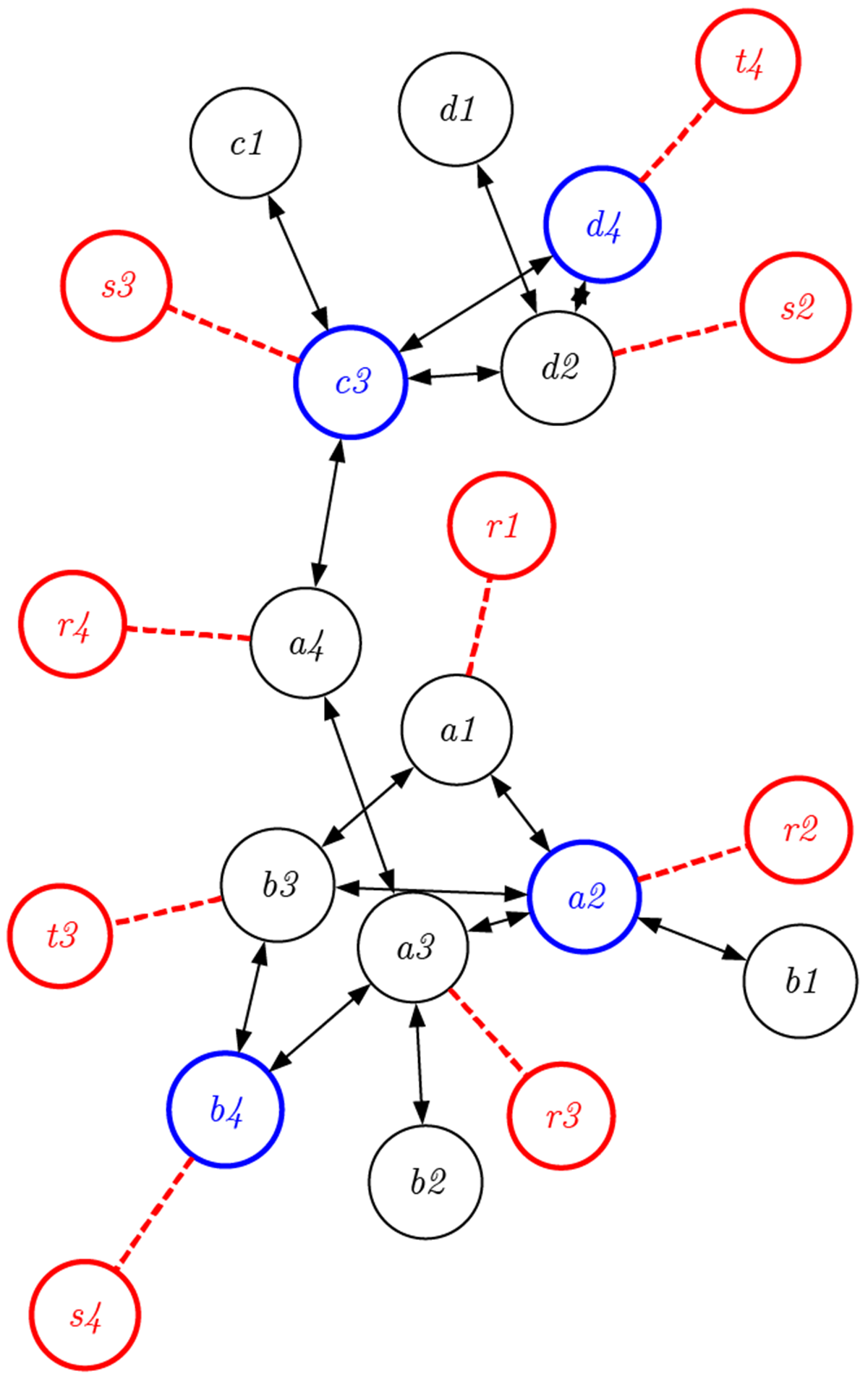
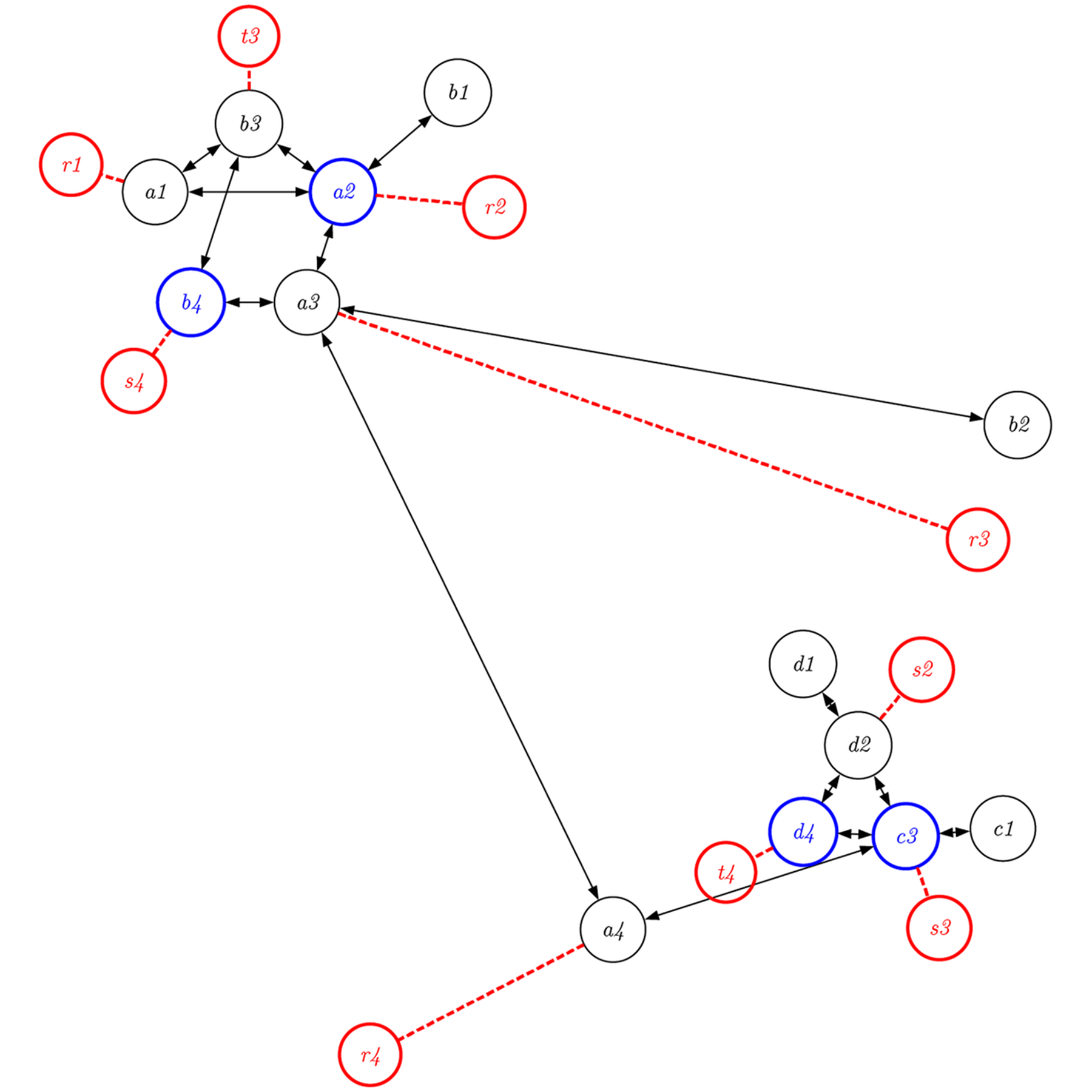
しかしながら、一般のデザインプロセスが、こうした一直線のシーケンシャルなものであることはない。複数のオブジェクト(例えば\(a, b, c, d\)の4つの対象)が、互いに相互作用したり、組み合わさりながら完成に向けて変化していく。
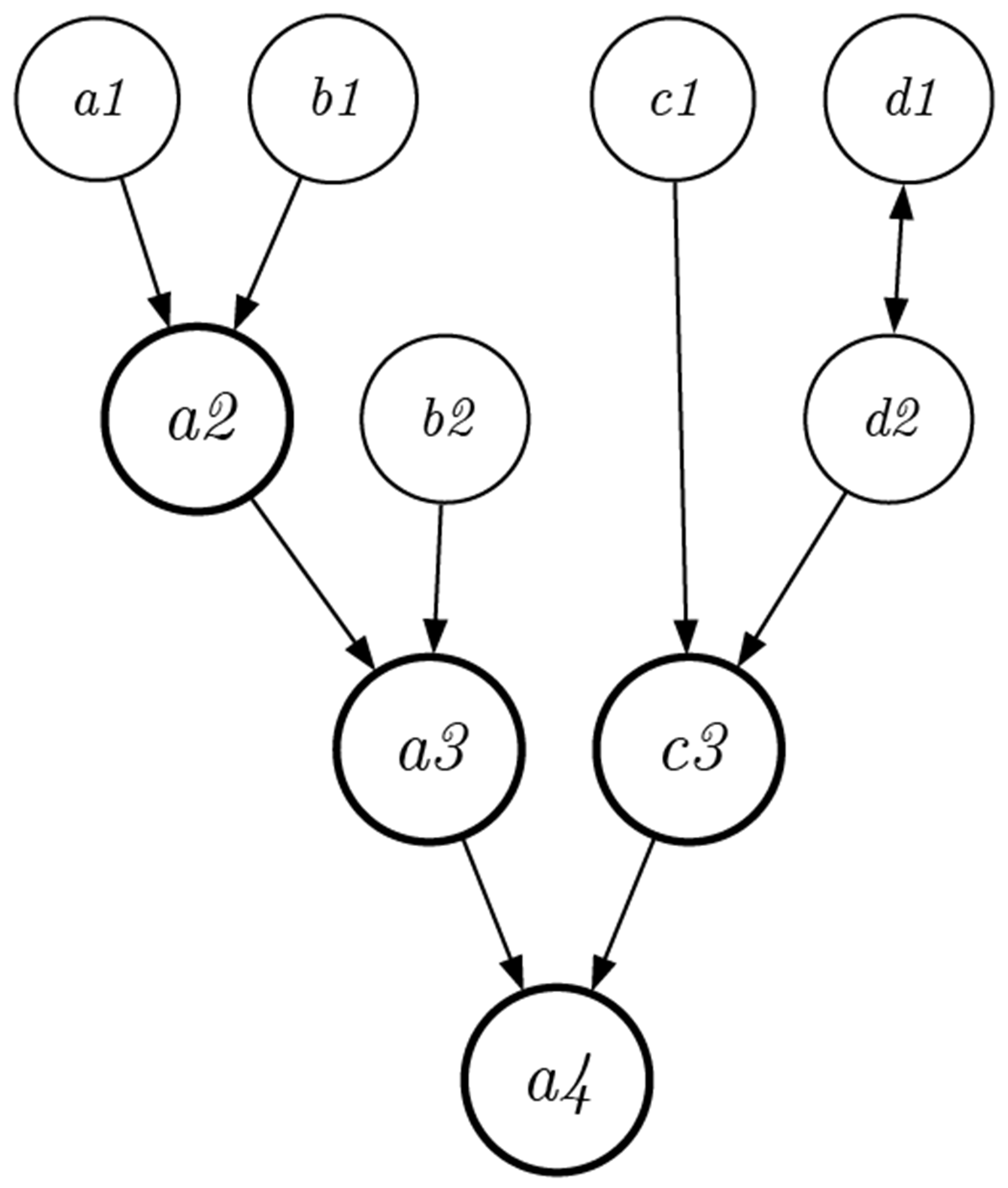
こうした(逆)ツリー型のプロセスの場合、例えば上図において太線のノード \(a \mathit 2, a \mathit 3, c \mathit 3, a \mathit 4\) に至る過程は、2つの入力に対して1つの出力しかないため、その過程は可逆にはならない(この図では \(d \mathit 1\) から \(d \mathit 2\) への変化のみ可逆である)。つまり一般のデザインプロセスは、非可逆の「覆水盆に返らず」の状況に置かれている。
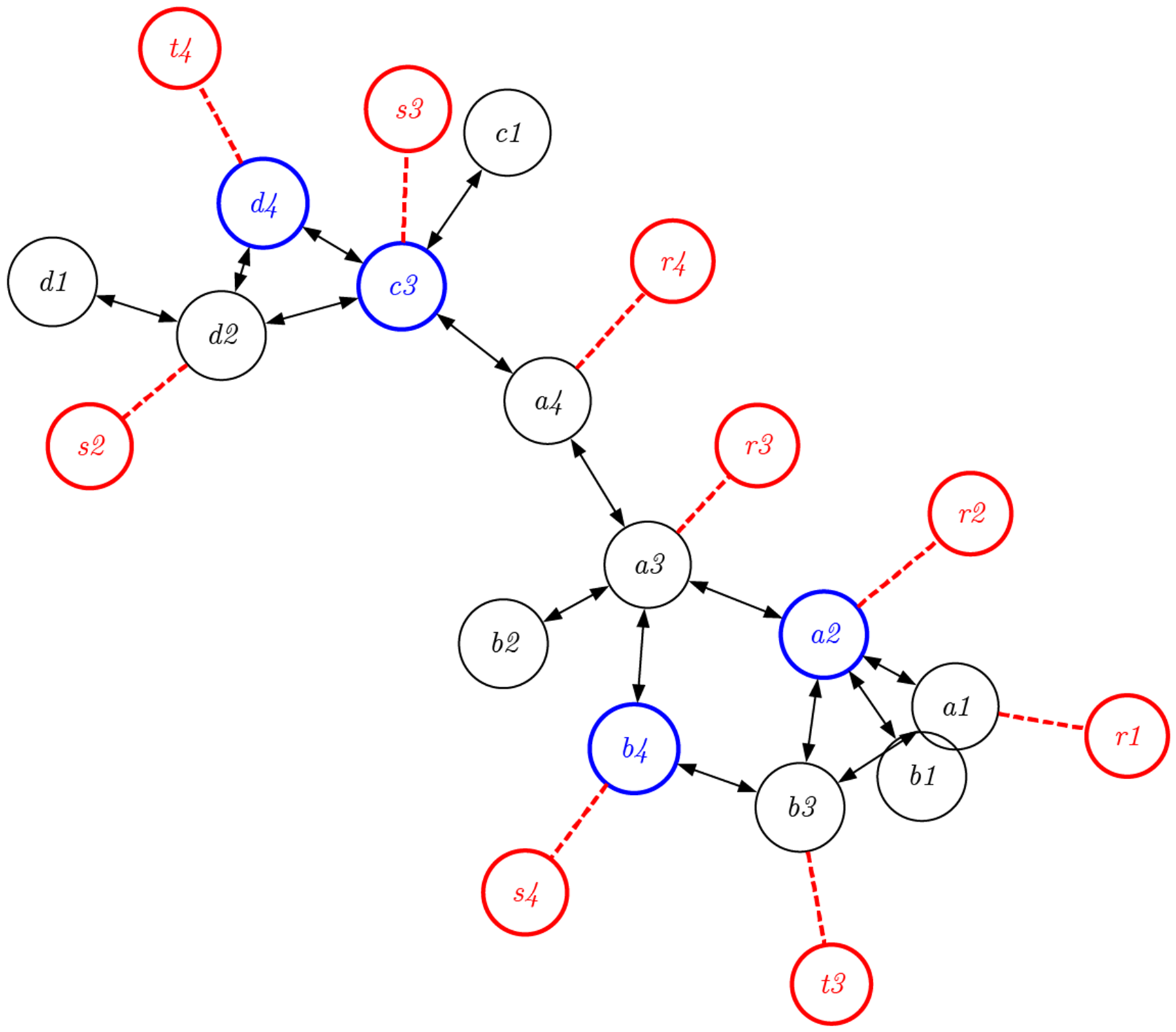
それでは、このプロセスを可逆にして、覆水を盆に返すことができる「戻せるデザイン」にするためにはどうすれば良いだろうか。ランダウアーの原理によれば、ものごとを蓄えておくためにリソースやエネルギーが必要とされるのではなく、不要なものを捨てたり、不要なことを忘れるときにリソースやエネルギーが使われる。何かを捨てることによって、デザインが非可逆になり、過去に戻れなくなる。捨てたことや忘れたことは二度と戻ってこない。
だとすれば、逆にデザインプロセスにおいて、不要なものを一切捨てなければ、そのデザインは可逆になるのではないか。
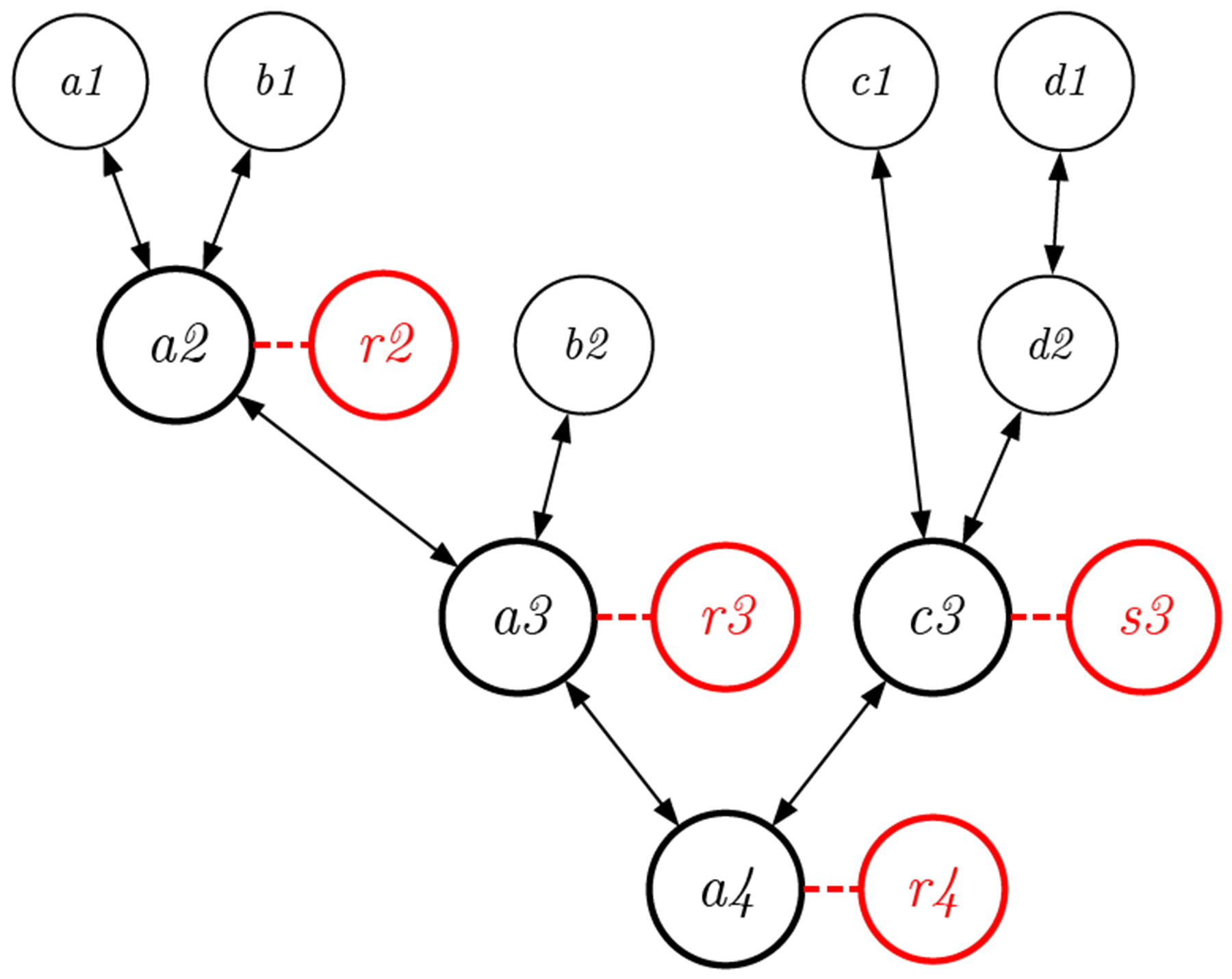
上図において、赤いノードで示されているものが、従来不要とされ、捨てられていたものに相当する。デザインプロセスにおいて、不要なものを捨てなければ、デザインプロセスの向きはすべて可逆になり得るはずだ。
近代デザインと生物の進化
こうしたデザインの可逆化の考えは、近代デザイン、特にシンプリシティーやミニマリズムの考え方とは、相容れない部分がある。例えば、作家であるだけでなく、パイロットでもあったサン=テグジュペリは、以下のような有名な言葉を残している※14。
In anything at all, perfection is finally attained not when there is no longer anything to add, but when there is no longer anything to take away, when a body has been stripped down to its nakedness.
何事においても、完成は、加えるものがなくなったときではなく、取り去るものがなくなったとき、つまり、身体が裸になったときにようやく達成される。
サン=テグジュペリ『星の王子さま』
「少ないほど良い(Less is more)」も、20世紀のデザイン業界においては、よく聞かれたフレーズだった。その起源は、建築家ミース・ファン・デル・ローエとされることが多いが、その考え方自体は、バウハウスを創設したヴァルター・グロピウスや、ル・コルビュジエの美学などにも通じていた。機能主義デザイナーのディーター・ラムズも「グッド・デザインの10の原則」の最後を、このような項目で締め括っている※15。
Good design is as little design as possible
Less, but better – because it concentrates on the essential aspects, and the products are not burdened with non-essentials.
Back to purity, back to simplicity.良いデザインとは、できるだけデザインをしないこと
「Less, but better」— より少なく、しかもより良く。それは、本質的な部分に集中するということ。それによって製品は、不要で過剰なデザインから開放される。
純粋で簡素、そこに立ち返ることだ。
ディーター・ラムズ「グッド・デザインの10の原則」
その一方で、人間のみならず、生物の進化とそこから生まれた身体は、こうした近代デザインのシンプルでエレガントなミニマリズムの対極にある。そこにあるのは、何度も何度も消しゴムと修正液で描き換えられた、ぼろぼろになった設計図の山である※16。
動物もヒトも、身体の歴史をたどってみると、実に面白い足跡が見えてきた。もともとはナメクジウオのような優れた設計図があったとして、それが大胆にも何度も描き直された挙句、ついには継ぎ接ぎだらけの形として、いまの時代に生きていることがよく分かる。積み重ねられた設計変更は、それ自体、かなり無理をした構造が身体のなかに隠されてきていることを思わせるが、ことそれはヒトに至って表に出てくる。
二足歩行という、ある意味とんでもない移動様式を生み出した私たちヒトは、そのために身体全体にわたって、設計図をたくさん描き換えなくてはならなかった。そうして得た最大の〝目玉〟は、巨大で飛び切り優秀な脳だったといえるだろう。だが、そうして作り上げたヒトの身体は、現代社会がヒトに求める特異な環境、たとえば、頭脳労働や晩婚化、異様な長寿や技術依存社会の発展の中で、悲鳴をあげつつあるというのが本当のところだ。
遠藤 秀紀『人体—失敗の進化史』
デザインに「完成」概念は必要か?
20世紀の近代デザインと生物の進化を比較したときに、まず大きく異なるのは「完成」という概念の有無だろう。先ほどのデザインプロセスのダイアグラムでも、それを(逆)ツリー型と呼んだように、最終的に何かひとつのアウトプットが完成することが暗黙のうちに仮定され、それをひとつのゴールとすると同時に、作家や作品、あるいは製品というオーソリティの基盤としがちだった。
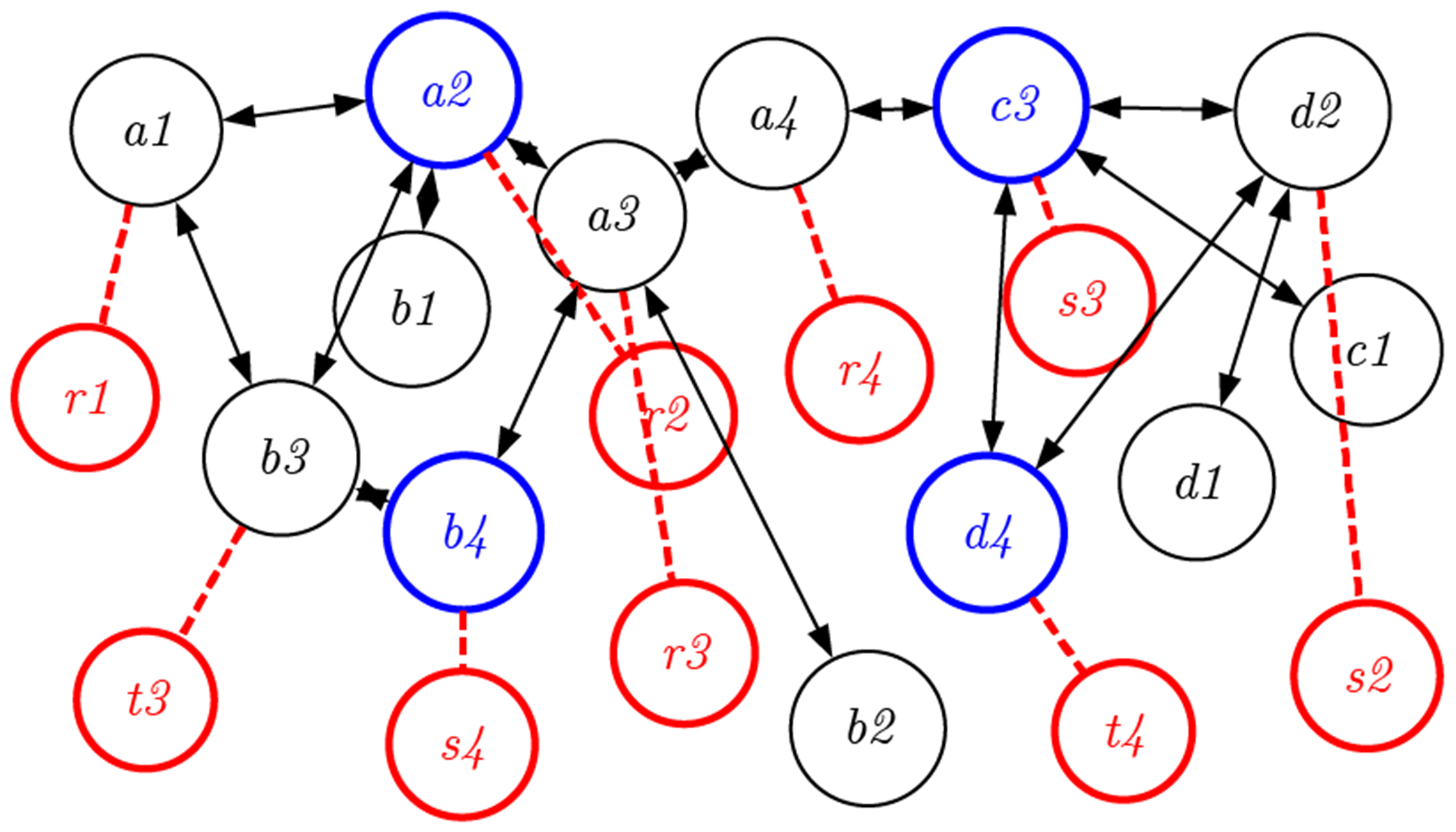
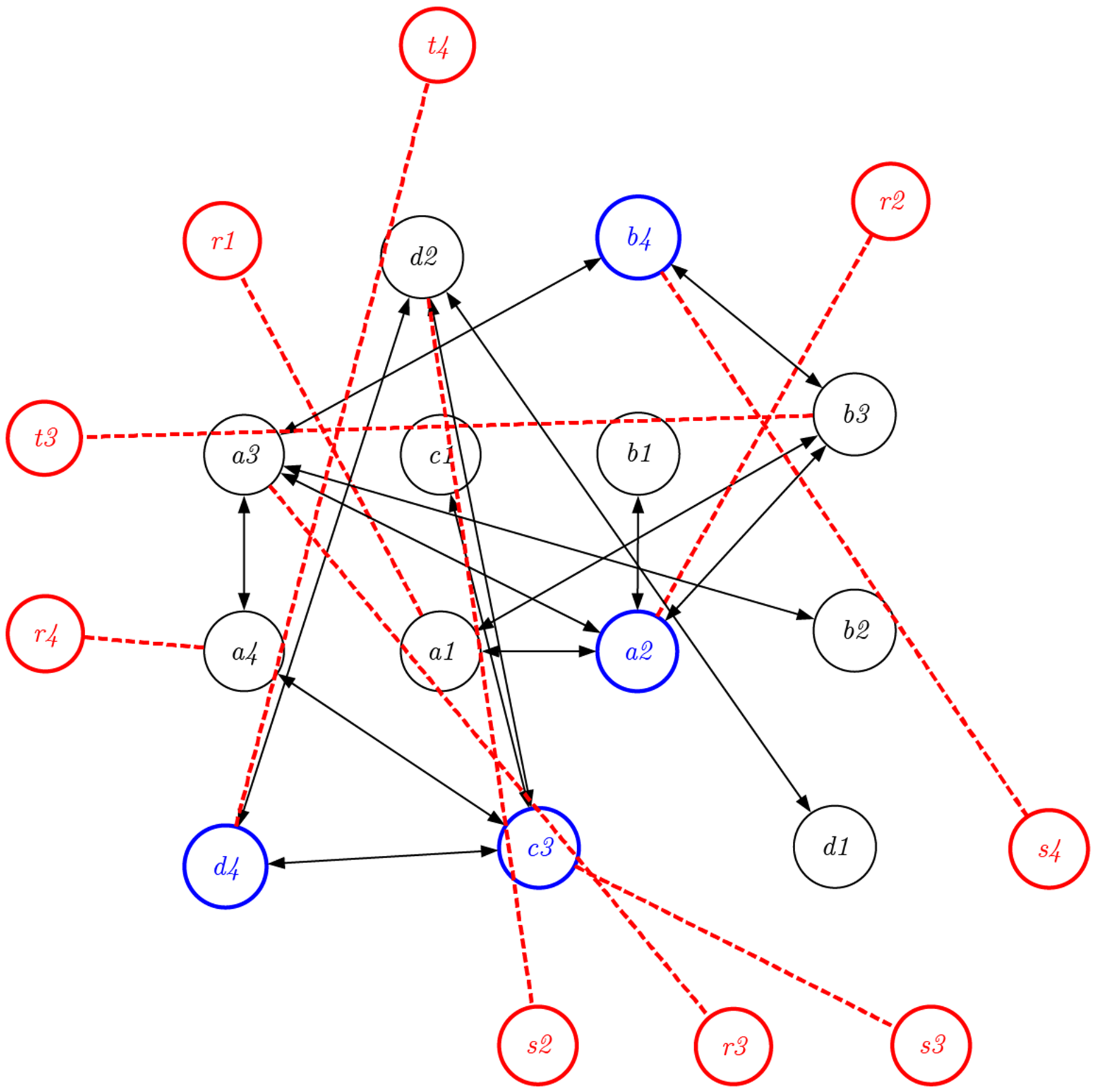
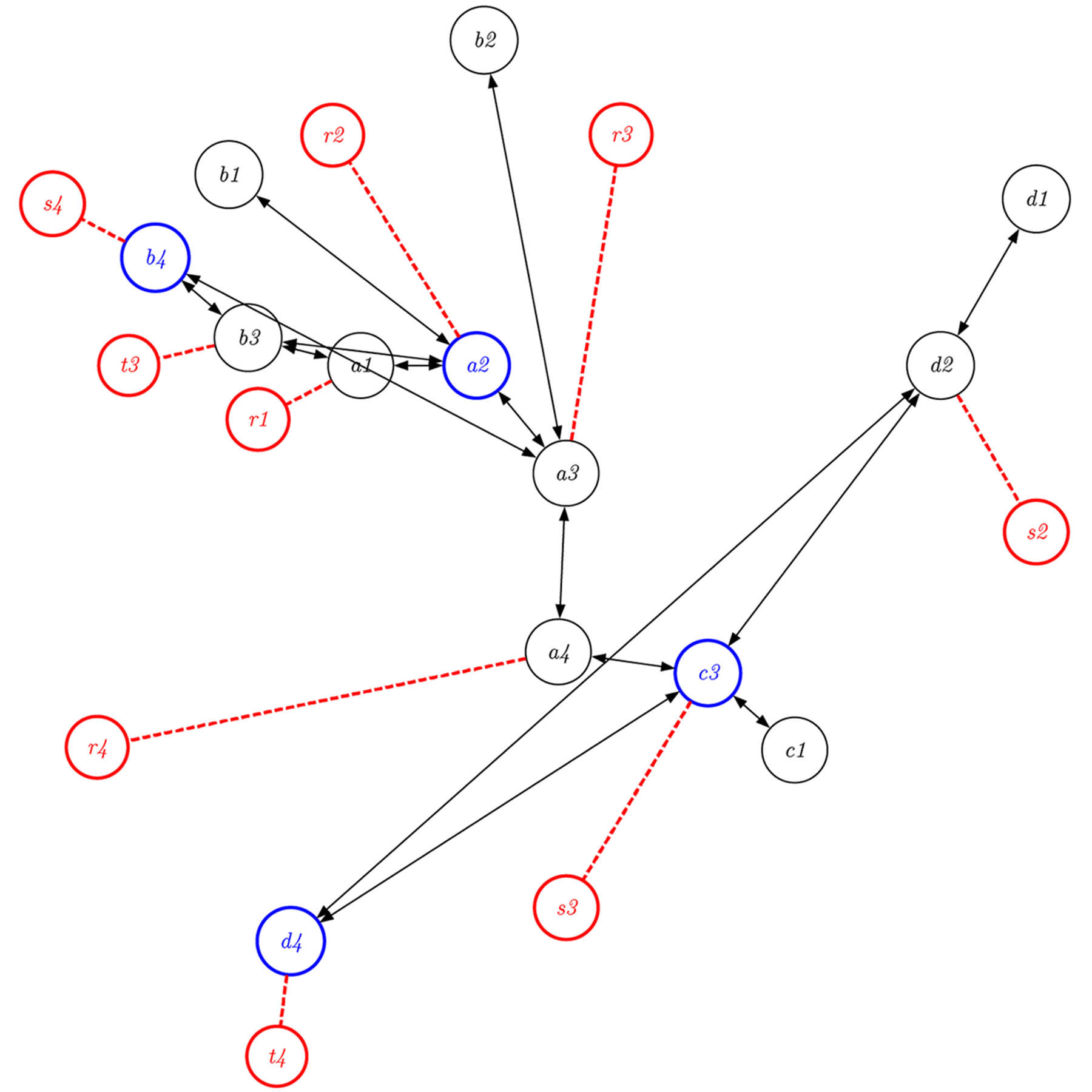
しかしながら、生物の進化には完成という概念はないし、人間の生活や社会の中でも、多くの人や物が変化し続け、複数の活動やプロセスが常に同時進行している。そうした状況の中では、デザインプロセスはツリー型というよりもネットワーク型である。
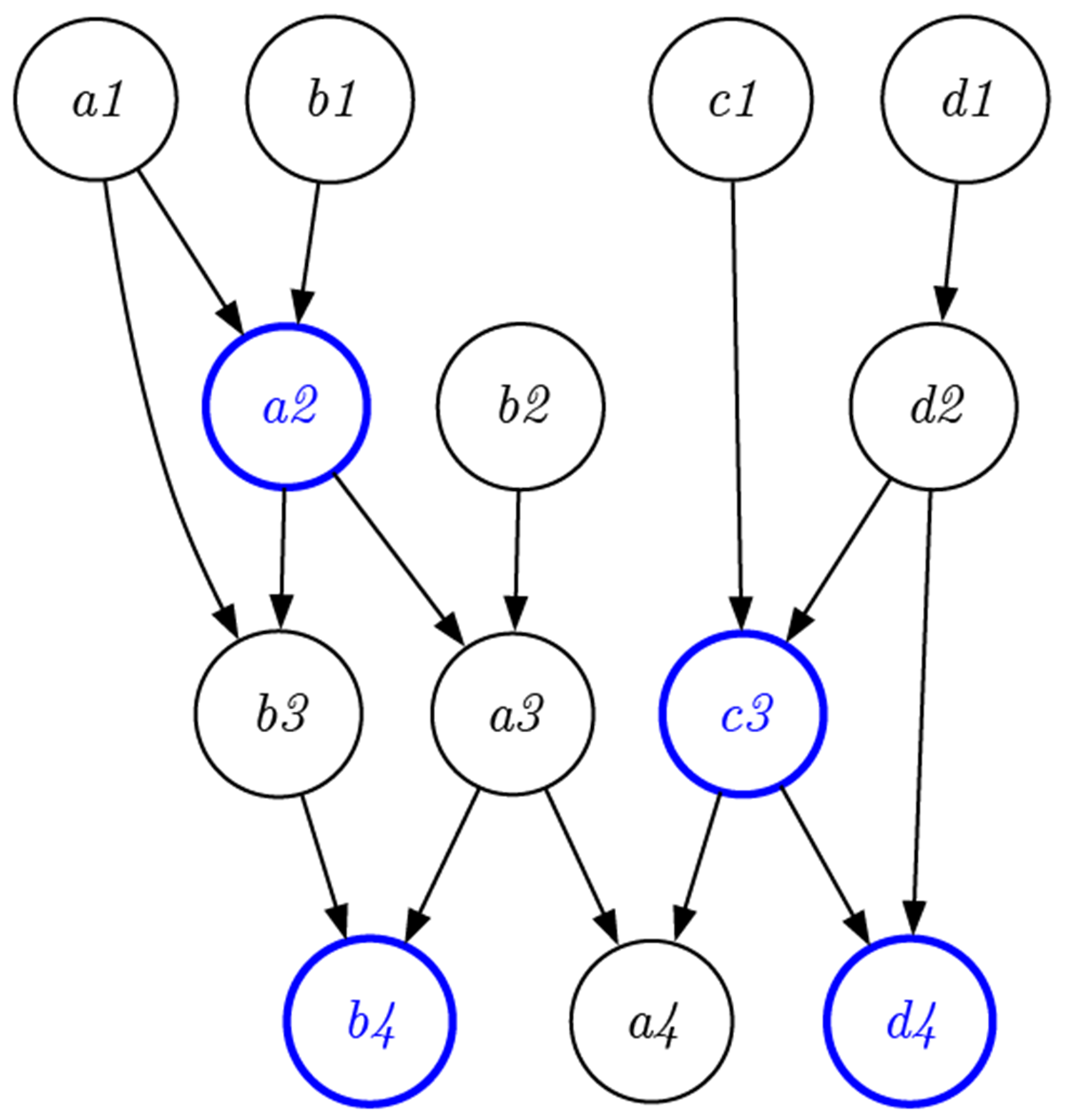
完成というひとつのゴールがあるわけではなく、さまざまなオブジェクトがときに使われたり(例えば青いノード)、そうでなかったりする。さらに、このプロセスを可逆にするために、先ほどのように、捨てないノード(赤いノード)を加える。
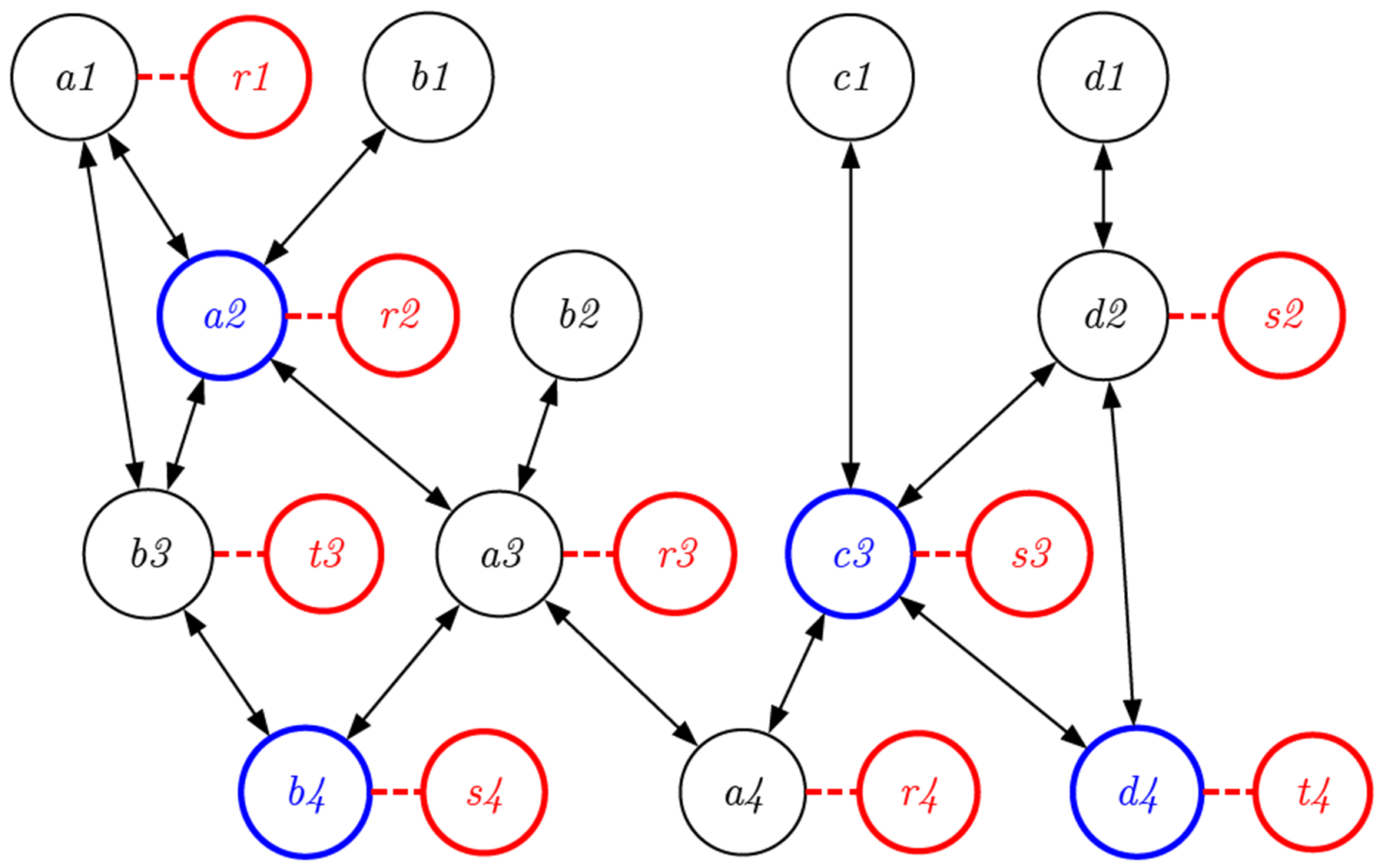
デザインにおける時間は上(過去)から下(未来)へと一方向に進んでいくわけではない。しかも時間軸は感覚的には決して直線ではなく、カーブしたり折れ曲がったりしている。さらに複数のプロセスで複数の時間が並列に進んだり戻ったりし、それらが分岐したり融合したりしていることを考えれば、この可逆ネットワークはさまざまな形で表現できる。
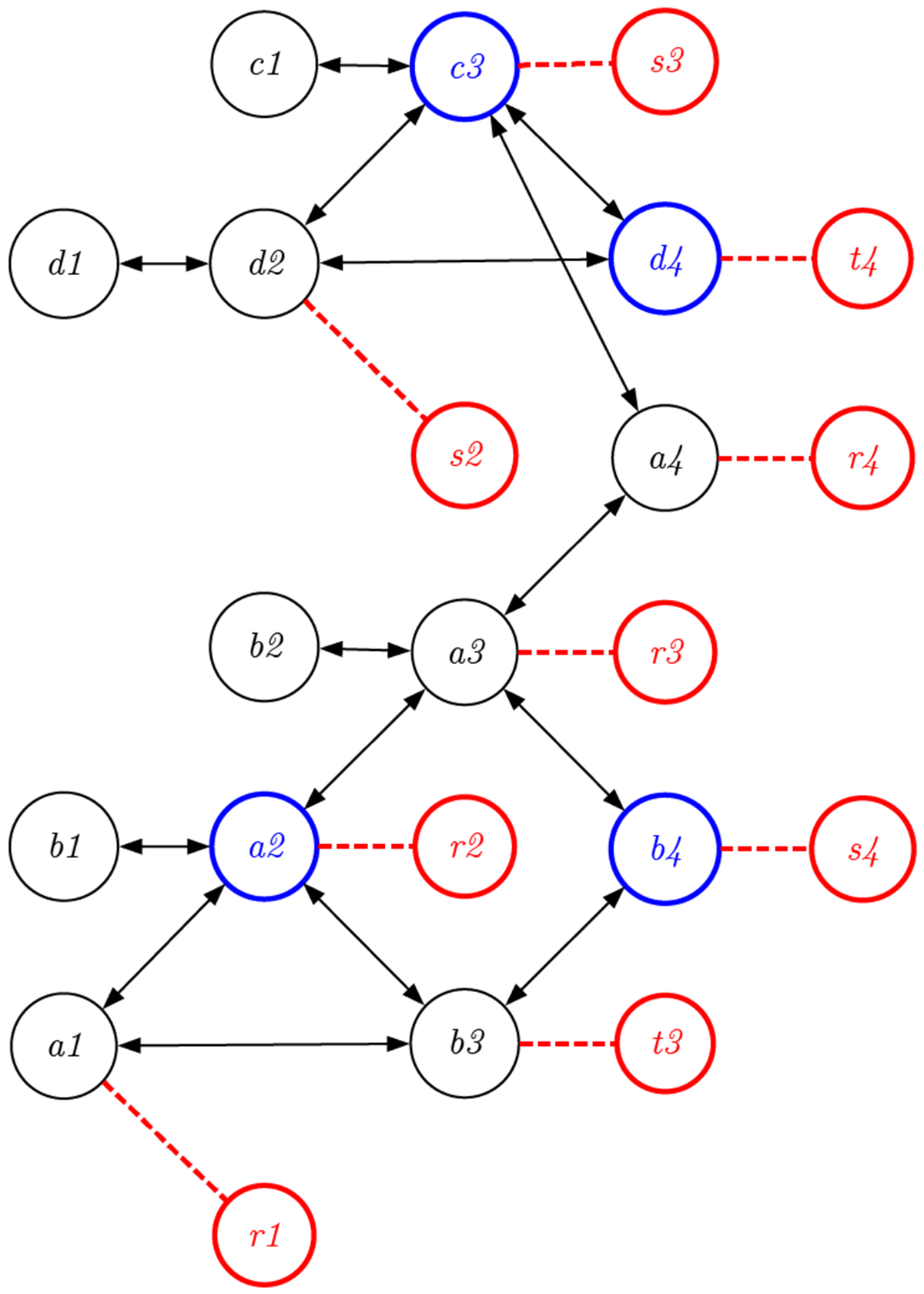
デザインのセル・オートマトンモデル
次に、1次元の(可逆)セル・オートマトンをデザインプロセスのモデルとして用いる。前述のように、近代デザインにおける完成概念は、取り去るものがなくなるまで不要で無駄な部分を削ぎ落とし、ものごとの本質的な部分を露わにすることだった。それは言い換えれば、もうUndoできないものに価値を見い出すことでもある。
ArrayPlot[
ResourceFunction["ReversibleCellularAutomaton"][
214, {{0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1,
0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1,
1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1,
1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1,
0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0}, {0, 0, 1, 1, 0, 0,
0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0,
1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1,
1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0,
0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0,
0, 1, 1, 1, 1, 0, 0} }, 50]]

しかし、それはあくまでデザイナーからみたデザインであり、いくらデザイナーがある状態を「完成」と見做したとしても、その使用によって、あるいはそれが置かれた状況の変化によって、「完成したもの」はすぐに解体、変容していく。
ArrayPlot[
ResourceFunction["ReversibleCellularAutomaton"][
214, {CenterArray[{1}, 100], CenterArray[{1}, 100]}, 50]]

だとすれば、つかの間の完成という結晶モデルよりも、常に変化し続ける、しかもどちらの方向にも向かうことができるデザイン流動体というモデルの方が、より適切なのではないだろうか?
ArrayPlot[
ResourceFunction["ReversibleCellularAutomaton"][
214, {RandomInteger[1, 100], RandomInteger[1, 100]}, 100]]

可逆デザインの日常イメージ
こうした、常に変化し続ける、しかも可逆なデザイン流動体のイメージな日常生活の中にもある。例えば、このようにスタックされたどこにでもある書類の山。そこには、それを積み上げた人の複雑な仕事や生活が反映されている。それと同時に、この山を共に仕事をしている人にとっては、すべてのものがあるべき場所にあり、暗黙の秩序と構造がある。


だから仕事をUndoできるようにするためには、この書類の山は片付けてはいけないし、それを一度片付けたら、たくさんの情報が捨て去られて、もう元には戻せない。これはコンピュータの中のさまざまなファイルについても同様である。コンピュータに保存しているデータも一度消したら二度と復元できない。だからデータも、それを可逆な状態にしておくためには、決して消去してはいけない。ファイルの中身だけでなく、ファイル間の関係であるディレクトリ構造も同様である。その考えをインターネット時空間全体に広げていけば、Internet ArchiveのWayback Machine※17が、いかに重要な役割を担っているかが、改めてよくわかる。
デザインにおける決定論と自由意志
こうしたデザインにおける可逆性は、「あらゆる出来事は、その出来事に先行する出来事のみによって決定している」という決定論、そして「人間は、外界に規定されずに、自発的に意志や行動を生み出す能力がある」という自由意志の問題につながっていく。ゲームデザイナーのクリス・クロフォードが2003年に著した『クロフォードのインタラクティブデザイン論(原題:The Art of Interactive Design)※18』には、「アンドゥによる可逆性」と題された、以下のような記述がある(下線は筆者による)※19。
コンピュータアプリケーションは自分の内部世界において時間の可逆性を認めています。その具体例が、至るところにある「アンドゥコマンド」という単純な救済メカニズムです。ご存じの通り、このコマンドはとても便利です。誤りを犯したら、アンドゥコマンドを選択するだけで誤りがパッと渭えます。しかし、ここでアンドゥコマンドを物謡りの語り手の観点から考えてみましょう。このコマンドは時間を逆行させ、誤りを犯す前の時点に戻してくれます。つまり、事実上、時間をさかのぽって決定を変更できるわけです。アンドゥの使用は、自分が自由意志を持っていることの証明になります。もしあなたが「君は頭の固い馬鹿野郎だ」と入力したならば、あなたがそのフレーズを人力すべく運命づけられていたのだと主張する人がいるかもしれません。しかし、あなたがその状態を元に戻して「君は誤解しているよ」と入力し直せば、運命を云々することはできないでしょう。時間の可逆性は自由意志の立証を可能にします。少なくとも、コンビュータプログラムという小世界に関する限りはそうです。ちなみに、自由意志を十分に働かせようとするならば、無限アンドゥ機能が重要になります。
クリス・クロフォード「アンドゥによる可逆性」
実際、先ほどのデザインのネットワークモデルのように、世界をさまざまな事象のネットワークであると考えれば、そこには可逆なものと、非可逆なものの両方がある。さらにその中には、人間が気づくものと、気づかないものの両方があるし、同様に人間が変えられるものと、変えられないものの両方がある。
そうした状況の中で、何を原因としてみるか、あるいは何を結果としてみるか、つまり因果関係という時間の向きは、極めて認知的である。実際、人間は気づいたもののうち、変えられそうなものごとを「原因」とみなすことが多く、同様に気づいたもののうち、変えられなさそうなものごとを「結果」とみなすことが多い。しかし本当は変えられるのに、そのことに気づいていないものごとも多く、それ以前に変えられないものごとには、そもそもあまり気づかない。
クロフォードがいうように、「ものごとをやり直すことで変えられる」ようにすることで、決定論や運命論から自由になれるとすれば、デザインプロセスを可逆な状態、つまり後戻りややり直しも含めて変更可能な状態にしておくということで、私たちは変えられるものを、変えられないと思い込んで諦めなくなるだけでなく、「自分たちで変えられるもの」に、より気づくようにもなるはずだ。
今日、私たちが喫緊に取り組まなければならないデザイン対象は、日常のちょっとしたTipsやローカルな生活ではなく、気候変動や社会格差、放射線やインターネットのように、私たちの身の回りに遍在していながら、巨大すぎて、それゆえ全貌が把握できず、間接的にしか知覚できないものである。そうした対象を、ティモシー・モートンは「ハイパーオブジェクト※20」と呼んだが、ハイパーオブジェクトの可逆性を問い直せば、そこに人間の自由意志を働かせることができるようになるかもしれない。
デザインとアクセシビリティ
この自由意志の問題はさらに、対象に対するアクセシビリティの問題へとつながっていく。前述の熱力学の第二法則、すなわちミクロレベルで可逆な物理現象が、マクロレベルでは不可逆になる問題を、沙川貴大と上田正仁は以下のように説明している※21。
伝統的なマクロ系の熱力学系においては、「マクロ/ミクロ」という区別と、「アクセス可能/不可能」という区別は、実質的に等価である。(中略)「アクセス可能/不可能」という観点からすると、不可逆な過程とは、アクセス可能な自由度からアクセス不可能な自由度にエネルギーが散逸するプロセスを意味している。しかし、もしもミクロな自由度にもアクセス出来れば、散逸したものを元の状態に戻すことが出来るのではないだろうか。
つまり、「アクセス可能/不可能」の境界を移動することは「可逆/不可逆」の境界を移動することでもあるのだ。
沙川貴大、上田正仁「Maxwellのデーモンと情報熱力学」
ここでは、物理現象の可逆/不可逆性が、対象へのアクセス可能/不可能性と結び付けられている。それをデザインプロセスへと敷衍すれば、可逆デザインを実践するということは、デザインの対象や過程をできるだけ「アクセス可能」にすることと同義になる。
例えば、ジェームズ・ローレンス・パウエルの『2084年報告書—地球温暖化の口述記録※22』の冒頭に、このようなやりとりがある。
「今日生きている私たちがぜひ尋ねたいのは、今世紀前半、まだ時間があるときに、なぜ当時の人々は地球温暖化を、少なくとも、遅らせる行動に出なかったのでしょうか?」
「十分な根拠はありませんでした。」
ジェームズ・ローレンス・パウエル『2084年報告書—地球温暖化の口述記録』
「根拠がない」ということは「地球温暖化が起こっていない」ということとは違う。クロフォードの例に倣えば、2084年に地球を今世紀前半の状態に戻して「地球温暖化が起こっている」とした行動を取り直すこと(Undo)ができないのであれば、地球温暖化に対応した行動を今すぐ取らなければ、人間自らが自由意志を放棄したことになる。そこに「無罪推定の原則※23」を適用することはできない。
この本以外にも、2050年の未来から、現在(2025年)の地球の行動を描くキム・スタンリー・ロビンスンの『未来省※24』のように、地球温暖化をテーマとして未来から現在を問いかけるフィクションがいくつか発表されている。ユートピアにせよ、ディストピアにせよ、現在から想像できる未来の物語を描く通常のSFとは異なり、こうした作品の特徴は、未来からみた過去としての現在における行動指針を描こうとする。それはアクセス可能な、つまり「可逆な過去としての現在」に向けたメッセージとして、未来に書かれた考古学の形をとる。
予言としてのデザイン
爾来、予言は現在の現実を変化させるためのひとつの方法であった。社会学者のロバート・マートンは、予言には、「今のままでは未来はこうなる」という現在を延長した予言によって、逆に現実を変化させ、予言自らが間違ったものとなる「自己破壊的予言」と、現在の状況からはあり得ない「意外な未来」を予言することによって現在を変化させ、最初は正しくないと思われた予言を実現させる「自己成就的予言」の2種類があることを示した※25。
人口過剰や水不足、気候変動といった解決が極めて困難な問題に取り組むために、デザインと議論を通じて人々の価値観や信念を変えようとするスペキュラティヴ・デザイン※26は、現在の状況からはあり得ない「意外な未来」を予言することによって(自己成就的)、今の現実を変化させようとする(自己破壊的)、未来をメディアとして用いた、もうひとつの「予言としてのデザイン」ということができる。
例えば、ユートピアとディストピアの中間に位置する近未来の物語を創造する研究主導型のデザイン・アートスタジオのNonhuman Nonsense※27は、矛盾したものや逆説的なもの、非現実なものごとを受け入れることで、人間以外のものと私たちの現在の関係を変化させることを目指している。

Youtube: Nonhuman Nonsense “Pink Chicken Project”
このNonhuman Nonsenseによるピンクチキンプロジェクト※28は、ある個体群において特定の遺伝子の保有率が増大する「ジーンドライブ※29」というバイオテクノロジーを使って、世界中のニワトリの骨と羽がピンク色になるように遺伝子組み換えを行うという提案である。2023年の世界のニワトリの飼育数は約240億羽で、世界の人口一人当たり3羽の鶏が飼われていることになる。このプロジェクトは、そんな鶏の骨が私たちの人新世の現在を象徴するものであると捉え、そこに技術的介入を行えば、人類の地質学的痕跡をピンク色に変え、未来の化石記録を人為的に修正できることを提示する。
このプロジェクトの背景には、ジーンドライブという、ある生物種の遺伝子を一斉に変えることすらできる極めて強力な技術の合法化と規制について、政府、国際機関、企業、教育、NGO、科学界の代表者らが、国連で活発に議論しているという状況がある。
その議論は現在、マラリア、ジカ熱、チクングニア熱といった、蚊が媒介する病気と闘うという倫理的に最善のユースケースに集中している。しかし技術自体に善悪の区別があるわけではない。ピンクチキンプロジェクトは、ジーンドライブの別のユースケースの提示という予言をデザインすることで、現在の状況を変化させようとする。2018年11月、ピンクチキンプロジェクトは、この予言のみならず、エジプトのシャルム・エル・シェイクで開催された国連の生物多様性条約のCOP-14会議に実際に介入した。

未来のための過去
ユッカマウンテン放射性廃棄物処分場※30は、米国ネバダ州ユッカマウンテンに計画されていた、高レベル放射性廃棄物の埋設処分施設である。1987年、高レベル放射性廃棄物処分場の唯一の候補地に指定されたが、2009年にオバマ政権はこの計画中止を決定した。
候補地の決定に先立つ1981年、米国エネルギー省はベクテル社と共同で、人間干渉特別研究班(HITF: Human Interference Task Force)を立ち上げた。人類学者、核物理学者、行動科学者などの多分野の専門家で構成されたこのチームは、将来の人間が放射性廃棄物の隔離システムに意図せず侵入する可能性を減らす方法を見つけることを目的としていた。その成果としてのテクニカルレポート「高レベル放射性廃棄物の地層処分場に影響を及ぼす可能性のある、将来の人間活動の可能性の低減(Reducing the likelihood of future human activities that could affect geologic high-level waste repositories)※31」が、1984年5月1日に出版された。
放射性廃棄物を深い地層に処分することは、廃棄物から人間を物理的に隔離するための手段のひとつである。しかし未来の社会がどのような状態になっているかがわからないため、サイトマーカーや警告標識、一般的な情報やサイトの管理、バリアやカバーのような施設や装置によって、その危険を言語的、視覚的、装置的に伝える方法も必要となる。そこでHITFは、ストーンヘンジやエジプトのピラミッド、ナスカの地上絵のような古代遺跡を「歴史的な類似物」として参照しながら、人間の侵入に対して起こりうる問題に対処するための、効果的なコミュニケーションについての研究を進めた。これは今から見れば、壮大な時間スケールにおける、スペキュラティヴ・デザイン・プロジェクトともいえる。

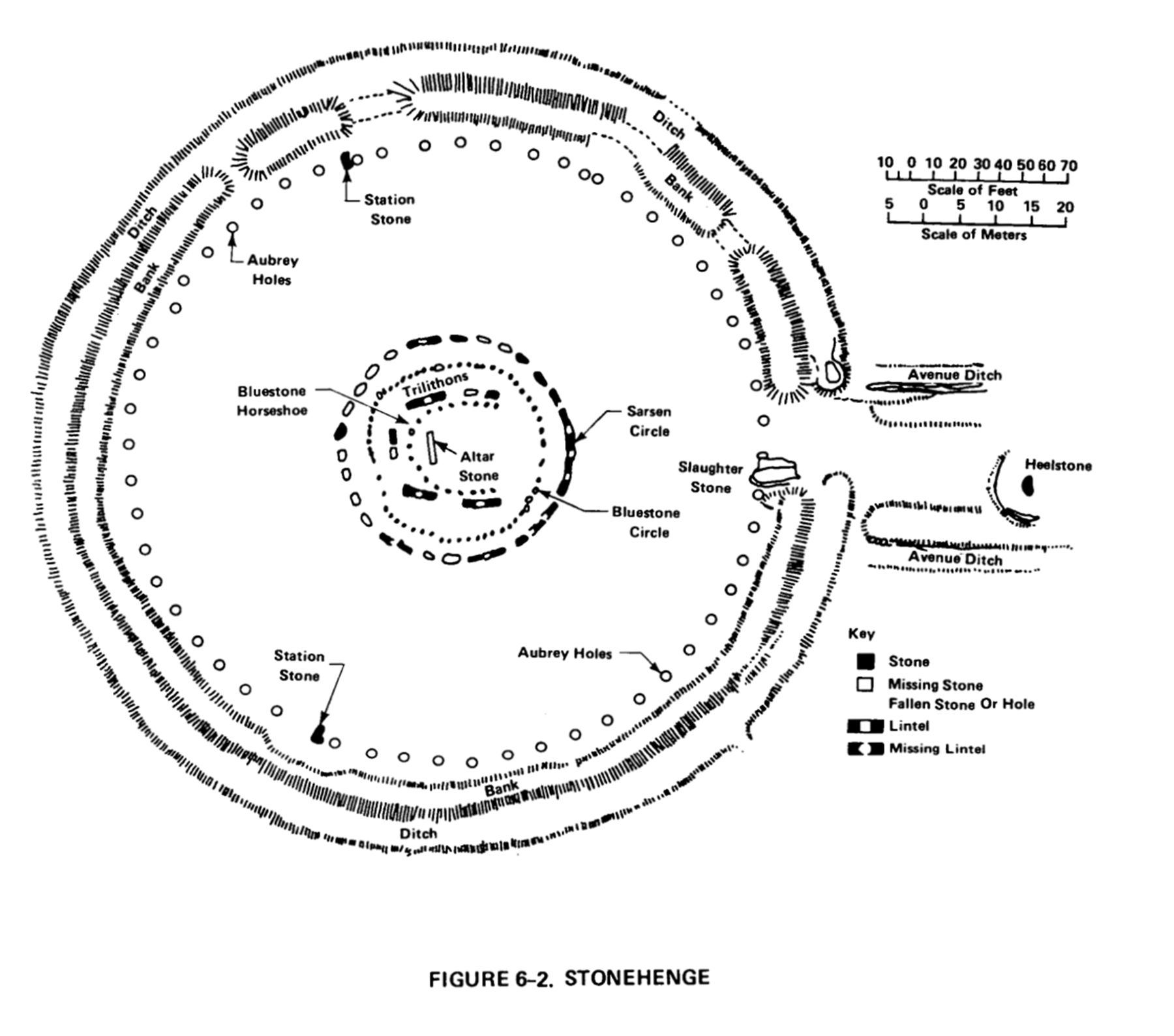
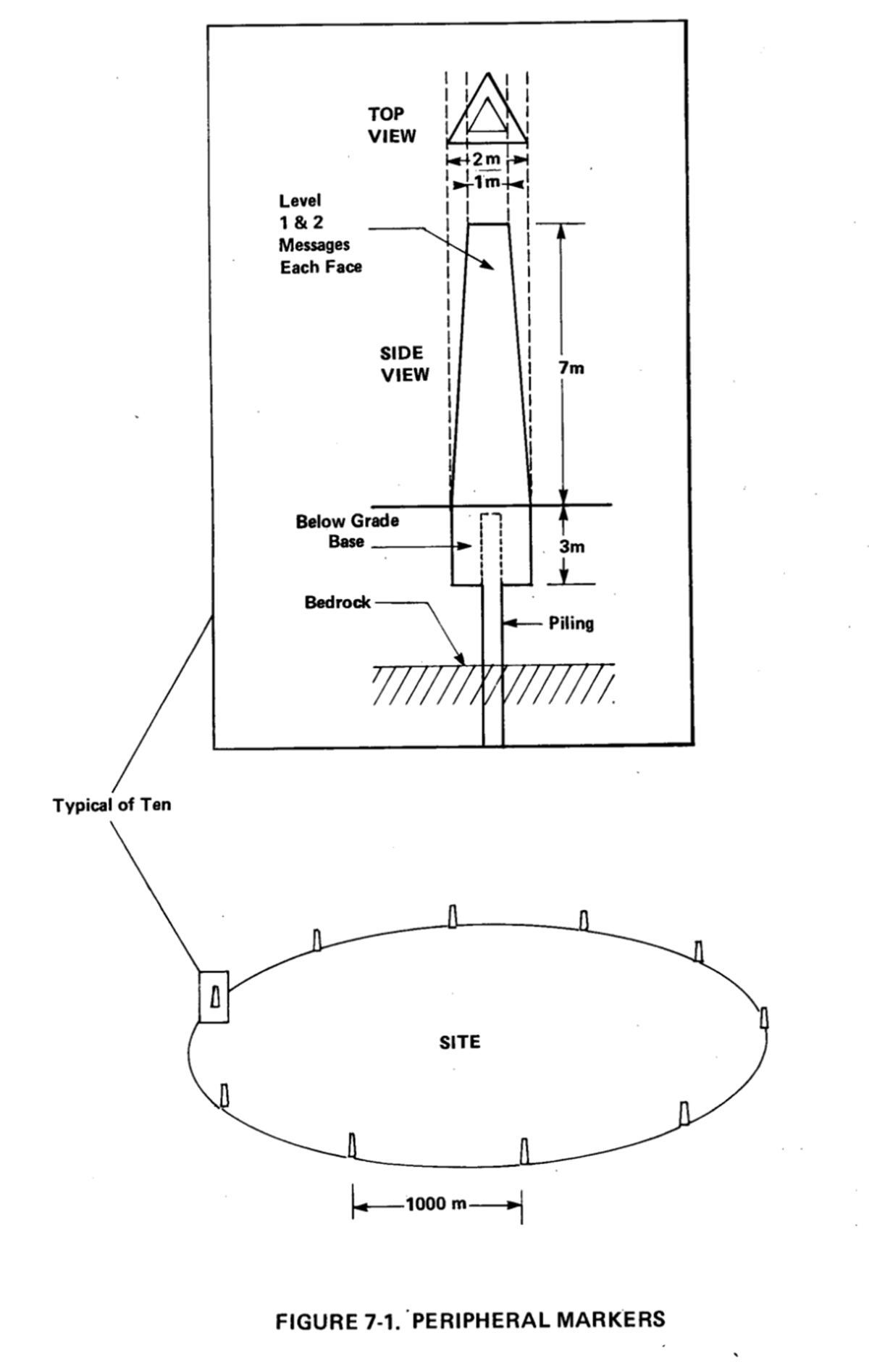
この報告書では、まず全体を統一するシンボルマークとして、以下の三角形と矢印からなる図像が設定された。
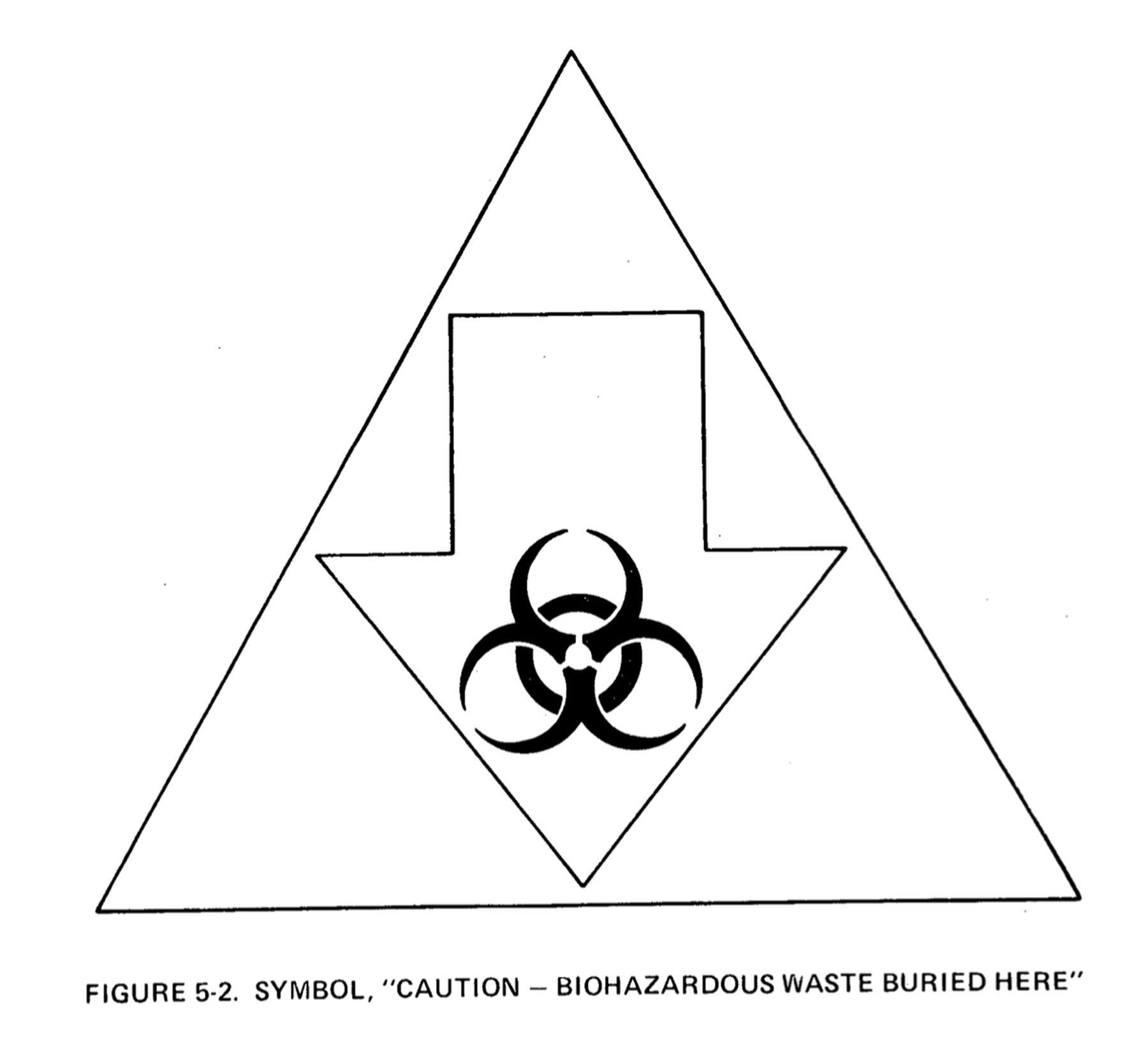
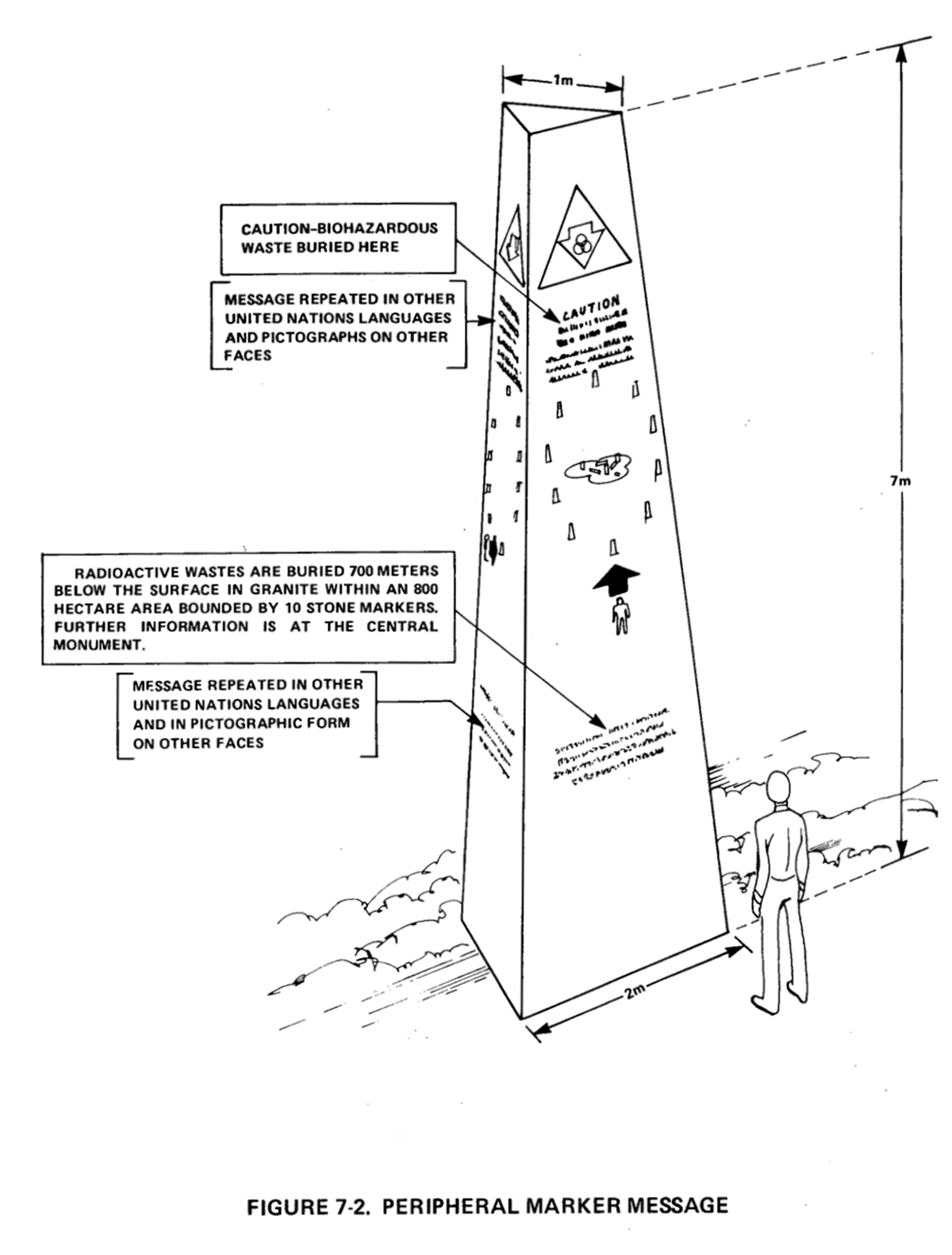
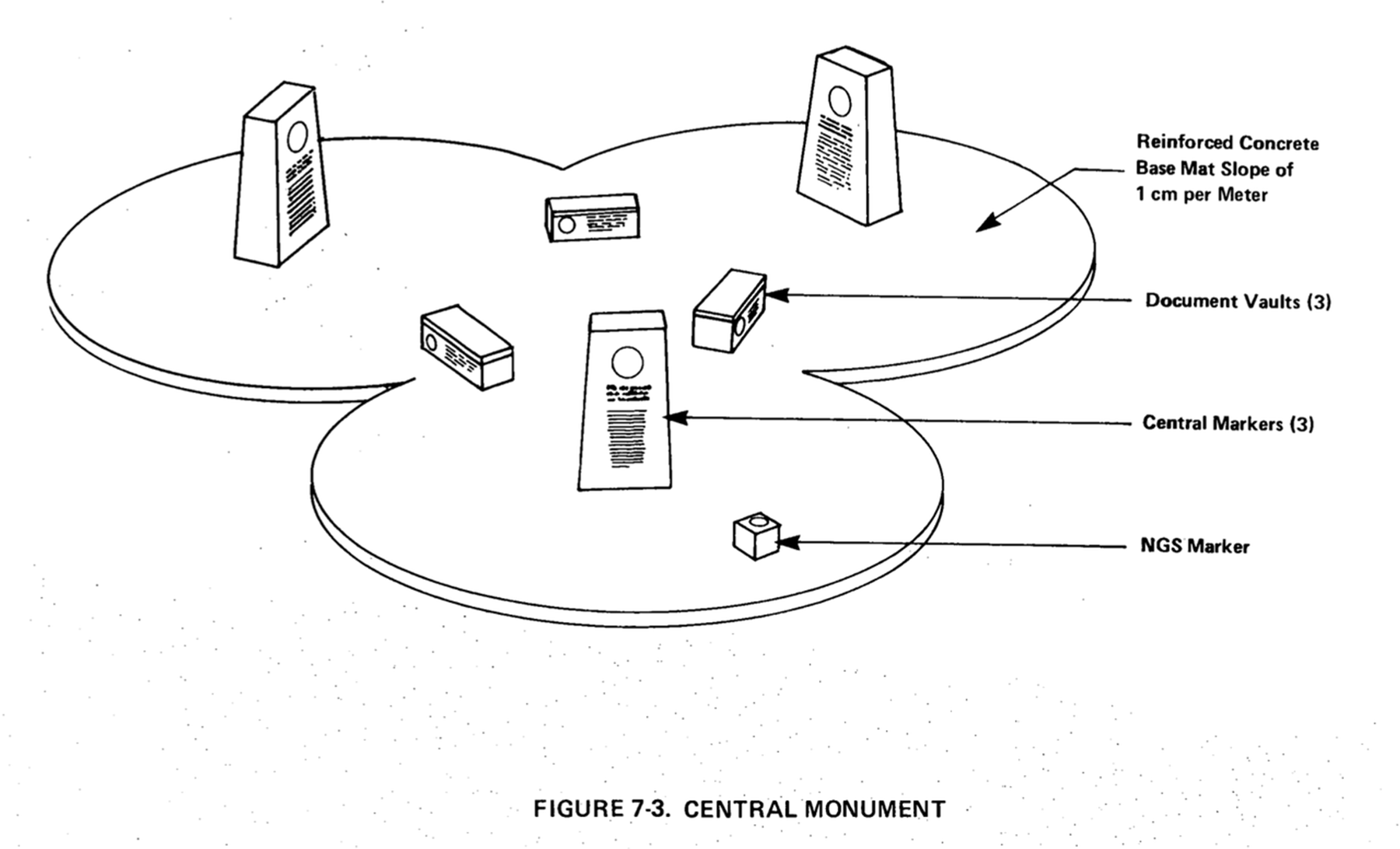
これを基本モチーフとして、以下のような廃棄場所を示す周辺マーカーとそこに描かれるメッセージ、さらに3つの大きなマーカーと3つの文書保管庫を三角形に配置した中央モニュメントがデザイン案として提示された。このマーカーは、断面がおよそ2×4メートルのやや先細りの四角柱状であり、文書保管庫は、外寸1.5×1.5×4メートルの花崗岩の中空ブロックで、厚さ30センチの底と側面、蓋がある。蓋の重量は約5トンで、簡単に持ち上げたり取り外したりすることはできない。
この案以外にも、中央モニュメントの別の案として、以下のようなより大型の、鉄筋コンクリートでつくられた一辺30m、高さ20mの三角形のピラミッド型のものが示された。サイズが大きくなることによって、モニュメントの視認性は高まるが、その寿命は花崗岩のモノリスやボックス程長くはないと考えられる。
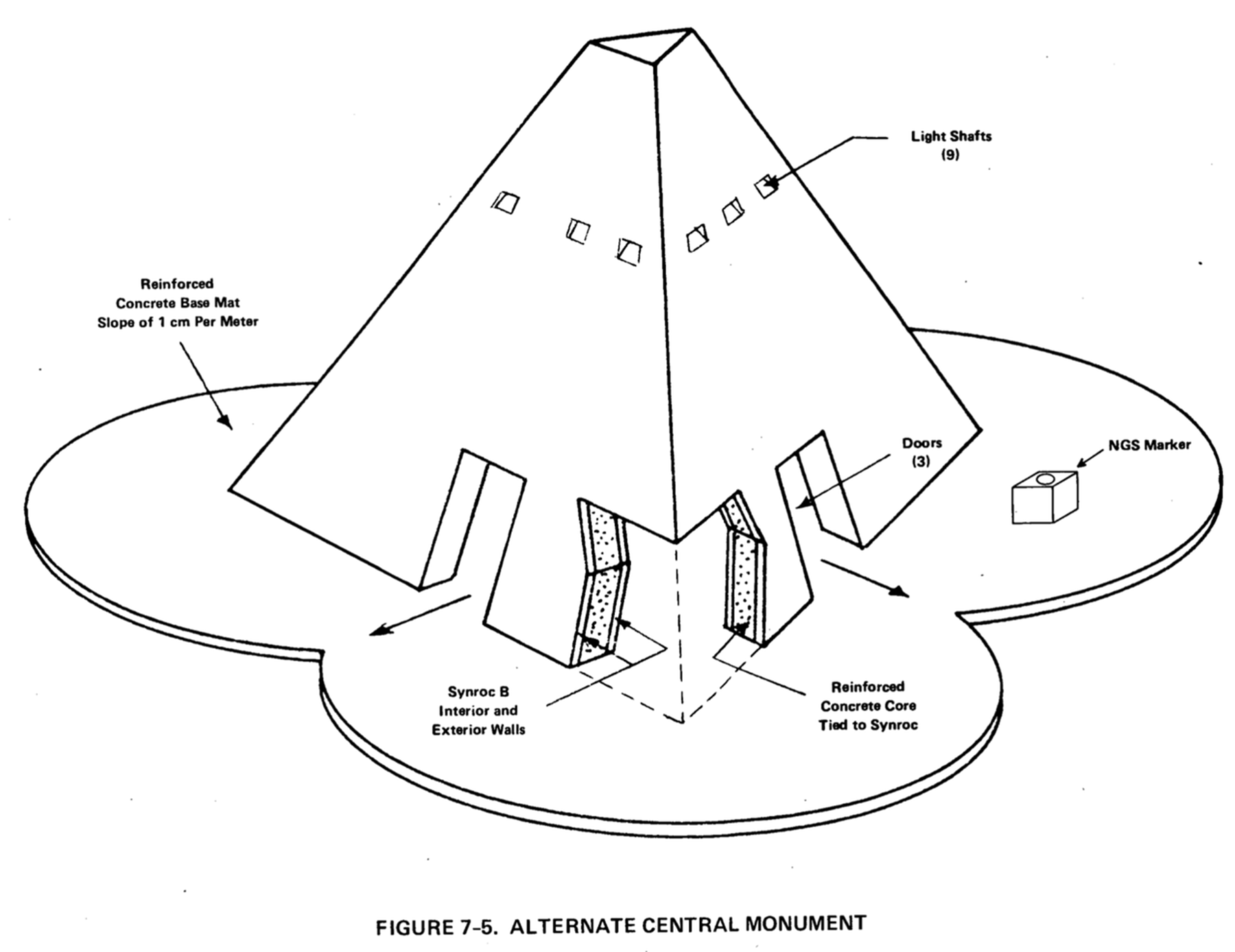
中央モニュメントのある広場は、一辺300mの三角形状で、その境界にはアスファルト混合物で15〜30cmの盛り土がある。その周辺は固有植生で安定化させている。
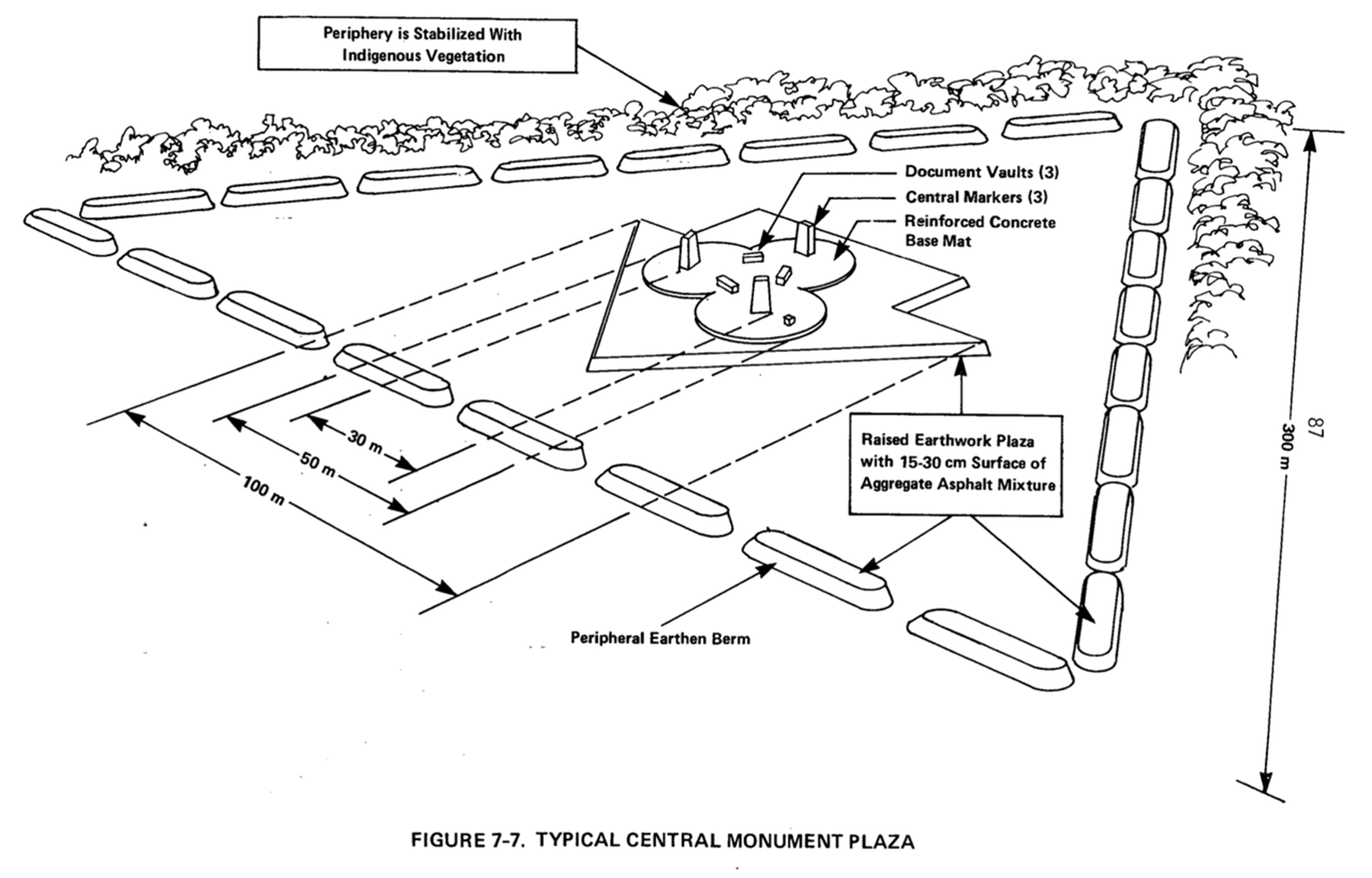
遠い未来を思索する
核廃棄物※32に含まれるプルトニウム239は2.4万年、ウラン238は45億年という、途方も無い半減期を持つ。こうした、人間の身体的な時間スケールを超えた物質の存在によって、それを今取り扱っている私たちは、1万年、10万年という遠い未来を否が応でも思索しなければならなくなった。そうした、文化的な連続性はなくとも、生物学的には連続性があるであろう人類の子孫とのコミュニケーションは、ユッカマウンテンのプロジェクトだけでなく、さまざまな議論が行われてきた。いずれの議論においても、核廃棄物の一番の危険は人間の侵入と自然災害にあると考えられ、未来の人間(あるいは生物学的基盤を共有する新たな知的生物)に、そこに危険があり侵入してはいけないことを伝えるためのメディアやメッセージ、さらには自然災害を避けるための場所と設置すべき装置が提案されてきた※33。
10万年後の人類に対して、今の人類はいかに責任を負うべきなのか。もちろん、そこまで長大でなくとも、今の地球環境は、私たち人間自身の行動が大きな要因となって、非可逆的な破壊に向かって進んでいる。しかし私たちは、数千年、数万年単位のタイムスケールを想像するどころか、わずか数10年後の地球や社会を想像し、それに責任をもって対応することすらできていない。
10万年後の人類に対して、今の人類はいかに責任を負うべきなのか。もちろん、そこまで長大でなくとも、今の地球環境は、私たち人間自身の行動が大きな要因となって、非可逆的な破壊に向かって進んでいる。しかし私たちは、数千年、数万年単位のタイムスケールを想像するどころか、わずか数10年後の地球や社会を想像し、それに責任をもって対応することすらできていない。
人類学者のヴィンセント・イアレンティは、「Deep Time Reckoning※34」で地球の遠い未来を想像するためのガイドを提供する。ここで「Reckoning」とは、天文観測による船位の推算を意味する航海用語である。私たちは、より長い「今」を生きることを学ぶことによって、イアレンティがいうところの「より熟練した深い時間の推算者(more skilled deep time reckoners)」になることができる。
イアレンティもフィンランドの放射性廃棄物最終処分場に着目した。しかし彼が特に着目したのは、「セーフティケース」と呼ばれる、最終処分の長期的な安全性に関する評価の信頼性を技術的、科学的に検証するための専門家チームである。「遠い未来のフィンランド」のシナリオをデザインするためには、異分野のモデルを接合するハイブリッドな方法論が必要になる。それは例えば、「地下水流動モデル」の出力を「放射性物質輸送モデル」に入力し、次にその結果が「生物圏評価モデルに」に入力されるといった、近視眼的な還元主義的思考とは対照的な、関係性から生まれるマルチスケールの学際的手段である。その時最も重要になるのは、異なる分野のモデルを接合した際に、たとえそこに不正確な仮定があったとしても、予測全体が無効にならないようにするための「戦略的冗長性」である。
セーフティーケースの作成チームは、未来学者というよりも、データを駆使する、トレーニングされた技術専門家集団であり、パターンの力を利用して遠い未来の詳細なシナリオや定量的なモデルを構築しようとする。チームは、SNSのような短い時間スケール上での情報の氾濫による「専門知識のデフレーション」という、今日のもうひとつの危機を乗り越えて、分野間の時間スケールの多様性を調整する「長期主義(long-termism)※35」の技術を教えてくれる。そうして、大きく異なるタイムスケールを自在に飛び回れるようになると、より洗練されたマルチスケール、マルチアングル、マルチパースペクティブな感覚が自然と身についてくる。人類の未来を消去する「人新世」を生き延びるためには、人々の心を「今」「現在」という狭い空間から解き放つ、深い時間のリテラシーに根ざした多次元的な思考と、長期的な視点に立つ人々のコミュニティの双方が、培われなければならない。
予言とアーカイヴ
遠い未来を思索するためには、現在の傾向から未来の状態を時間の流れの向きに沿って延長していく方法もあるが、逆に予言のように、まずゴールとしての「実現したい未来」あるいは「実現できない未来」「実現してはならない未来」を設定し、そこから時間を逆行していく方法もある。人間の「未来を構築する」ための前進的デザインにおける時間の向きを逆にすれば、それは人類が残した遺跡などのアーカイヴを通して人間の歴史を推測する、考古学の方法と重なってくる。
可逆計算のことを振り返れば、さまざまなものをできる限り評価選択せずに(つまり捨てずに)保存するアーカイヴがあれば、デザインに可逆性をもたらすことができる。
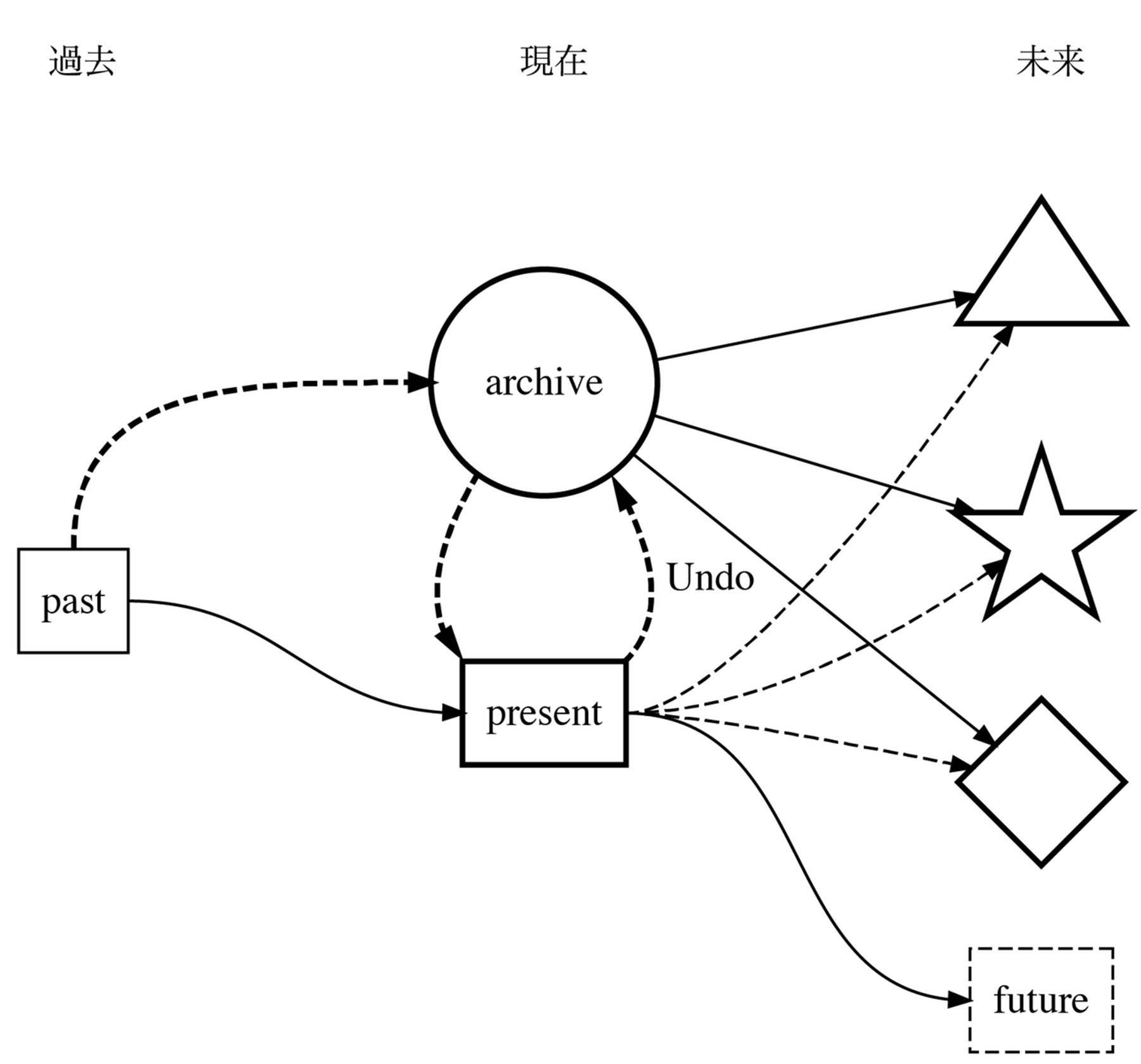
過去をなるべくそのまま保存し、堆積した過去そのものに対するアクセシビリティをもたらすアーカイヴは、いわば現在にUndo機能を実装するためのメディアである。過去へのアクセシビリティをもたらすアーカイヴによって、時間を(部分的にでも)可逆にすることができれば、そこからさまざまな現在のみならず、さまざまな未来をもたらすことができる。別の未来が、アーカイヴされた過去から再創造されるという意味で、未来は過去の中にある。さらにそれは、現状を肯定的に維持し、延長しようとする権威的なものごとを解体するためのツールにもなる。
一方で、未来から過去を逆算する予言、そしてスペキュラティヴ・デザインも、それを変更された現在によって別の未来を生み出すためのメディアだと考えれば、そのメカニズムはアーカイヴと双対の構造を持つ。つまり予言とは、未来を遡行する現在というアーカイヴによって、未来にUndo機能を実装するためのメディアである。
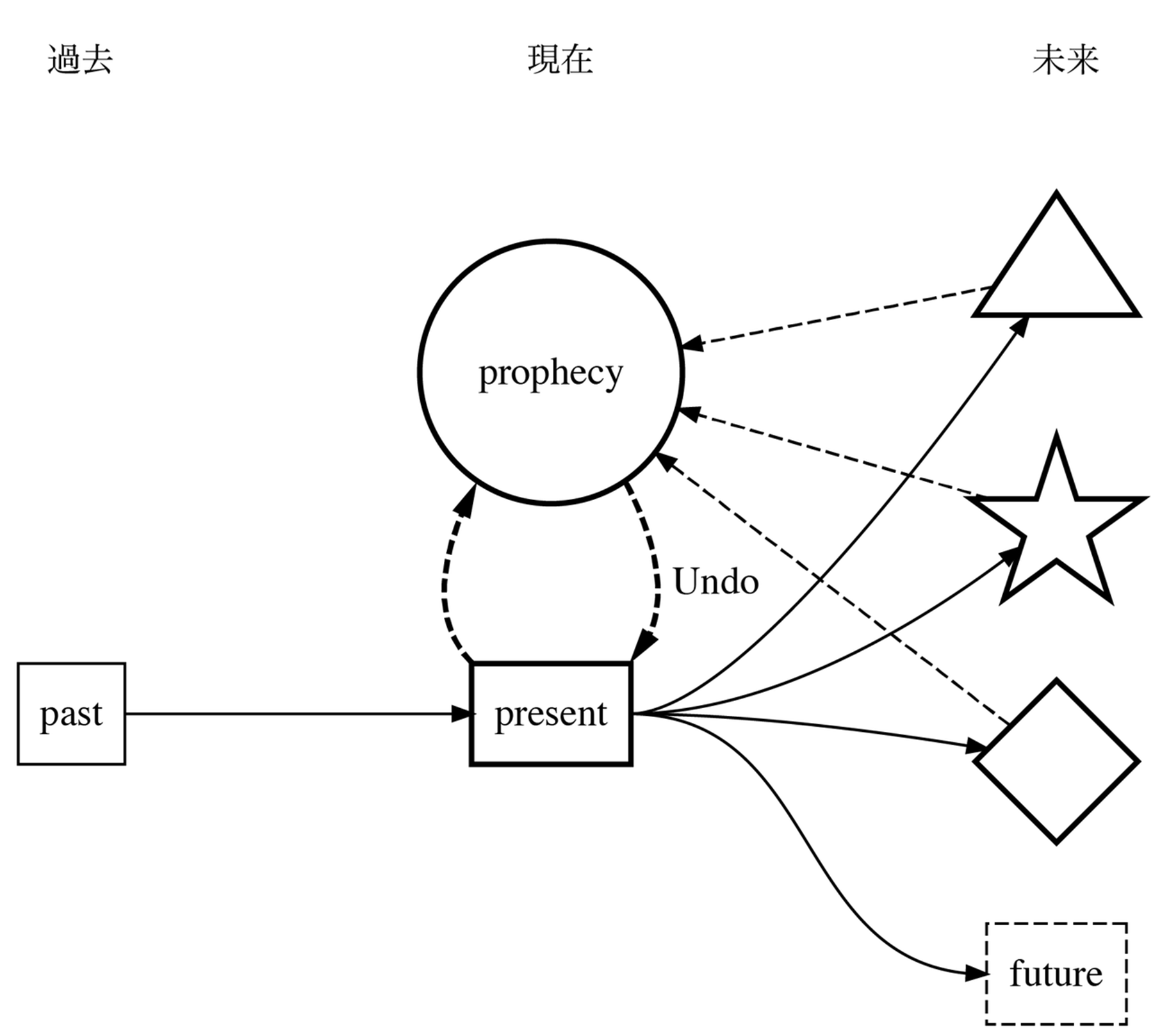
捨てないデザインによって可能になる可逆デザインは、人間の自由意志の証明でもある。未来へのアクセスを可能にする可逆性を、如何にして現在の社会に実装するかが、人新世の時代のデザインにとって、極めて重要なテーマになるだろう。

